3. Качественное исследование простейших моделей биопроцессов. Поведение переменных на фазовой плоскости вблизи состояния равновесия.

Простейшей математической модели соответствует одно дифференциальное уравнение первого порядка:

dx / dt = f (x);

Система в каждый момент времени характеризуется единственной величиной – значением переменной x в момент времени t. Состояния равновесия системы обозначим x (стационарная, или особая, точка). По определению, в этих почках (в состоянии равновесия) dx /dt_x = 0 и следовательно f(x) = dx/dt_x = 0.

Устойчивое состояние равновесия (стационарный режим функционирования): если при достаточно малом начальном отклонении от положения равновесия система никогда не уйдет далеко от него.

Система находится в неустойчивом состоянии: если систему вывести из равновесия, то она будет вести себя в соответствии с уравнением: dx / dt = f (x);

Для устойчивого состояния равновесия справедливо утверждение: если в момент времени t_o отклонение от состояния равновесия мало (|x(t_o) - x| < δ), то в любой последующий момент времени t > t_o отклонение системы от состояния равновесия будет также мало.

Состояние равновесия x устойчиво, если, задав сколь угодно малое положительное ε, всегда можно найти такое δ, что |x(t) - x| < ε для t_o ≤ t < + ∞, если |x(t_о) - x| < δ.

В практике используют аналитический метод исследования устойчивости стационарного состояния Пуанкаре и Ляпунова.

Рис. 1.1. Иллюстрация к определению устойчивости

Состояние равновесия является устойчивым (по критерию Ляпунова), если для любой заданной области допустимых отклонений от состояния равновесия (область ε) можно указать область δ(ε), окружающую состояние равновесия и обладающую тем свойством, что ни одно движение изображающей точки, начинающееся внутри δ, никогда не достигнет границы области е. Наоборот, состояние равновесия неустойчиво, если может быть указана такая область отклонений от состояния равновесия ε, для которой не существует области δ, окружающей состояние равновесия и области обладающей тем свойством, что ни одно движение, начинающееся внутри δ, никогда не достигнет границы ε.

Поведение переменных вблизи состояния равновесия может иметь разный характер (рис. 1.2). Переменные ζ, η – смещения относительно равновесия на фазовой плоскости

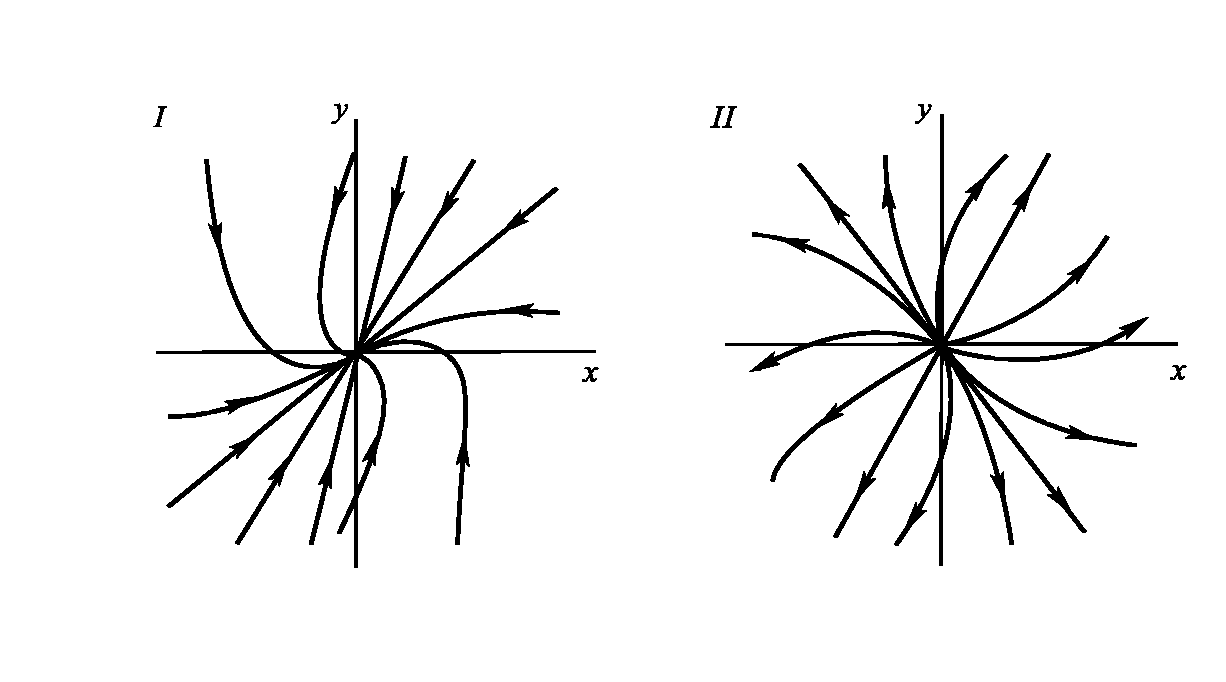
Рис. 1.2. Устойчивый и неустойчивый узлы на фазовой плоскости

Особая точка (х, у) представляет собой устойчивый узел (I): значения переменных ζ, η (отклонения от положения равновесия) со временем уменьшаются. Особая точка является неустойчивым узлом (II): значения ζ, η со временем увеличиваются.

Устойчивый узел – переход биосистемы от произвольного начального в стационарное состояние. Для многих биологических систем характерен «бесколебательный» переход от произвольного начального в стационарное состояние (модель «устойчивый узел»). Неустойчивый узел – отклонения от стационарного состояния со временем увеличиваются.

Неустойчивая точка типа «седло» на фазовой плоскости - за исключением особой точки все состояния переменных x и y удаляют систему от равновесия (рис. 1.3).

Рис. 1.3. Особая точка типа «седло» на фазовой плоскости xy

Особая точка типа «фокус» (рис. 1.4.): если колебания затухают, положение равновесия является устойчивым фокусом, если амплитуда колебаний нарастает, особая точка является неустойчивым фокусом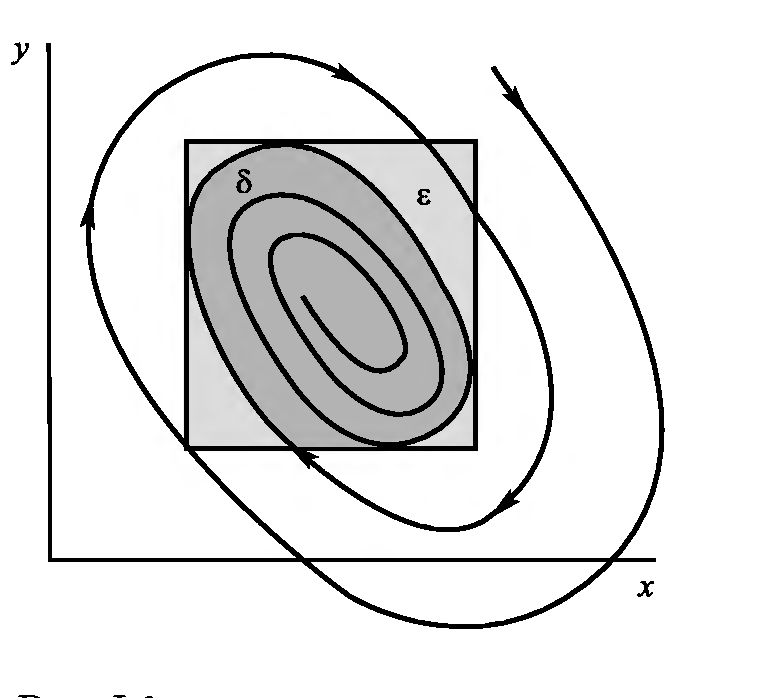

Рис. 1.4. Особая точка типа «фокус» на фазовой плоскости xy