Електростатичний потенціал.

Потенціал електричного поля - енергетична характеристика електричного поля; скалярна величина, що дорівнює відношенню потенційної енергії заряду в полі до величиною цього заряду. В СІ потенціал електричного поля вимірюється у вольтах.

У електростатиці електростатичний потенціал   визначається згідно із співвідношенням

,

де   - напруженість електричного поля.

Електростатичний потенціал визначений із точністю до довільної сталої. На практиці найчастіше за початок відліку служать потенціал заряду на нескінченості, або потенціал землі.

В системі одиниць СІ і на практиці вимірюється у вольтах

Теорема гауса.

Теорема Гауса була отримана в 1835 Карлом Фрідріхом Гаусом, який виходив із закону Кулона. В сучасній електродинаміці зазвичай застосовують протилежний підхід — за основу приймаються рівняння Максвела, одним із яких є теорема Гауса, а закон Кулона виводиться як наслідок.

Експериментальна перевірка справедливості закону Кулона з високою точністю набагато складніша від експериментальної перевірки теореми Гауса.

Теорема Гауса, як одне з основних рівнянь електродинаміки, загалом, справедлива і для середовища, у своїй основній формі. Наприклад, використовуючи систему СГС:

,

якщо під Q розуміти всі заряди, враховуючи мікроскопічні. Однак, присутність зовнішнього заряду призводить до перерозподілу мікроскопічних зарядів у речовині. Тому, якщо внести зовнішній заряд q в діелектрик, то деякі із мікроскопічних зарядів, змістившись, покинуть той об'єм, по якому проводиться інтегрування, інші - увійдуть у цей об'єм зовні - речовина поляризується.

Для врахування цих ефектів в електродинаміці суцільних середовищ усі заряди розділяються на вільні та зв'язані. Вільними вважаються ті заряди, які можна привнести зовні, зяряджаючи тіла, зв'язаними - електричні заряди електронів та ядер речовини, які в зовнішніх полях зміщуються, одні відносно інших, створюючи поляризацію:

,

де   - густина зв'язаних зарядів,   - густина вільних зарядів. Густина зв'язаних зарядів пов'язана з поляризацією:  .

Тоді теорема Гауса записується у вигляді

.

Вводячи вектор електричної індукції

,

отримуємо теорему Гауса для діелектричних середовищ:

,

або в диференціальній формі

.

Циркуляція вектора по контуру.

Циркуля́ція ве́кторного по́ля — криволінійний інтеграл по замкнутому контуру

.

де   — векторне поле.

Циркуляція потенційного поля дорівнює нулю.

Якщо F — деяке силове поле, тоді циркуляція цього поля по деякому довільному контуру Γ є роботою цього поля при переміщенні точки уздовж контура Г. Звідси безпосередньо слідує критерій потенційності поля: поле є потенційним, коли циркуляція його по довільному замкнутому контуру є нуль. Або ж, як випливає з формули Стокса, в будь-якій точці областіD ротор цього поля є нуль.

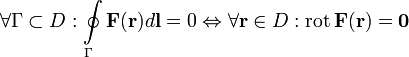
Теорема Стокса — одна із основних теорем диференціальної геометрії і математичного аналізу. Названа іменем ірландського фізика Джорджа Габріеля Стокса.

У термінах диференціальних форм теорема записується формулою

тобто інтеграл від зовнішнього диференціалу форми   по області   дорівнює інтегралу від цієї форми по границі області. У одновимірному випадку твердження збігається з формулою Ньютона—Лейбніца. Випадок інтегрування по двомірній області називається формулою Ґріна, по тривимірній області — формулою Остроградського.

Розглядається гладке (неперервно диференційовне) векторне поле   в  -мірному просторі, в якому задана система координат  . Якщо в цьому просторі заданий контур  (замкнута крива), на який натягнуто двомірний многовид  , то формула Стокса пов'язує циркуляцію векторного поля при обході всього контура з інтегралом від ротора цього поля по двомірному многовиду:

або в координатах:

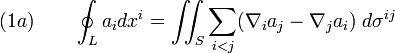
Окремо запишемо важливі часткові випадки цієї формули. Для випадку площини ( ) ця формула називається формулою Гріна, її прийнято записувати в таких історичних позначеннях (  — є частиною площини, обмеженою контуром):

Для фізики, особливо електородинаміки і гідродинаміки, важливою є формула Стокса в тривимірному просторі. Розглядаємо декартову систему координат   з правою орієнтацією. Ротор вектора   можна позначати вектором з координатами:

Орієнтація елементарної площадки задається одиничним вектором нормалі  . В цьому випадку формулу (1) можна записати через інтеграл по поверхні від скалярного добутку ротора і вектора нормалі:

Також, можна записати для тривимірного випадку формулу (1a) у виді суми трьох інтегралів по проекціям контура:

Спочатку обчислимо варіацію криволінійного інтеграла.

Розглянемо в  -мірному просторі криву  , (параметр   пробігає значення від нуля до одиниці  ), що сполучає дві точки   (при  ) і   (при  ). Будемо розглядати інтеграл вздовж кривої як функціонал  , що залежить від кривої (крапкою зверху позначатимемо похідну по параметру  ):

Тепер розглянемо близьку криву  , яка сполучає ті самі точки   і  . Варіація кривої   на кінцях перетворюється в нуль:  . Варіація функціонала дорівнює:

В першому інтегралі компоненти векторного поля   залежать від координати точки кривої, яка варіюється (при незмінному параметрі  ):

тому варіація векторного поля дорівнює:

В другому інтегралі проведемо інтегрування частинами, і врахуємо, що варіація кінців нашої кривої дорівнює нулю:

Зібравши ці два інтеграла до купи, одержуємо:

де введено позначення координат елементарної площадки - антисиметричного тензора паралелограма між кривою і бизькою до нею кривою:

Цей паралелограм побудований на векторах  . Дві вершини цього паралелограма ( ) лежать на оригінальній кривій. а дві інших ( ) на близькій кривій.

Оскільки тензор   антисиметричний, то формулу (7) ми можемо записати так:

Згадуючи означення коваріантної похідної (див. Диференціальна геометрія), і враховуючи симетрію символів Крістофеля по нижніх індексах, маємо:

Далі, в останньому інтегралі формули (8) доданки ненульові тільки тоді, коли індекси різні ( ), причому для кожного доданка в сумі існує рівний йому за величиною доданок з переставленими індексами. Отже ми можемо залишити в сумі тільки половину доданків з неповторними парами індексів, і одночасно прибрати множник  .

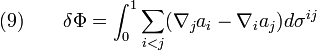
Тепер, маючи формулу (9) для варіації криволінійного інтеграла, уже легко доводити теорему Стокса. На замкнутому контурі   візьмемо дві точки (не обовязково різні, як це буде слідувати з подальших міркувань)   і  . Контур розіб'ється на дві різні криві   i  , що сполучають ці точки. Виберемо напрям на обох кривих від точки   до точки  . Тоді символічно можна записати:

і контурний інтеграл можна записати у вигляді різниці.

Тепер розглянемо двомірний многовид  , натягнутий на даний контур. Ми можемо розглядати плавну деформацію кривої на  , почавши з кривої  , і закінчуючи кривою   (проміжні положення деформованої кривої нагадують густий пучок меридіанів, що сполучають Північний і Південний полюси на карті Східної чи Західної півкулі Землі). Різницю функціоналів у формулі (10) ми можемо записати у вигляді інтеграла за формулою Ньютона-Лейбніца:

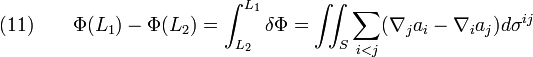
Порівняння формул (10) і (11) завершує доведення теореми Стокса.

СКАЛЯРНИЙ ПОТЕНЦІАЛ.

Скалярний потенціал векторного поля   —це скалярна функція    яка, що у всіх точках області визначення поля

де   означаєградиінт  . У фізиці зазвичай потенціалом називають величину, протилежну по знаку

ПОТІК ВЕКТОРА

Потік векторного поля через гіперповерхню — поверхневий інтеграл другого роду на поверхні  . За означенням

де   — векторне поле (чи вектор-функція векторного аргументу — точки простору),   — одиничний вектор додатної нормалі до поверхні (додатній напрям обирається для орієнтованої поверхі умовно, але однаково для всіх точок — тобто для диференційовної поверхні — так, щоб   був неперервним; для неорієнтованої поверхні це не важливо, оскільки потік через неї завжди дорівнює нулю),   — інфінітозимальний елемент поверхні. В фізиці іноді застосовують позначення

тоді потік записується у вигляді