2. Графический метод решения задачи линейного программирования

Если задача содержит только две переменные, а система ограничений задана в виде неравенств, то её можно решить графическим методом.

Графический метод решения ЗЛП состоит из следующих этапов.

1. Строится область допустимых решений (ОДР) ЗЛП.

2. Строится вектор-градиент целевой функции (вектор, координатами которого являются частные производные функции) с приложением в начале координат – .

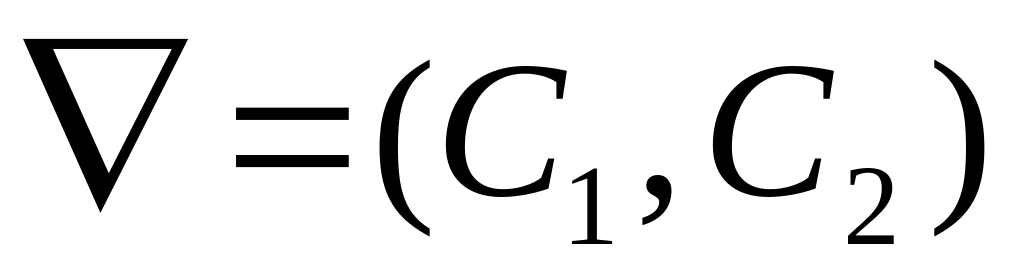3. Линия уровня C₁x₁+C₂x₂ = а (а – постоянная величина) - прямая, перпендикулярная вектору–градиенту – передвигается в направлении этого вектора в случае максимизации f(x_1,x₂) до тех пор, пока не покинет пределов ОДР. Предельная точка (или точки) области при этом движении и является точкой максимума f(x_1,x₂).

4. Для нахождения ее координат достаточно решить систему из двух уравнений прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума. Значение f(x_1,x₂), найденное в полученной точке, является максимальным.

При минимизации f(x_1,x₂) линия уровня перемещается в направлении, противоположном вектору-градиенту. Если прямая при своем движении не покидает ОДР, то целевая функция f(x_1,x₂) не ограничена на максимум (в задаче максимизации) или минимум (в задаче минимизации).

Если линия уровня параллельна какой-либо прямой из ограничений задачи, то оптимальное значение целевой функции будет достигаться в любой точке этой прямой.

Пример. Найти максимальное значение функции f=2x₁ + 3x₂ при условиях

Построим область допустимых значений:

1) первое ограничение x_+3x_18; прямая x_+3x_=18 пересекает оси координат в точках 06180; неравенству соответствует полуплоскость, содержащая данную прямую и лежащая ниже неё (контрольная точка 000+3*0<18 принадлежит полуплоскости);

2) второе ограничение 2x_+x_16: прямая 2x_+x_=16 пересекает оси координат в точках 01680; неравенству соответствует полуплоскость, содержащая данную прямую и лежащая ниже неё (контрольная точка 002*0+ 0<16 принадлежит полуплоскости);

3) неравенству x_5 соответствует полуплоскость, содержащая прямую x_=5 и лежащая ниже неё.

4) x₁0правее ОX_;

5) x₂0выше ОX₁.

Вектор-градиент имеет координаты .

Построим линии уровня 2x_+ 3x_ = а. При а =0 получим прямую 2x_+3x_ =0, проходящую через начало координат, перпендикулярно вектору-градиенту. Так как задача на максимум, то передвигаем линию уровня в направлении градиента. Предельной точкой (последней из области допустимых решений, с которой соприкасается линия уровня) является точка С. Значит, в ней достигается максимум функции f (рис. 1).

Найдём её координаты. Для этого решим систему, составленную из уравнений прямых пересекающихся в точке С (I и II):

Таким образом, получим x_6, x₂4, f_max 2*6+3*4=24.

Р ис. 1.

3. Нахождение решения задачи линейного программирования

Для решения ЗЛП существует универсальный метод – метод последовательного улучшения плана или симплекс-метод, который состоит из двух вычислительных процедур: симплекс-метода с естественным базисом и симплекс-метода с искусственным базисом (М-метод).

Выбор конкретной вычислительной процедуры осуществляется после приведения исходной ЗЛП к каноническому виду.

Для применения симплекс-метода с естественным базисом ЗЛП должна содержать единичную подматрицу размером mxm – в этом случае очевиден начальный опорный план.

Исследование опорного плана на оптимальность, а также дальнейший вычислительный процесс удобнее вести, если условия задачи и первоначальные данные записать в таблицу:

Базис	Сб	Р0	с1	с2	...	сm	cm+1	...	cn
			Р1	Р2	...	Рm	Рm+1	...	Рn
Р1	с1	b1	1	0	...	0	a1m+1	...	a1n
Р2	с2	b2	0	1	...	0	a2m+1	...	a2n
...	...	...	...	...		...	...	...
Рm	сm	bm	0	0	...	1	amm+1	...	amn
		F0	0	0		0	Δm+1		Δn

В первом столбце таблицы "Базис" записывают базисные векторы данного опорного плана. Во втором столбце - коэффициенты целевой функции (с₁, с_2,…, с_m) при базисных переменных (напомним, что в базис входят только векторы, образующую единичную подматрицу). В третьем столбце Р₀ - правая часть ограничений задачи (базисные компоненты плана). Таким образом, перемножая элементы второго столбца таблицы со столбцом Р₀, и суммируя эти произведения, мы получаем значение целевой функции (F₀=с₁*b₁ + с₂*b₂+…+ с_m*b_m).

Первая строка симплексной таблицы содержит коэффициенты целевой функции нашей задачи и остается неизменной на протяжении всего решения (с₁, с_2,…, с_m).

В центральной части таблицы записывают коэффициенты при неизвестных в ограничениях исходной задачи. При этом следует заметить, что коэффициенты при базисных переменных в ограничениях задачи составляют единичную подматрицу. Последнюю оценочную строку рассчитывают по формуле .

После заполнения таблицы исходный опорный план проверяют на оптимальность. Для этого просматривают элементы последней (оценочной) строки. Возможны три варианта:

1. Все оценки , значит на основании признака оптимальности получен оптимальный план.

2. для некоторого j, и все соответствующие этому индексу величины , значит целевая функция не ограничена сверху на множестве планов.

3. для некоторых индексов j, и для каждого такого j по крайней мере одно из чисел , значит можно перейти к новому опорному плану, при котором значение целевой функции увеличится.

Переход от одного опорного плана к другому осуществляется исключением из исходного базиса какого-нибудь из векторов и введением в него нового вектора. В качестве вводимого в базис вектора берётся один из векторов, для которых . Пусть это будет вектор Р_k.

Для определения вектора, подлежащего исключению из базиса находят . Тогда выполняется условие неотрицательности значений опорного плана. Пусть этот минимум достигается при i=r. Тогда из базиса исключают вектор Р_r, а число называют разрешающим элементом.

Элементы новой симплекс-таблицы получают методом Жордана-Гаусса по формулам:

для i = r;

.

Значения нового опорного плана рассчитываются по формулам:

для i = r;

.

Процесс решения продолжают либо до получения оптимального плана, либо до установления неограниченности целевой функции. Если среди оценок оптимального плана нулевые только оценки, соответствующие базисным векторам, то это говорит о единственности оптимального плана. Если же нулевая оценка соответствует вектору, не входящему в базис, то в общем случае это означает, что оптимальный план не единственный.

Если единичной подматрицы не обнаруживается, то либо придется перебирать все подсистемы m уравнений с m неизвестными в надежде обнаружить неотрицательные решения, либо прибегнуть к методу искусственного базиса.

Метод искусственного базиса заключается в том, что для получения единичной подматрицы коэффициентов мы вводим в исходную задачу неотрицательные так называемые искусственные переменные и включаем их в целевую функцию с коэффициентом +М для задачи минимизации и с коэффициентом -М для задачи максимизации, где М>0 - сколь угодно большое число. Полученная задача называется расширенной по отношению к исходной. Искусственные переменные образуют начальное базисное решение. Применив симплекс-метод, необходимо вывести из базиса все искусственные переменные. Если удается доказать (или показать), что искусственные переменные полностью вывести из базиса невозможно, то это означает, что задача не имеет решения, то есть ее ограничения противоречивы.

Если на текущей итерации из базиса выводится искусственная переменная, то в следующей симплекс-таблице соответствующий ей столбец можно удалить, в дальнейших итерациях он не будет участвовать.