20(1). Способы задания кривой на плоскости.

1. Параметризованная кривая. Пусть I: отрезок, интервал, полуинтервал, вся числовая ось, или объединение ин­тервалов и т.д.

Дифференцированная ф-ция f наз. гладкой, если ее первая произв. ф-ция непрерывна

Гладкое отображение множества I в пространство задается уравнениями:

, , (1)

где, - декартовы координаты на плоскости, a - гладкие функции. Отображение (1) наз. регулярным в точке t если в этой точке хотя бы одна из производных отличны от нуля.

Пусть хотя бы одна точка отображения (1) являет­ся регулярной (в противном случае образ состоит из одной точки). Тогда образ l отображения (1) вместе с самим этим отображени­ем называется параметризованной кривой. Переменная t наз-ся параметром, или криволинейной координатой на кривой l. С кинематической т.зр. уравнения (1) явл. ур-ями движения точки по траектории l. Положение точки на траектории в момент времени t определяется коорд-ми , . Поэтому параметр-ную кр. называют также путем.

2. Простая кривая. Применяя теорему о неявной функции, можно доказать, что у каждой регулярной точки плоской параметризованной кривой сущ. окрестность в I, образ которой при отображении (1) есть простая кривая, т.е. график гладкой функции

. (2)

теорема (о неявной ф-ции): пусть - регул-я точка параметр-ной кривой, заданной (1) . Тогда у точки сущ-ет -окрестность, такая, что образ этой окрестности при отображении , представляет собой простую кривую.

3. Общая кривая. Множество точек плоскости координаты которых связаны урав­нением

F(x,y) = 0, (3)

где F(x,y) - гладкая ф-ция, назовем общей кривой. Точка М общей кривой называется особой, если обе частные про­изводные функции F(x, у) в этой точке обращаются в нуль: .

Обычно предполагают, что общая кривая имеет хотя бы одну не­особую т. . Тогда по теореме о неявной ф-ции у этой точ­ки сущ-ет такая окрестность на плоскости Оху, внутри которой кривая (3) представляет собой график гладкой ф-ции (или ). Говорят, что ур-ие (3) неявно задает функцию . Т.о, общая кривая составлена из простых кривых, "склеен­ных" в особых точках.

Если общую кривую можно определить уравнением (3), левая часть которого представляет собой многочлен от перемен­ных х и у, то кр. называется алгебраической. Наименьшая степень многочлена, который определяет алгебр-кую кр., называет­ся порядком этой кривой. Если из ур-ний (1) исключить параметр t, то получим ур-е вида (3). Обратно, если в уравнении (3) положить х = x(t), где x(t) - произ­в. гладкая ф-ция, то из ур-я F(x(t),y)=0 можно выразить у = y(t). Если плоская кривая l задана как уравнением (3), так и параметризацией (2), то подстановка х = x(t), у = y(t) в ур-е (3) обращает последнее в тождество: F(x(t),y(t)) = 0.

Напр., общая кр. может быть задана как пара­метризованная кривая , , .

замечание. Указанные замены переменных могут не яв­ляться эквив-ми преобразованиями.

Напр., полагая в ур-нии гиперболы x=cht, получим параметр-кие ур-я , , , задающие лишь одну из ветвей гиперболы (т.к. х > 0). Лучше так: в делаем замену , тогда парам-кое ур-е гипеболы (уже обе ветви гиперболы будут описаны) будет иметь вид:

.

Парам. ур-е эллипса: .

Параметр. ур-е параболы ( )

.

Ур-я (1) параметр-ной кривой в векторной форме (4)

где - радиус-вектор т. M(t) кривой (1).

Прямая, проходящая через две различные т. и кривой l называется секущей.

Касательной к кривой l в точке наз-ся прямая, которая явл-ся предельным положением секущей при (если это предельное положение существует).

Т еорема. Пусть - регулярная точка параметризованной кри­вой, заданной ур-ем (4) ( ). Тогда вектор лежит на касательной к кривой в точке .

Док-во ,

.

При соответственно

тогда

,

т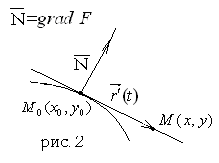 .е. предельное положение (направляющий вектор секущей) есть , а поскольку предельное положение секущей – касательная, то будет лежать на касательной в т. . Ч.т.д.

Ур-е касат. в т. , к параметр-ой кривой, имеет вид

где , , .

Пусть кривая задана общим уравнением F(x,y) = 0.

Теорема. вектор направлен перпендикулярно касательной, проведенной к кривой, в точке .

Док-во F(x,y) = 0, но , ,тогда F(x(t),y(t)) = 0. продиф-руем по t и найдем значение в точке :

, (5)

причем - координаты вектора ,

а корд. век. . тогда получается, что (5) – скалярное произведение ( , )=0, а это означает перпенд-сть. ч.т.д.

С помощью вышеупомянутых теорем можно записать следующие ур-я касательной и нормали. Ур-е касательной в точке , для общей кривой:

поскольку перпендик. .

Ур-е нормали в точке , для общей кривой:

.