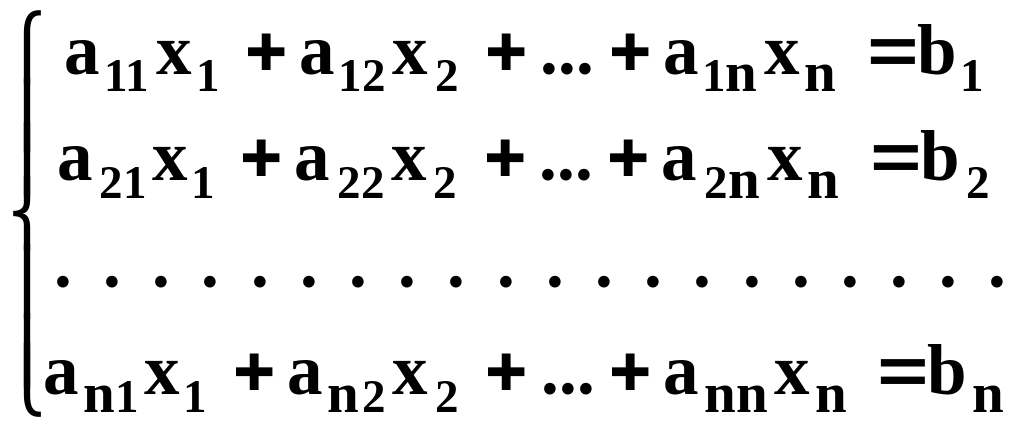2. Решение систем линейных алгебраических уравнений
Системы линейных алгебраических уравнений (СЛАУ) широко используются во многих областях прикладной математики. Оставляя за рамками данной работы вопросы теории линейных систем, отметим, что некоторые СЛАУ могут вообще не иметь решения или иметь бесконечное множество решений. В дальнейшем мы будем рассматривать только системы, имеющие единственное решение.
В общем виде система из n уравнений с n неизвестными выглядит так:
|
(2.1) |
Таким образом, даны квадратная матрица коэффициентов при неизвестных {aij}, i, j = 1, 2, … , n, и вектор-столбец свободных членов (правых частей уравнений) {bi }, i = 1, 2, … , n. В результате решения требуется определить n неизвестных x1, x2, … , xn, которые удовлетворяют одновременно всем уравнениям системы.
Все методы решения СЛАУ делятся на две группы – прямые и итерационные. Прямые методы дают решение после выполнения конечного числа операций. Эти методы достаточно универсальны, но в ряде случаев полученное решение не является достаточно точным. Итерационные методы используют последовательные приближения (итерации) к искомому результату. Они позволяют получить решение с любой заданной точностью, но при их использовании заранее неизвестно количество предстоящих итераций, более того, итерационные методы в некоторых случаях вообще не дают решения.
В данном пособии мы рассмотрим по одному методу из каждой группы.
Метод Гаусса
Суть метода состоит в следующем. Вначале квадратную матрицу коэффициентов при неизвестных преобразуют в верхне-треугольную матрицу (прямой ход). Для этого сначала первое неизвестное исключают из второго и последующих уравнений системы, затем второе неизвестное исключают из третьего и последующих уравнений и так далее. Таким образом, в последнем уравнении остается только одно неизвестное. Для реализации прямого хода используют следующие известные правила:
- любое уравнение системы можно умножить на постоянный коэффициент;
- можно сложить два любых уравнения системы и результат записать вместо одного из этих уравнений.
На втором этапе последовательно вычисляют значения всех неизвестных, начиная с последнего (обратный ход).
Рассмотрим применение метода Гаусса на примере. Пусть имеем такую систему из трех уравнений:
(2.2)
Для исключения первого неизвестного из второго уравнения умножим первое уравнение на (-a21/a11), т.е. на –0,5. Первое уравнение примет вид
-2x1 – 0,5x2 + 0,5x3 = -1,5.
Сложив его со вторым уравнением исходной системы (2.2), получим
– 2,5x2 + 1,5x3 = -0,5.
Можно заметить, что неизвестное x1 в данном уравнении отсутствует.
Для исключения первого неизвестного из третьего уравнения системы (2.2) умножим первое уравнение этой системы на (-a31/a11), т.е. на –0,25. Первое уравнение примет вид
-x1 – 0,25x2 + 0,25x3 = -0,75.
Сложив его с третьим уравнением исходной системы (2.2), получим
-1,25x2 + 2,25x3 = 4,25.
Можно заметить, что и в этом уравнении неизвестное x1 отсутствует.
Таким образом, система (2.2) примет вид
4
x1
+ x2
– x3
= 3
-2,5x2 + 1,5x3 = -0,5 (2.3)
-1,25x2 + 2,25x3 = 4,25
Теперь исключим неизвестное x2 из третьего уравнения системы (2.3), сложив его со вторым уравнением системы (2.3), умноженным на –0,5. Получим систему
4
x1
+ x2
– x3
= 3
-2,5x2 + 1,5x3 = -0,5 (2.4)
1,5x3 = 4,5
Прямой ход закончен, исходная матрица коэффициентов приведена к верхне-треугольному виду. В третьем уравнении системы (2.4) присутствует только неизвестное x3. Теперь легко осуществить обратный ход, т.е. вычислить неизвестные. Из третьего уравнения вычислим x3, далее его значение подставим во второе уравнение и вычислим x2, а затем из первого уравнения найдём x1. Получим ответ: x1 = 1; x2 = 2; x3 = 3. Задача решена.
Программа для решения СЛАУ методом Гаусса может иметь такой вид:
program SLAU1; {Решение системы линейных уравнений методом Гаусса}
uses crt;
const n=3;
var a:array [1..n,1..n] of real;
b,x: array [1..n] of real;
i,j,k: integer; c,s: real;
begin
{Ввод исходных данных}
for i:=1 to n do
begin
writeln (‘Введите коэффициенты уравнения’,i);
for j:=1 to n do read (a[i,j]);
writeln (‘Введите свободный член уравнения’,i);
readln (b[i]);
end;
{Прямой ход}
for k:=1 to n-1 do
begin
for i:=k+1 to n do
begin
c:=-a[i,k]/a[k,k]; a[i,k]:=0;
for j:= k+1 to n do a[i,j]:=a[i,j]+c*a[k,j];
b[i]:=b[i]+c*b[k];
end;
end;
{Oбратный ход}
x[n]:=b[n]/a[n,n];
for i:=n-1 downto 1 do
begin
s:=0;
for j:=i+1 to n do s:= s+a[i,j]*x[j];
x[i]:=(b[i]-s)/a[i,i];
end;
{Вывод результатов}
writeln (‘Решение системы’);
for i:=1 to n do write (x[i]:8:4);
writeln;
end.