9. Построение разностной схемы. Оду 2-го порядка.

Рассмотрим ДУ

С краевыми условиями -краевая задача 1 рода

-краевая задача 2 рода

-краевая задача 3 рода

Эти краевые задачи имеют единственное решение, когда . Тогда . При таких условиях краевая задача корректно поставлена. Построим дискретную модель:

В зависимости от требований точности, от порядка точности метода, от условия устойчивости, выбираем .

1. -число разбиений. -число точек сеточного аргумента(т.е.длины массивов для сеточных функций в этой задаче) -число внутренних точек, в которой ищется решение. В результате построим равномерную сетку аргумента.

2.Ддля простоты точно заданы .

3.Линейный дифференциальный оператор заменяем разностным. Для получения разностных отношений в виде дискретных представим решение в виде 2-ух разложений по формуле Тейлора:

Из такого разложения получаем:

В итоге получим разностный оператор в виде:

4.Разностная схема это совокупность конечно разностных уравнений и условий.

Приведем эту разностную схему к удобному виду для исследования устойчивости.

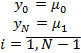
Пример.

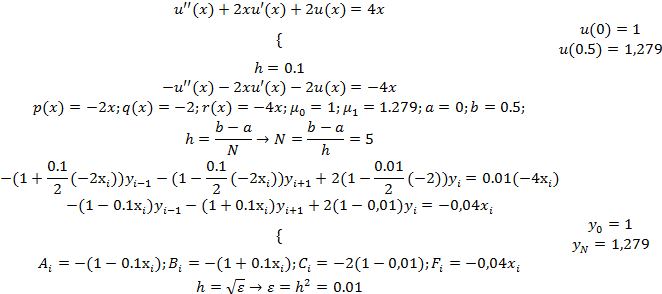
Где -погрешность.

Билет 11.

Дана линейная краевая задача первого рода. Привести определение сходимости трех точечной разностной схемы приближенного решения этой задачи . Доказать теорему сходимости.

Рассмотрим ДУ:

Краевые условия первого рода:

Запишем разностное уравнение для погрешности точное решение разностной схемы,

– уравнение для погрешности

при точном задании краевых условий на границе:

Теорема: Если разностная схема устойчива и аппроксимирует исходную задачу с порядком О(h²), то существует . Т.е. разностная схема сходится с порядком h².

Замечание: Если задана погрешность ε, то по ней и по тому что h≤2/p^*, можно выбрать шаг h=(b-a)/N. То. чтобы h .

Алгоритм:

-выбрать N и h

-задать p,q,r

-построить коэффициенты A_i,B_i,C_i,F_i

-осуществить прогонку:

прямой ход: α₁=0, β₁=μ₀, i=1,…N

,

обратный ход: y[N]=μ₁, i=N-1,..0

Пример.

Построить разностную схему второго порядка точности для краевой задачи

//Заебись пример. E4

13. Провести построение разностной схемы методом баланса для линейной краевой задачи с краевыми условиями первого рода с оду.

Интегро-интерполяционный метод (метод баланса)

Простейшая задача : стержень без поперечного сечения, но с массой. Распространение тепла идет вдоль стержня в момент времени. Возникает тепловой поток

k(x)- коэффициент теплопроводности,

u- температура

q(x)- коэффициент теплообмена с окружающей средой

, - плотность источников тепла.

Проинтегрируем на

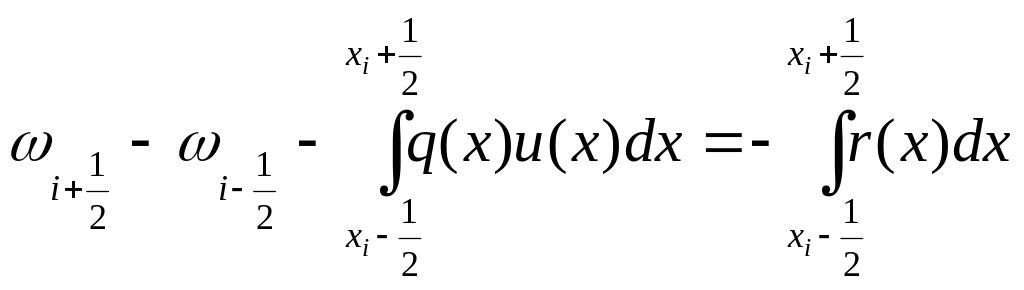- уравнение теплового баланса.

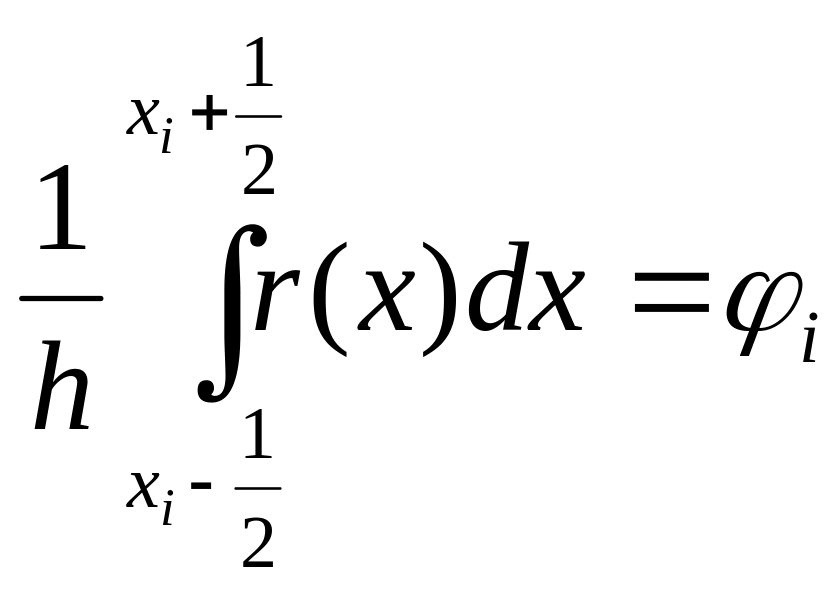- средняя величина

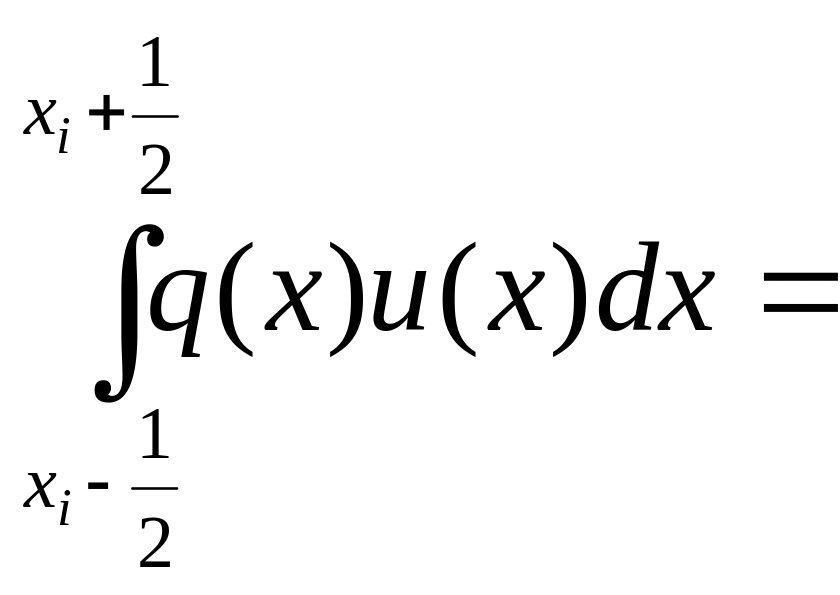заменим u(x) интерполяционным многочленом 0-ой степени, т.е константой

Для потока рассмотрим формулу : . Проинтегрируем эти выражения

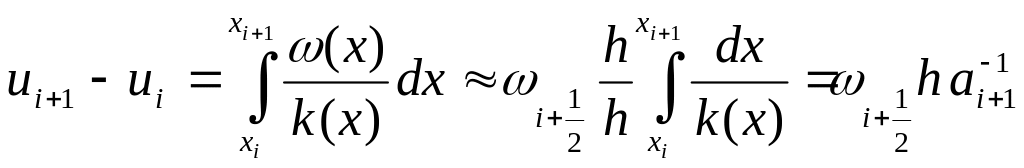, где

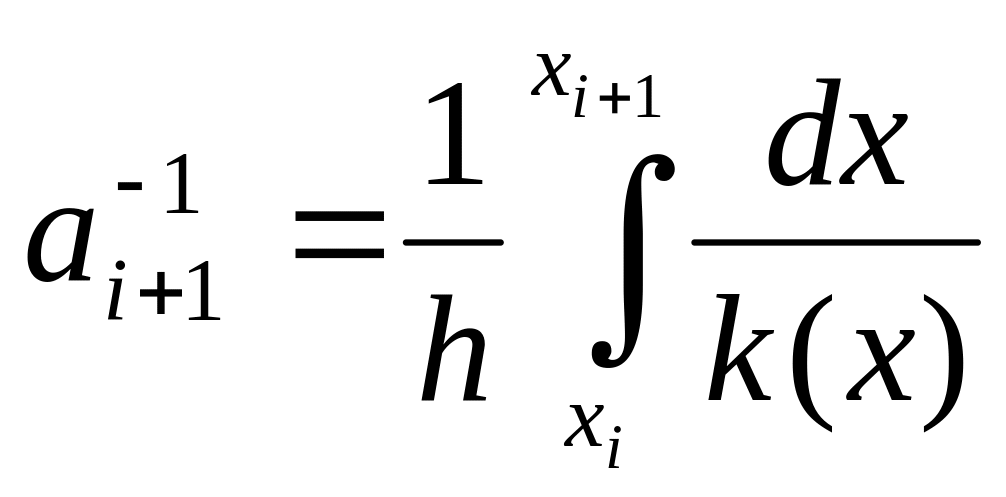
В итоге , где ,

Для решения этой разностной схемы используется метод прогонки с коэффициентами

1. метод неопределенных коэффициентов

2. конечно-разностный метод

3. метод баланса

14. Пример. Методом баланса построить консервативную разностную схему с h=0.1 для краевой задачи

.

Решение:

, (в обозначениях из теории)

15.

Привести постановку линейной и нелинейной краевой задачи для ОДУ 2 порядка. Провести построение метода сведение к решению задачи Коши (метод пристрелки).

Дана линейная краевая задача:

(6)

Могут быть также кр. Усл. 1-го и 2-го рода:1) ; , но случай с усл. 3-го рода – общий.

Для применения метода пристрелки, сделаем замену переменных:

В результате получим систему вида:

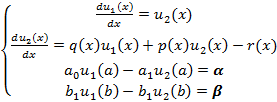(7)

Общее решение системы ОДУ в (7) представим.

(x)

(2)

Для применения метода Руне-Кутты, соответствующие задачи Кошипредставим в виде задач для системы ОДУ первого порядка:

Неоднородной:

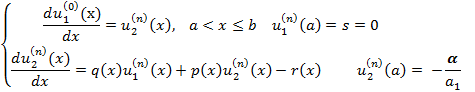
Для однородной задачи r(x)=α= получим:

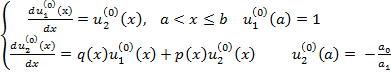(9)

Чтобы (2)было решением (6) выберем с из краевого условия для точки x=b в (6). По найденному получим

(10)

Решение исходной краевой задачи находим, подставляя

Пример: решить методом пристрелки: y’’+98.1siny=0, y’(0)=0, y (1)= .

Делаем замену . Краевые условия запишем в виде:

. Тогда нам нужно решить две задачи Коши:

неоднородная задача:

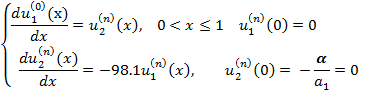
однородная:

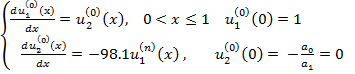
Замечание: уравнения однородны и в первом и во втором случаях, разл. только нач. усл.

Решение будем произв, например, методом Р.-К. 4-го порядка точности:

Представив системы в векторном виде применяем формулы метода Р.-К.

,

После тог, как алгоритм Р.-К. отработал мы получим . Тогда . И, наконец,