
- •Оглавление
- •Численное решение итерационным методом
- •2D уравнения теплопроводности
- •Разработка фрагмента исходного кода для численного решения итерационным методом 2d уравнения теплопроводности
- •Интерфейс графических устройств gdi
- •Фрагмент функции void Child_Rgn_Zg_OnPaint(hwnd hwnd…)
- •Входящие программы
- •Список литературы
Оглавление
Численное решение итерационным методом 2
2D уравнения теплопроводности 2
Разработка фрагмента исходного кода для численного решения итерационным методом 2D уравнения теплопроводности 4
Интерфейс графических устройств GDI 6
Фрагмент функции void Child_Rgn_Zg_OnPaint(HWND hwnd…) 14
Входящие программы 21
Список литературы 23
Численное решение итерационным методом
2D уравнения теплопроводности
Уравнение теплопроводности – нестационарное (изменяющееся со временем) дифференциальное уравнение в частных производных, для 2D случая имеет следующий вид:
 ,
(1)
,
(1)
где
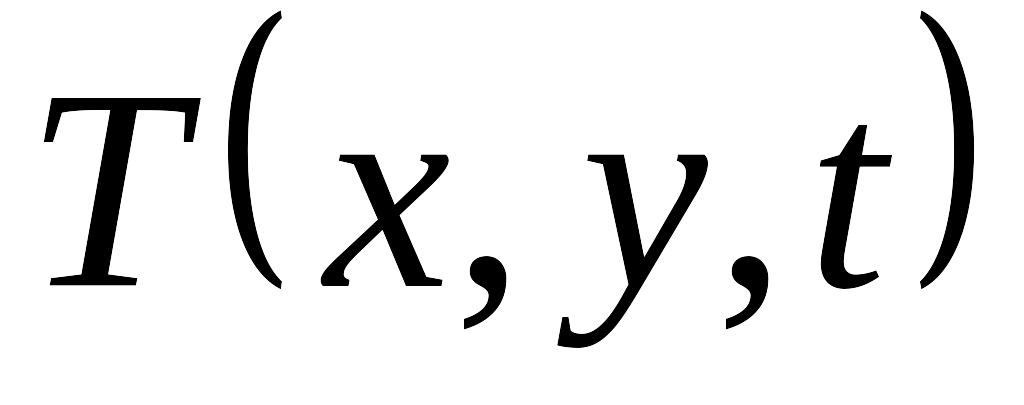 – нестационарное
2D
распределение
температуры,
– нестационарное
2D
распределение
температуры,
 – коэффициент
теплопроводности материала.
– коэффициент
теплопроводности материала.
Введём
в функциональном 3D
пространстве
![]() сетку с шагами
сетку с шагами
![]() .
Для удобства вычислений – равномерную
по пространственным переменным
.
Для удобства вычислений – равномерную
по пространственным переменным
![]() :
:
![]() .
В основе простейшего итерационного
конечно-разностного метода решения
дифференциальных уравнений в частных
производных лежит замена:
.
В основе простейшего итерационного
конечно-разностного метода решения
дифференциальных уравнений в частных
производных лежит замена:
в правой части (1) вторых производных центральными разностями по
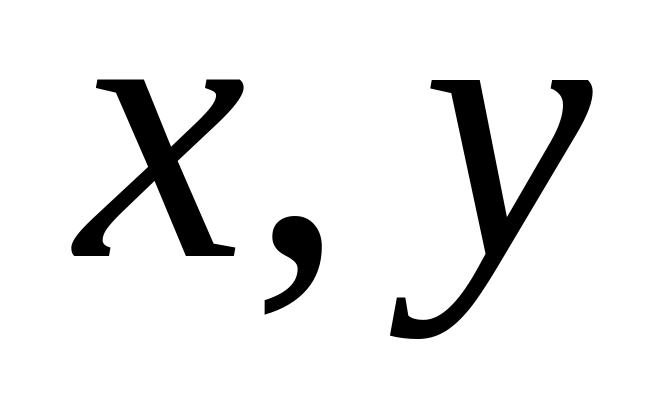 ;
;
в левой части (1) первой производной разностью вперёд по
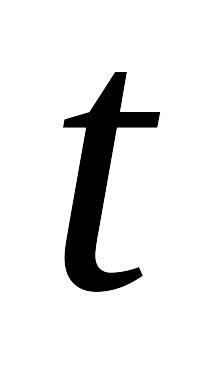 .
.
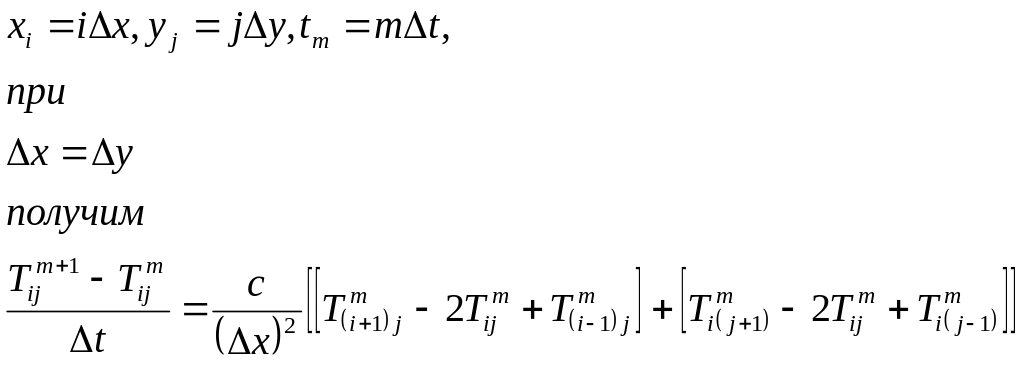 .
(2)
.
(2)
Конечно-разностное уравнение (2) преобразуем в форму, удобную для итерационного решения:
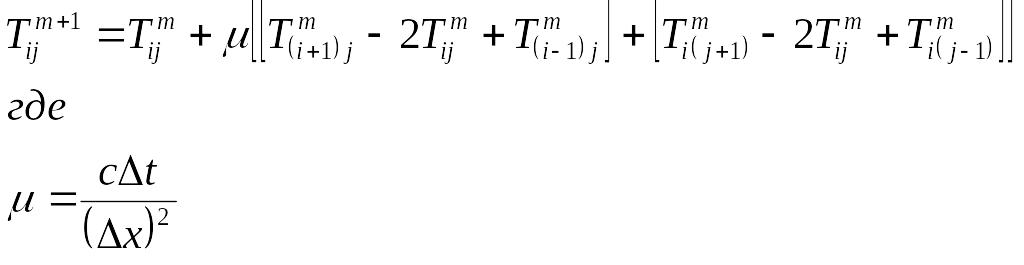 .
(3)
.
(3)
Форма
(3) записи уравнения теплопроводности
(1) и (2) позволяет находить следующее по
времени
![]() значение
значение
![]() исходя из известных на данный момент
исходя из известных на данный момент
![]() текущих значений
текущих значений
![]() .
Для итерационного процесса необходимо
задать начальные и граничные условия.
.
Для итерационного процесса необходимо
задать начальные и граничные условия.
Начальные
условия определяют начальное 2D
распределение значений
![]() при
при
![]() .
Например, в начальный момент времени
точка с координатами
.
Например, в начальный момент времени
точка с координатами
![]() разогрета некоторым внешним воздействием
(удар микрометеорита по корпусу КА,
точечная подсветка мощным импульсом
лазерного излучения, монтажник точечно
задел горячим паяльником и т.п.) до
некоторой температуры:
разогрета некоторым внешним воздействием
(удар микрометеорита по корпусу КА,
точечная подсветка мощным импульсом
лазерного излучения, монтажник точечно
задел горячим паяльником и т.п.) до
некоторой температуры:
![]() .
(4)
.
(4)
Граничные условия определяют ситуацию на границах 2D диапазона вычислений
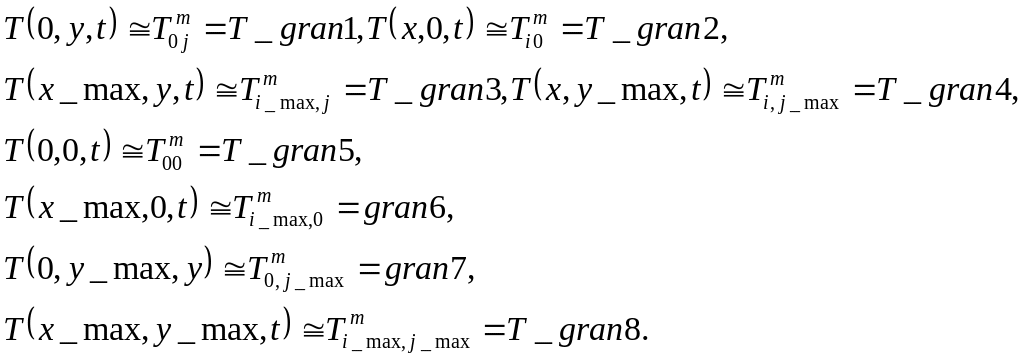 (5)
(5)
Пусть внешнее воздействие в заданной точке привело к разогреву до температуры:
![]() ,
,
а температура на границах диапазона вычислений равна температуре окружающей среды, для простоты – комнатной температуре:
![]() .
.
Имея
форму итерационной записи (3), начальные
(4) и граничные условия (5), можно найти
решение уравнения (1), то есть, рассчитать
динамику изменения 2D
распределения температуры
![]() для последовательных моментов времени
для последовательных моментов времени
![]() .
.
Значение
коэффициента теплопроводности
является
табличной величиной и берётся из
физических справочников. Имеет размерность
![]() .
Вообще-то, коэффициент теплопроводности
является функцией температуры:
.
Вообще-то, коэффициент теплопроводности
является функцией температуры:
![]() ,
но для упрощения расчётов примем, что
коэффициент теплопроводности является
константой и будем использовать табличные
значения при T=300K:
,
но для упрощения расчётов примем, что
коэффициент теплопроводности является
константой и будем использовать табличные
значения при T=300K:
![]() .
.
№ |
Материал (T=300K) |
Теплопроводность, Вт/см·К |
1. |
SiO2 (аморфный) |
0,014 |
2. |
Ge |
0,6 |
3. |
Si |
1,5 |
4. |
GaAs |
0,46 |
