2.Выбор электродвигателя и кинематический расчет

2.1 Выбор электродвигателя

По табл. 1.1 примем: КПД пары конических зубчатых колёс η₁ =0,97,

коэффициент, учитывающий потери пары подшипников качения η₂=0,99, КПД открытой цепной передачи η₃=0,96, коэффициент.

Общий КПД привода:

η=η₁² ·η₂·η3=0,99²·0,99·0,96 =0,904

Требуемая мощность электродвигателя:

P_тр = 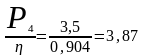кВт

С учётом требуемой мощности Р_тр = 3,87 кВт рассмотрим возможность выбора асинхронных двигателей серии 4А с номинальной мощностью Р_н = 4 кВт.

Номинальная частота вращения n_н = 719 (об/мин);

Передаточное отношение клиноременной и зубчатой передачи iкл= 3,425, i_кон=3, тогда общее передаточное отношение привода

iобщ=3,425·3=10,275

Выбираем трёхфазный асинхронный электродвигатель типа 4A132S8 УЗ со следующими параметрами;

• номинальная мощность Р_н = 4 кВт;

• номинальная частота вращения n_ном = 719 об/мин;

- отношение пускового момента к нормальному Тп/Тн=1,8.

2.2 Передаточные отношения привода и отдельных его передач

Общее передаточное отношение привода при частоте вращения его входного вала n₁=n_н

i_общ= n₁/n₄= n_н/n₄ = 719/70 = 10,27

Примем /2, с.6/ передаточные отношения – для зубчатой и цепной передач редуктора соответственно i_кон = 3, iкл = 3,425.

2.3 Частоты вращения, угловые скорости, мощности и моменты на валах привода

Частоты вращения валов:

n₁ = n_н = 719 (об/мин);

n₂ = n₁ = 719 (об/мин);

n₃ =n₂/i_кон = 719/3,425 = 210 (об/мин);

n₄ = n₃/i_ц =210/3 = 70 (об/мин).

Угловые скорости валов:

ω₁ = π·n₁/30 = 3,14·719/30 = 75,28 (рад/с);

ω₂ = ω₁ = 75,28 (рад/с);

ω₃ = ω₂/i_кон = 75,28/3,425 = 21,9 (рад/с);

ω₄ = ω₃/iц = 21,9/3 = 7,3 (рад/с).

Мощности на валах:

P₁ = P_тр = 3,87 (кВт);

Р₂ = Р₁ = 3,87 (кВт);

Р₃ = Р₂·η_кл·η_подш = 3,87·0,96·0,99 = 3,72 (кВт);

Р₄ = Р₃·η_кон·η_подш = 3,72·0,97·0,99 = 3,6 (кВт).

Моменты на валах:

Т₁ = P₁/ ω₁ = 3,87*10³/75,28 = 51,4 (Н*м);

Т₂ = P₂/ ω₂ = 3,87*10³/75,28 = 51,4 (Н*м);

Т₃ = P₃/ ω₃ = 3,72*10³/21,9 = 169,8 (Н*м);

Т₄ = P₄/ ω₄ = 3,6*10³/7,3 = 493,2 (Н*м).

Максимальные моменты на валах:

Т_1max = Т₁· Тп/Тн = 51,4·1,8 = 92,52 (Н*м);

Т_2max = Т₂· Тп/Тн =51,4·1,8 = 92,52 (Н*м);

Т_3max = Т₃· Тп/Тн = 169,8·1,8 = 305,64 (Н*м);

Т_4max = Т₄· Тп/Тн = 493,2·1,8 = 887,76 (Н*м).

№ вала по рис. 1	n, об/мин	ω, рад/с	Р, кВт	Т, Н*м	Тmax, Н*м
1	719	75,28	3,87	51,4	92,52
2	719	75,28	3,87	51,4	92,52
3	210	21,9	3,72	169,8	305,64
4	70	7,3	3,6	493,2	887,76

Таблица 2.3 - Частоты вращения, угловые скорости, мощности и моменты на валах привода.

3. Расчёт зубчатых колёс редуктора

По табл. 3.3 принимаем для шестерни сталь 45, твердости HB 230; для колеса сталь 45, твердости HB 200.

Допускаемое контактное напряжение:

[δ_H]= .

δ_{Hlim b} –предел контактной выносливости при базовом числе циклов.

По табл. 3.2 для углеродистых сталей с твёрдостью поверхности зубьев менее HB 350 и термообработкой улучшением для колеса δ_{Hlim b} =2HB+70=530.

К_HL – коэффициент долговечности, при длительной эксплуатации К_HL=1.

[n]_H – коэффициент безопасности, при улучшении [n]_H=(1,1÷1,2), принимаем [n]_H=1,15

Находим допускаемое напряжение по колесу:

[δ_H]= 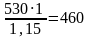МПа

Коэффициент нагрузки при консольном расположении шестерни по табл. 3.1 принимаем К_HB=1,3.

Коэффициент ширины венца по отношению к внешнему конусному расстоянию Ψ_ВRe=0,285.

Внешний делительный диаметр колеса

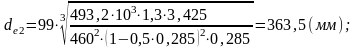
принимаем по стандарту СТ СЭВ 229-75 ближайшее значение d_е2=355 мм.

Примем число зубьев шестерни Z₁=20, число зубьев колеса Z₂=Z₁·u=20·3,425=68,5.

Примем z₂=69, тогда u = z₂ /z1 = 69/20=3,45.

Отклонение от заданного состовляет 0,72%, что меньше установленных ГОСТ 12289-76 3%.

Внешний окружной модуль

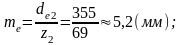
Углы делительных конусов :

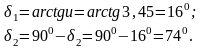
Внешнее конусное расстояние 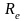и длина зуба

принимаем =54мм.

Внешний делительный диаметр шестерни:

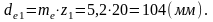
средний делительный диаметр шестерни:

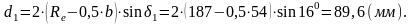
внешние диаметры шестерни и колеса (по вершинам зубьев):

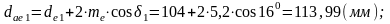
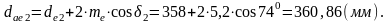
Средний окружной модуль

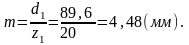
Средняя окружная скорость колес

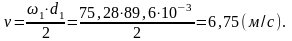
Для конической передачи назначаю 7-ю степень точности.

Для проверки контактных напряжений определяем коэффициент нагрузки:

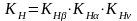
при 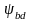=0,6 , консольном расположении колес и твердости HB<350 коэффициент, учитывающий распределение нагрузки по длине зуба, 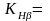1,24 /1, стр.39/.

Коэффициент, учитывающий распределение нагрузки между прямыми зубьями, 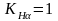/1, стр.39/.

Коэффициент, учитывающий динамическую нагрузку в зацеплении, для прямозубых колес при 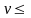5 м/с 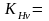1,05 /1, с.40/.

Таким образом, 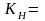1,24∙1∙1,05=1,3.

Проверяем контактное напряжение по формуле

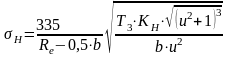
Силы в зацеплении:

Окружная

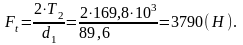
Радиальная для шестерни, равная осевой для колеса

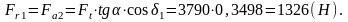
Осевая для шестерни, равная радиальной для колеса

Проверка зубьев на выносливость по напряжениям изгиба:

.

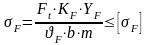Коэффициент нагрузки

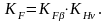
при 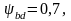консольном расположении колес, валах на роликовых подшипниках и твердости НВ<350 значениях 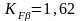/1, стр.43/.

при твердости НВ<350, скорости v=6,75 м/с и 7-й степени точности 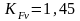/1, с.43/.

Итак,

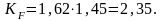
Y_F-коэффициент формы зуба выбираем в зависимости от эквивалентных чисел зубьев:

для шестерни

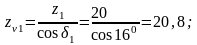
для колеса

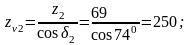
При этом Y_F1 = 4,1 и Y_F2 = 3,61 /1, стр.42/.

Допускаемое напряжение при проверке зубьев на выносливость по напряжениям изгиба

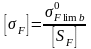
для стали 40Х улучшенной при твердости НВ<350 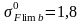НВ /1, с.44/.

Для шестерни

для колеса

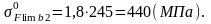
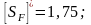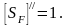коэффициент запаса прочности . По /1, стр.44/ для поковок и штамповок таким образом,

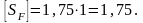
Допускаемое напряжение при расчете зубьев на выносливость:

для шестерни

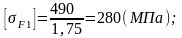
для колеса

для шестерни отношение

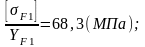
для колеса

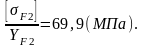
Дальнейший расчет ведём для зубьев шестерни, так как полученное отношение для него меньше.

Проверяем зуб шестерни: