Задачи на построение графа.

1. Построить ациклический связный граф на 13 вершинах, если известно, что 2 вершины имеют степень 4, 1 вершина степени 3, 1 вершина степени 2 и 8 вершин степени 1 или обосновать невозможность построения.

2. Построить граф на 12 вершинах. Известно, что граф содержит 2 цикла и имеет 5 вершин степени 3, 1 вершину степени 2 и 5 вершин степени 1.

3. Построить связный двудольный граф на 12 вершинах. Известно, что в графе имеются 2 вершины степени 4, 4 вершины степени 3 и 2 вершины первой степени.

Задачи на вычисление цикломатического и хроматического чисел.

1. Определить все возможные значения хроматического числа для связных графов на 72 вершинах, цикломатическое число которых не превосходит 2.

2. Определить все возможные значения хроматического числа для графа 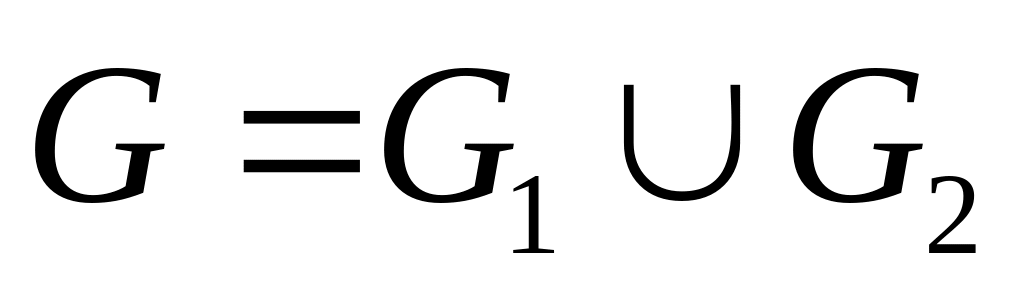, где G₁ и G₂ – простые циклы длины 4.

3. Вычислить цикломатическое и хроматическое числа графа 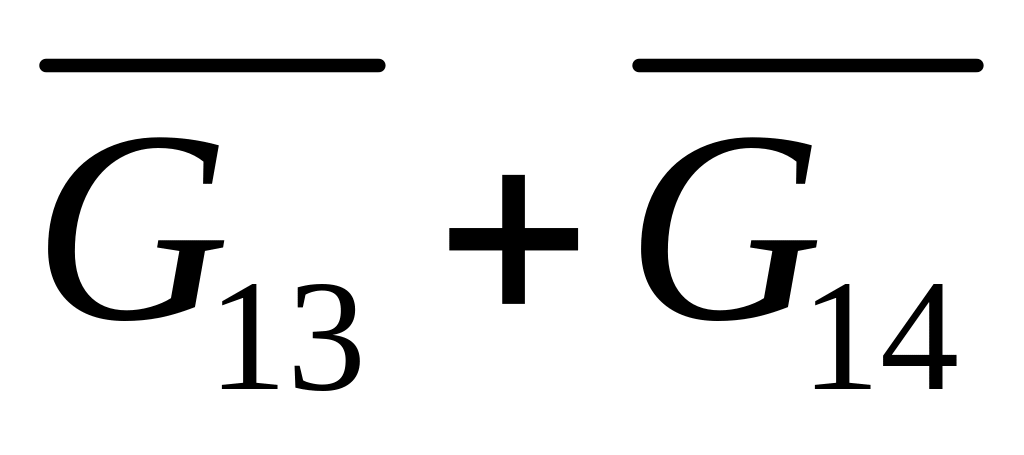, где G₁₃ и G₁₄ – полные графы на 13 и 14 вершинах соответственно, в каждом из которых удалено по 5 рёбер, образующих простой цикл. Носители графов не имеют общих вершин.

4. Вычислить цикломатическое и хроматическое числа графа , где G₅ и G₂₆ – графы, являющиеся простыми циклами на 5 и 26 вершинах соответственно. При этом носители графов имеют две общие вершины.

5. Вычислить цикломатическое и хроматическое числа графа , где K_16,7 – полный двудольный граф, у которого удалено одно ребро, G₁₅ – простой цикл на 15 вершинах. Оба графа имеют 1 общую вершину.

6. Вычислить цикломатическое и хроматическое числа графа , где 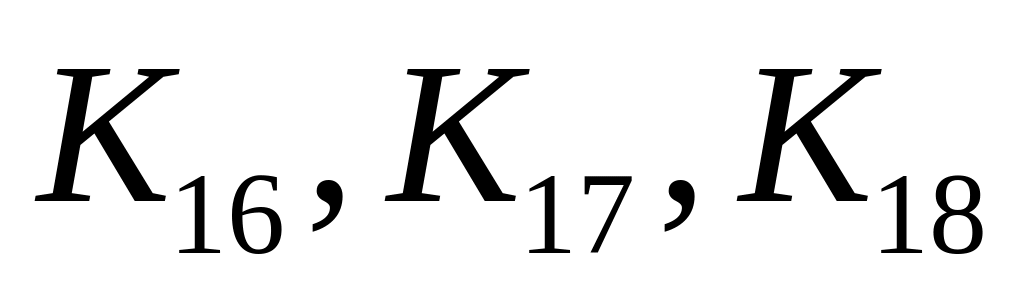- полные графы на 16, 17 и 18 вершинах, у каждого удалено по 2 смежных ребра, носители не имеют общих вершин.

Задачи на рёберность графов, внутреннюю, внешнюю устойчивость, планарность и раскраску.

1. Вычислить число внешней устойчивости графа 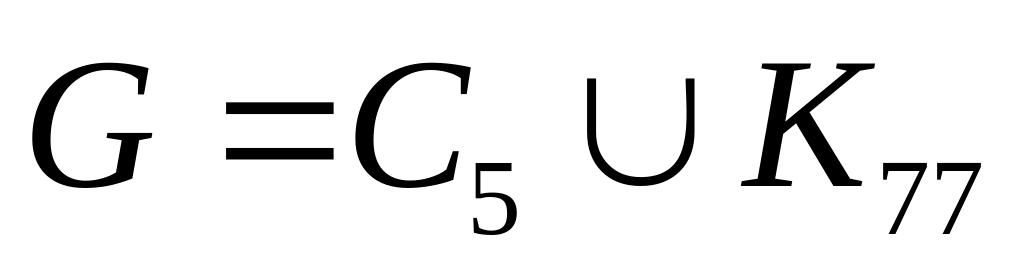, где - простой цикл на 5 вершинах, - полный граф на 77 вершинах. Графы имеют 1 общую вершину.

2. Для заданного графа указать все пустые подграфы, определить число внутренней и внешней устойчивости, раскрасить граф, выяснить, является ли граф планарным, если да – то уложить на плоскости.