42 Использование обратных связей для повышения качества.

Обратные связи могут быть положительными и отрицательными. Кроме того, обратные связи могут быть жесткими и гибкими. Рассмотрим передаточную функцию, записанную для случая отрицательной обратной связи. Из этого выражения найдем передаточную функцию для установившегося режима, для чего необходимо положить : .

Здесь может быть два случая. Если выполняется условие , что будет при использовании в цепи обратной связи дифференцирующих элементов, то в установившемся режиме . Это означает, что в этом режиме передаточная функция цепи, охваченной обратной связью, будет равна передаточной функции исходной цепи. Такая обратная связь называется гибкой. Нетрудно видеть, что гибкая обратная связь действует только в переходных режимах, а в установившемся режиме она как бы отклю­чается.

Если , то обратная связь действует не только в переходном, но и в установившемся режиме. В этом случае обратная связь называется жесткой.

Заметим, что случай, когда звено, охватываемое обратной связью, отно­сится к числу интегрирующих звеньев и не вносит особенностей. Здесь по-прежнему условие будет соответствовать случаю гибкой обратной связи, так как числитель будет стремиться к бес­конечности быстрее, чем знаменатель, и результирующая передаточная функция так же, как и передаточная функция исходной цепи. Заметим также, что понятие гибкой или жесткой обратной связи связано с той величиной, которая принимается в качестве выходной в исходном звене.

В динамическом отношении отрицательные обратные связи могут оказы­вать самое различное действие. Однако подобно тому, как это было сделано для последовательных корректирующих устройств, можно наметить три основных вида отрицательных обратных связей:

1) обратные связи, подавляющие высокие частоты (аналоги пассивного последовательного интегрирующего звена);

2) обратные связи, подавляющие низкие частоты (аналоги пассивного последовательного дифференцирующего звена).

3) обратные связи, подавляющие средние частоты (аналоги пассивного последовательного интегро-дифференцирующего звена);

Установить аналогию обратной связи с тем или иным последовательным корректирующим звеном можно при помощи формул перехода (10.5) и (10.6). Особенно важно иметь возможность перехода от последовательного корректи­рующего звена к эквивалентной обратной связи. Это определяется тем, что расчетным путем наиболее просто определить параметры последовательного корректирующего звена, а с точки зрения технического осуществления наиболее удобны обратные связи.

43 Понятие желаемой лачх, методика ее построения.

П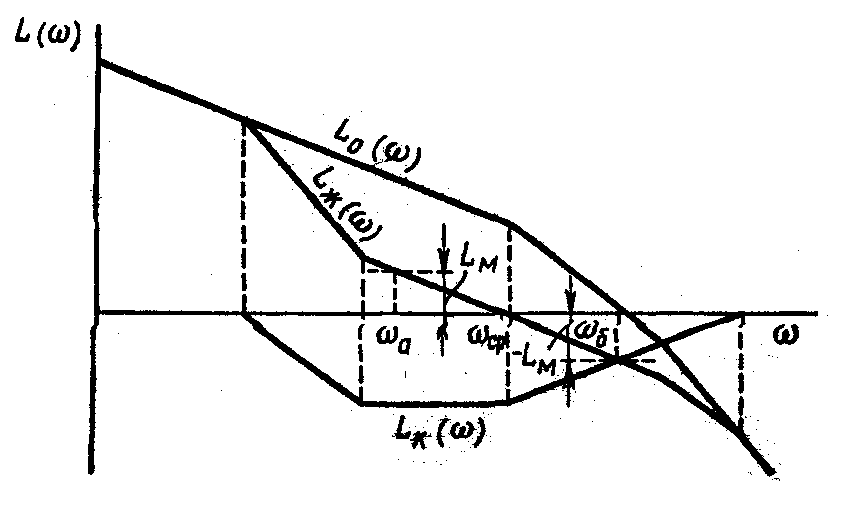 остроение желаемой ЛАЧХ. Желаемой называют асим­птотическую ЛАЧХ L_ж (w) разомкнутой системы, имеющей желаемые (требуемые) статические и динамические свойства. Желаемая ЛАЧХ состоит из трех основных асимп­тот: низкочастотной, среднечастотной и высокочастотной. Кроме того, могут быть сопрягающие асимптоты, которые со­единяют основные.

Строится желаемая ЛАЧХ на основании требований к си­стеме. Ранее было выяснено, что низкочастотная асимптота ЛАЧХ разомкнутой системы определяет статические cвойства. Если передаточная функция (5.37) разомкнутой системы имеет передаточный коэффициент k и порядок астатизма v, удовлетворяющие требованиям, то низкочастотной асимптотой желаемой ЛАЧХ L_ж (w) является низкочастотная асимп­тота ЛАЧХ L₀ (w) неизменяемой части системы. На рис. 5.23 показан именно такой случаи.

Среднечастотная асимптота ЛАЧХ разомкнутой системы и ее сопряжение с низкочастотной определяют динамические свойства системы — устойчивость и показатели качества переходной характеристики.

Построение среднечастотной асимптоты желаемой ЛАЧХ начинают с выбора частоты среза w_ср. Для этого использует­ся номограмма (рис. 5.24), составленная В. В. Солодовниковым. Она определяет зависимость перерегулирования от времени регулирования t_p от максимума Р_тах вещественной ча­стотной характеристики замкнутой системы, причем время регулирования t_р дано в виде функции частоты среза w_ср.

Номограмма используется следующим образом. По задан­ному значению перерегулирования о определяют значение Р_mаx. Затем по Р_mаx определяют соотношение между t_p и w_ср, т. е.

(5.38)

На рис. 5.24 показано, как по значению = 30% опреде­лено Р_mах = 1,27 и затем t_р = 3,5Пи/w_ср.

Из (5.38) вычисляют частоту среза w_ср1, при которой вре­мя регулирования не превысит заданного значения. Если при начальном рассогласовании g₀ ускорение регулируемой координаты ограничивается значением w, то частота среза не должна быть больше w_ср2, т. е.

(5.39)

Частота среза w_ср2 соответствует оптимальному переходному процессу при допустимом ускорении w.

Таким образом, частота среза должна быть выбрана по одному из следующих условий:

(5.40)

Чем больше w_ср, тем меньше время регулирования. Однако если w_ср2 < w_ср1, то w_ср не должна быть больше w_ср2. В этом случае требование в отношении времени регулирова­ния, возможно, не будет удовлетворено.

Среднечастотная асимптота желаемой ЛАЧХ проводится через точку w_ср наклоном —20 дБ/дек. При большем наклоне трудно обеспечить необхо­димый запас устойчивости и допустимое перерегули­рование.

Протяженность среднечастотной асимптоты уста­навливается исходя из не­обходимого запаса устой­чивости. Из этих же сооб­ражений выбирают ее со­пряжение с низкочастотной асимптотой. Кроме того, сопрягающую асимптоту следует выбирать так, что­бы характеристика L_ж (w) возможно меньше отлича­лась от L₀ (w) и корректирующее устройство было возможно бо­лее простым.

Д ля указанного выбора по ранее най­денному значению P_max с помощью кривых, показанных на рис. 5.25, определяют избыток фазы у и предельные значения L_M логарифмических амплитуд. Избыток фазы v должен быть обеспечен на том уча­стке характеристики Lж (w), для которого справедливо

Этот участок охватывает среднечастотную асимптоту и, возмож­но, часть сопрягающей асимптоты.

Сначала нужно провести прямую с ординатой L_M (пунктир на рис. 5.23). Затем нанести сопрягающую асимптоту. Если наклон низкочастотной асимптоты 0 или —20 дБ/дек, то на­клон сопрягающей асимптоты выбирается равным —40 или —60 дБ/дек. Начинать ее можно из точки среднечастотной асимптоты с ординатой L_M. После этого проверяют избыток фазы у_а при частоте w_а, где ордината L_ж (w) равна L_M. Зна­чение у_а подсчитывается по формуле

(5.42)

где v — порядок астатизма; w_i — сопрягающие частоту мень­ше w_а, при которых наклон L_ж (w) увеличивается на 20 дБ/дек; k — число сопрягающих частот w_i; w_j — сопрягающие частоты, меньшие w_a, при которых наклон L_m (w) уменьша­ется на 20 дБ/дек; I — число сопрягающих частот w_j.

Если фаза фи определяется каким-либо другим способом, то избыток фазы определяют как (5.43) где фи < 0.

Если избыток фазы у_а оказывается меньше необходимого, то сопрягающую асимптоту следует переместить влево. В про­тивном случае (при слишком большом избытке фазы) сопря­гающая асимптота перемещается вправо. Чем больший диапа­зон частот занимает низкочастотная асимптота, тем лучше система воспроизводит низкочастотные изменения задающего воздействия.

Высокочастотная асимптота желаемой ЛАЧХ мало влияет на свойства системы, поэтому ее следует выбирать так, чтобы корректирующее устройство было возможно более простым. Это достигается при совмещении высокочастотных асимптот характеристик L_ж (со) и L₀ (w). Если совмещение не удается, то высокочастотная асимптота L_ж(w) должна иметь тот же на­клон, что и высокочастотная асимптота L₀(w).

После выбора высокочастотной асимптоты желаемой ЛАЧХ и сопряжения ее со среднечастотной асимптотой проверяют избыток фазы у_б при частоте w_б, где ордината характеристики L_ж(w) равна — L_м т. е. (5.44)

где q_ср — относительный наклон среднечастотной асимпто­ты (при наклоне —20 дБ/дек q_ср = 1); w — сопрягающие ча­стоты, большие частоты среза w_ср; т — число частот w_y Если y_б меньше требуемого значения, то высокочастотную асимптоту желаемой ЛАЧХ нужно переместить вправо.