37 Статические и динамические ошибки.

В любой реальной CАУ невозможно точное равенство задающего воздействия g и управляемой величины y. Ошибку САУ при этом вычислим согласно уравнению ошибки как разность этих воздействий, т.е.:

Учитывая историю переходных процессов, ошибку можно представить в виде двух составляющих: установившейся (статической) и переходной (динамической):

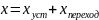
В линейных САУ установившаяся (статическая) ошибка определяется частным решением её дифференциального уравнения, а переходная (динамическая) ошибка – решением однородного дифференциального уравнения.

Таким образом, установившуюся ошибку САУ в неподвижном состоянии называют статической, а ошибку при переходных режимах – динамической.

Текущая ошибка отработки переменного сигнала называется динамической ошибкой САУ. Динамическая ошибка системы изменяется с течением времени. Она зависит от структуры, параметров и характера изменения воздействий САУ.

38 Повышение качества и синтез линейных сау

В системе регулирования по отклонению установившаяся [ошибка имеет три составляющие:

(⁵-²⁴)

| где — ошибка воспроизведения задающего воздействия — ошибка, вызываемая действием возмущений; — ошибка чувствительного элемента, измеряющего рассогласование

Как было показано в гл. 4, установившаяся ошибка может [быть представлена в виде ряда (4.3). При этом коэффициенты [ошибок воспроизведения вычисляют по передаточной функции замкнутой системы для ошибки вос­произведения

Нужно, заметить, что в статической системе

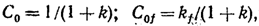
где k — передаточный коэффициент разомкнутой системна; — передаточный коэффициент прямой, цепи от возмущения до выходной координаты у.

Следовательно, уменьшение установившейся ошибки постоянных значениях задающего воздействия и возмущения достигается увеличением передаточного коэффициента разом­кнутой системы. Однако с увеличением статической точности в большинстве случаев уменьшаются запасы устойчивости I и при значительном увеличении k система становится неустойчи­вой.

Противоречие между статической точностью и устойчиво­стью проиллюстрировано на рис. 5.9, где сплошными линиями показаны логарифмические частотные характеристики разом­кнутой системы с передаточной функцией

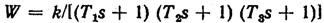
при

Если пере­даточный коэффициент увеличить до k — 60, то ЛАЧХ при­нимает положение, показанное пунктиром. Частота среза уве­личилась и запас устойчивости по фазе уменьшился с до Столь малый запас по фазе совершенно недопустим.

При повышении статической точности путем увеличения передаточного коэффициента k разомкнутой системы необхо­димы мероприятия для обеспечения достаточного запаса устой­чивости. Они будут рассмотрены в следующем параграфе. Воз­можно, вообще говоря, создание такой структуры системы, ко­торая допускает неограниченное увеличение передаточного коэффициента k разом­кнутой цепи 121.

Другой путь повы­шения статической точ­ности — обеспечение астатизма. В астатической системе младшие коэф­фициенты ошибки имеют следующие значения:

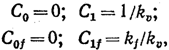
где k₀ — передаточный ко­эффициент разомкнутой системы называемый в данном случае добротно­стью системы по скорости (или коэффициентом доб­ротности по скорости). Таким образом, в астатической системе отсутствует уста­новившаяся ошибка от постоянного задающего воздействия и постоянных возмущений.

Для астатизма относительно возмущения интегрирующее звено должно быть введено до точки, в которой приложено возмущение (рис. 5.10).

Влияние интегрирующего звена на динамические свойства системы где сплошными линиями пока­заны логарифмические частотные характеристики системы с пе­редаточной функцией (5.26). При введении в разомкнутую цепь этой системы интегрирующего звена характеристики прини­мают положение, показанное пунктиром. Фазочастотная харак­теристика переместилась вниз на —90°, а амплитудно-частот­ная характеристика повернулась вокруг точки а по направле­нию часовой стрелки . В результате запас устойчивости по фазе уменьшился с до недопустимо малого значения Система остается устойчивой, но переходный процесс будет сильно колебательным. Кроме того, уменьшилась ча­стота среза и переходные процессы будут более продолжитель­ными.

Однако в других ситуациях введение интегрирующего зве­на может не только не ухудшить, а даже улучшить динамиче­ские свойства системы. Пусть, например, посто­янные времени системы с передаточной функ­цией (5.26) имеют сле­дующие значения: Т₁ = = 0,05 с, Т₂ = 0,0025 с и T₃ = 0,001 с. Лога­рифмические частотные характеристики разомк­нутой системы показаны

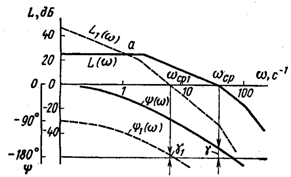
При введе­нии интегрирующего звена характеристики принимают положе­ние, показанное пунк­тирными линиями. В данном случае ин­тегрирующее звено уменьшило частоту среза, но запас устой­чивости по фазе увеличился с |до . Хотя быстродействие системы уменьшилось, но уменьшилась и колебательность.

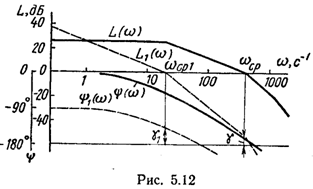
Таким образом, при повышении статической точности путем введения интегрирующего звена могут оказаться необхо­димыми мероприятия по сохранению запасов устойчивости САУ.

Значительно лучшие результаты получают при получении астатизма с помощью изодромного звена, т. е- звена с передаточной функцией

постоянная времени изодрома.

Если постоянная времени достаточно велика, то запас устойчивости может быть сохранен неизменным. Уменьшение передаточного коэффициента разомкнутой системы должно быть скомпенсировано увеличением коэффициента усиления усилителя. Следует учитывать, что при большом значении могут увеличиться старшие коэффициенты ошибки.

Астатизм САУ относительно задающего воздействия можно обеспечить более простыми способами: неединичной обрат­ной связью и масштабированием [3).

Структурная схема системы с неединичной обратной свя­зью показана на рис. 5.13, а. В установившемся режиме регу­лируемая координата связана с постоянным задающим воздей­ствием соотношением

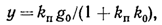(5.27)

где k_n — передаточный коэффициент прямой цепи системы.

Если выполнить основную обратную связь системы с коэффициентом и система относитель­но задающего воздействия будет астатической.Структурная схема системы масштабированием входной (величины показана на рис. 5.13, б. Ее особенность — наличие

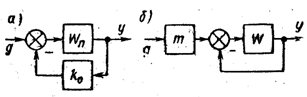
усилительного звена с передаточным ко­эффициентом m на входе. В установив­шемся режиме

где k — передаточный коэффициент разомкнутой системы.

При /л = 1 -f- УЬ получаем у = g₀ и система является аста­тической относительно задающего воздействия.

Недостаток этих способов в том, что астатизм обеспечива­ется только при сохранении указанных соотношений между пе­редаточными коэффициентами. Неточное определение переда­точного коэффициента какого-либо элемента системы и его изменение в процессе эксплуатации ведут к появлению стати­ческой ошибки. Астатизм, достигнутый введением интегрирую­щего или изодромного звена, сохраняется и при изменении па­раметров системы. Однако нужно иметь в виду, что введение двух интегрирующих звеньев в систему, состоящую из усили­тельных, апериодических и колебательных звеньев, сделает ее структурно-неустойчивой. Возможно обеспечение астатизма и более высокого порядка. При этом из-за введения большого числа интегрирующих или изодромных звеньев и мероприятий, обеспечивающих требуемые динамические свойства, структура САУ значительно усложняется.

Компенсация внешнего воздействия (обеспечение инвари­антности). Рассмотренные выше способы улучшения статиче­ских и динамических свойств системы связаны лишь с изме­нениями параметров элементов САУ и структуры ее отдельных участков, но при этом не затрагивают принципа действия си­стемы.

Помимо принципа регулирования по отклонению сущест­вует принцип регулирования по внешнему воздействию. Значительный эффект дает их одновременное ис­пользование. В этом случае системы называются комбиниро­ванными. Кроме замкнутого контура они имеют дополнитель­ную цепь влияния внешнего воздействия — возмущения или задающего.