
- •32 Анализ качества управления.
- •33 Корневые методы оценки качества сау.
- •34 Оценка качества регулирования при гармонических воздействиях
- •35 Интегральный метод анализа качества сау.
- •36 Частотный метод анализа качества сау.
- •37 Статические и динамические ошибки.
- •38 Повышение качества и синтез линейных сау
- •39 Коррекция сау с помощью дифференцирующих, интегрирующих и интегро - дифференцирующих устройств.
- •Коррекция с помощью дифференцирующих устройств.
- •Коррекция с помощью интегрирующих устройств.
- •40 Последовательное корректирующее устройство
- •42 Использование обратных связей для повышения качества.
- •43 Понятие желаемой лачх, методика ее построения.
- •44 Синтез корректирующих устройств по лачх
- •45, 46 Теория инвариантности
36 Частотный метод анализа качества сау.
Данный метод основан на основе преобразования Лапласа и интеграла Фурье, которые позволяют установить связь между переходным процессом и частотными характеристиками САУ. При этом также открывается возможность оценить качественные показатели переходного процесса, если заданы или определены частотные характеристика разомкнутой и замкнутой систем. Кроме того данный метод позволяет выполнить графоаналитическое построение переходного процесса без вычисления корней характеристического уравнения.
Рассмотрим зависимость между переходным процессом и вещественной частотной характеристикой САУ.
Пусть некоторая замкнутая САУ обладает передаточной функцией Ф(р). Если на её вход поступает сигнал, изображение которого равно G(р), то можем записать выходную величину этой САУ.
![]() (1)
(1)
Используя преобразования Лапласа, запишем переходный процесс в следующем виде:
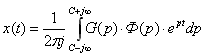 (2)
(2)
Если данная система устойчива, то полюсы её характеристического уравнения на комплексной плоскости расположены слева. В этом случае интегрирование по формуле (2) можно осуществить вдоль мнимой оси приняв С = 0.
Оператор
Лапласа р при этом можем заменить на
мнимую переменную в частотной области
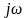 ,
осуществив тем самым переход к интегралу
Фурье с помощью которого установится
связь между переходным процессом и
частотными характеристиками.
,
осуществив тем самым переход к интегралу
Фурье с помощью которого установится
связь между переходным процессом и
частотными характеристиками.
Для более подробного анализа рассмотрим случай когда на вход САУ поступает единичный скачкообразный сигнал, изображение которого равно 1/р.
На базе выражения (2), тогда можем записать:
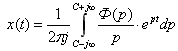 (3)
(3)
Предположим, что в замкнутом состоянии эта САУ устойчива, а её корни левые. Изображение переходной функции по Лапласу однако при этом будет иметь один полюс первого порядка в начале координат, следовательно в формуле (3) нельзя принять С=0 как в предыдущем случае.
Для устранения этого затруднения в изображении Ф(р) выделим ту часть, которая определяется полюсом, расположенным в правой полуплоскости и на мнимой оси. Поскольку в данном случае мы имеем один простой полюс в начале координат, обусловленный воздействием, то применение правила разложения дробно рациональной функцией на простые дроби с определением коэффициента, разложение даёт возможность записать:
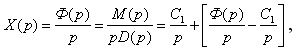
где С1 определяется следующим отношением:
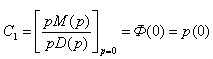 (4)
(4)
С1 – та часть изображения, которая обусловлена одним полюсом на мнимой оси.
Далее представив выражение (4) в выражение (3) можем записать:
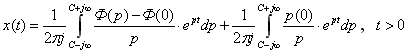 (5)
(5)
Анализируя
выражение (5) можем установить, что
изображение в первом слагаемом под
интегралом
![]() имеет полюсы согласно выражению (4),
расположены только в левой полуплоскости.
В следствии этого в первом интеграле
выражения (5) можем принять С=0
и интегрирование осуществить вдоль
мнимой оси. Это позволяет заменить р
на
имеет полюсы согласно выражению (4),
расположены только в левой полуплоскости.
В следствии этого в первом интеграле
выражения (5) можем принять С=0
и интегрирование осуществить вдоль
мнимой оси. Это позволяет заменить р
на
![]() и перейти к интегралу Фурье.
и перейти к интегралу Фурье.
Второе слагаемое в выражении (5) представляет собой обратное преобразование Лапласа для постоянной величины Р(0).
С учётом изложенного выше выражение (5) можем привести к следующему виду:
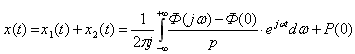 (6)
(6)
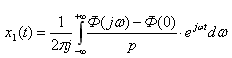 (7)
(7)
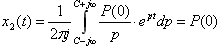 (8)
(8)
Будем
учитывать, что АФХ замкнутой системы
![]() может быть выражена через вещественную
и мнимую частотные характеристики с
учётом того что
может быть выражена через вещественную
и мнимую частотные характеристики с
учётом того что
![]() можно разложить в
можно разложить в
![]() .
.
Отбросим
мнимую часть в
![]() ,
которая тождественно равна 0 и выражение
(7) перепишем в виде:
,
которая тождественно равна 0 и выражение
(7) перепишем в виде:
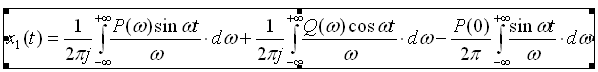 (9)
(9)
Т.к.
![]() и
и
![]() в
являются чётными функциями относительно
частоты, а
в
являются чётными функциями относительно
частоты, а
![]() являются нечётными относительно частоты,
установим что в выражении (9) все
подынтегральные функции чётные. Интеграл
от чётной функции в бесконечных пределах
может быть заменён удвоенным интегралом
от той же функции, но в пределах
являются нечётными относительно частоты,
установим что в выражении (9) все
подынтегральные функции чётные. Интеграл
от чётной функции в бесконечных пределах
может быть заменён удвоенным интегралом
от той же функции, но в пределах
![]()
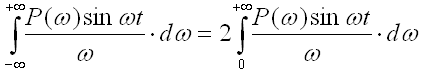
Кроме того последний интеграл в правой части выражения (9) называют интегральным синусом, который можно преобразовать следующим образом:
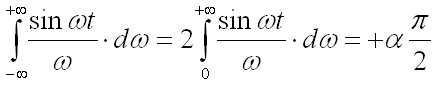
С учётом преобразований запишем:
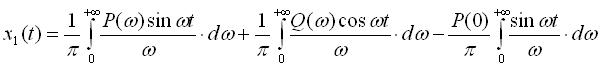 (10)
(10)
При
![]() переходная функция
переходная функция
![]() а также процессы
а также процессы
![]() равны 0. Если в уравнении (10) произвести
замену t
на –t,
то получим:
равны 0. Если в уравнении (10) произвести
замену t
на –t,
то получим:
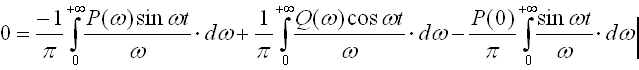 (11)
(11)
Вычтем из уравнения (10) выражении (11), а затем просуммировав указанные выражения, получим две зависимости:
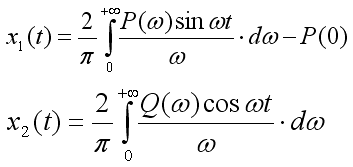
Если
в данные уравнения поочерёдно подставить
в выражение (6), то получим для
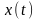 окончательную формулу через вещественную
и мнимую частотную характеристики.
окончательную формулу через вещественную
и мнимую частотную характеристики.
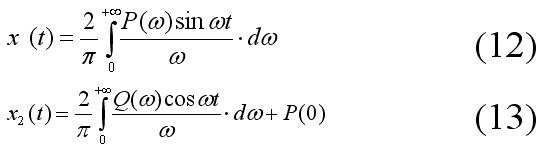
Уравнение
(12) устанавливает связь между переходной
функцией
![]() и вещественной характеристикой
и вещественной характеристикой![]() ,
а уравнение (13) – между переходной
функцией
и мнимой частотной характеристикой.
,
а уравнение (13) – между переходной
функцией
и мнимой частотной характеристикой.
Т.о.
чтобы вычислить переходный процесс по
одной из полученных зависимостей
достаточно знать![]() .
Однако их аналитическое задание не
всегда возможно, но даже в тех ситуациях,
когда их точное математическое описание
известно, вычисление интегралов (12) или
(13) можно производить графоаналитическим
методом.
.
Однако их аналитическое задание не
всегда возможно, но даже в тех ситуациях,
когда их точное математическое описание
известно, вычисление интегралов (12) или
(13) можно производить графоаналитическим
методом.
Следует также учитывать, что выражение (12) и (13) справедливы только при единичном скачкообразном воздействии подаваемом на вход замкнутой САУ. Однако методика их вывода аналогична и может быть использована при уст. Связей между переходным процессом и частотными характеристиками при воздействии другого вида подаваемых на вход САУ.
Рассмотрим ряд оценочных качеств процессов в САУ при их частотном анализе.
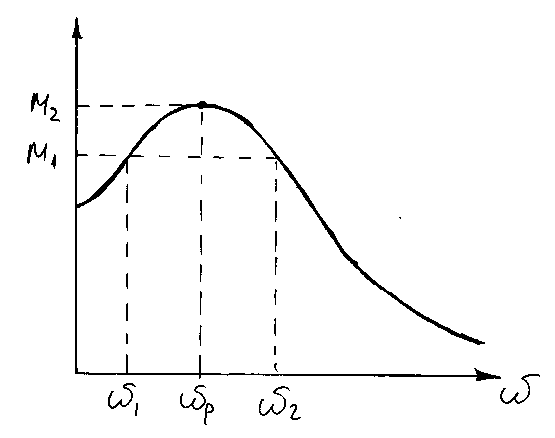
Показатель колебательности М – это отношение наибольшего значения модулей частотной передаточной функции замкнутой САУ к значению модуля частотной передаточной функции при частоте
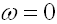 .
.
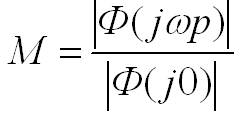
![]() частота
при которой частотная передаточная
функция достигает своего максимального
значения.
частота
при которой частотная передаточная
функция достигает своего максимального
значения.
Рассмотрим зависимость динамических свойств САУ от величины показателя колебательности. Для этого найдём связь между величиной показателя колебательности и расположением нулей и полюсов передаточной функции замкнутой системы. Как известно динамические свойства САУ в основном определяются двумя – тремя плюсами и одним – двумя нулями передаточной функции замкнутой системы. Пусть передаточная функция замкнутой системы имеет 2 комплексно – сопряжённых корня и описывается следующим выражением:

Через параметры передаточной функции можем записать перерегулирование:
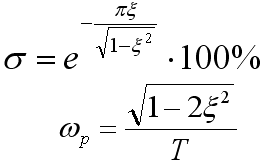
Подставим
выражение
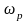 в выражение для колебательности, запишем:
в выражение для колебательности, запишем:
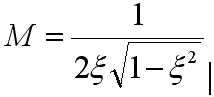
Полученные
выражения позволяют установить, что
параметр колебательности М и
перерегулирование
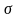 ,
зависят от коэффициентов демпфирования
из передаточной функции замкнутой
системы. Полученные выражения позволяют
графически установить связь между
перерегулирование и колебательностью:
,
зависят от коэффициентов демпфирования
из передаточной функции замкнутой
системы. Полученные выражения позволяют
графически установить связь между
перерегулирование и колебательностью:
![]()
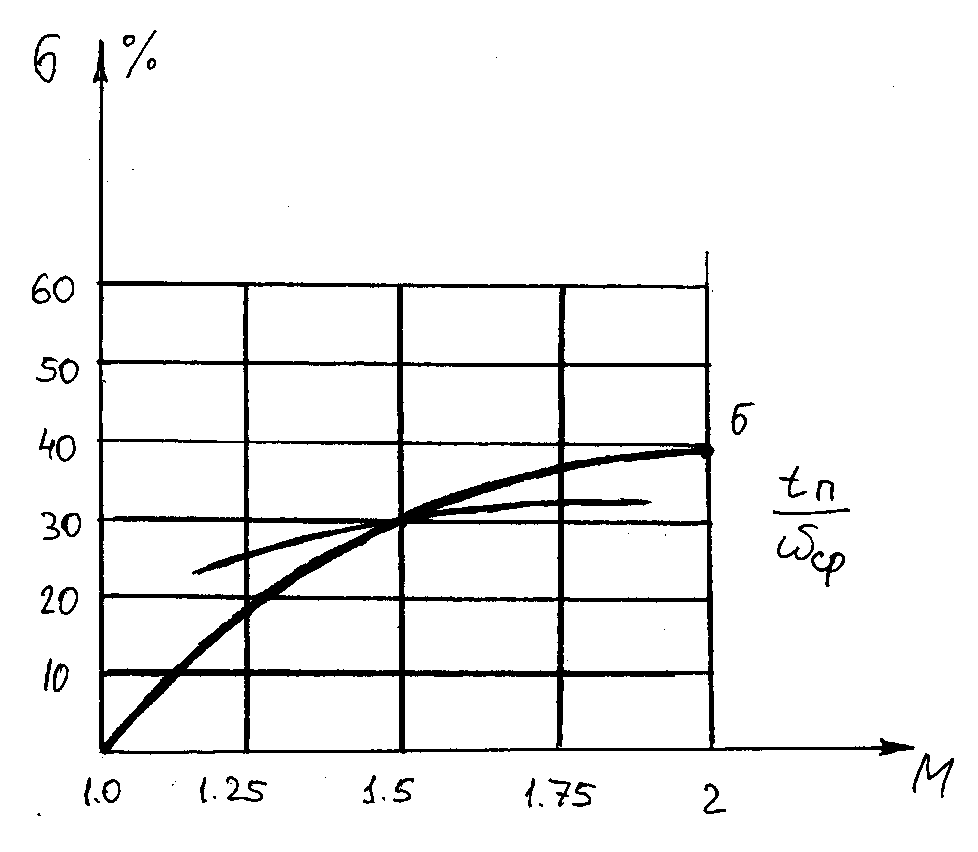
Ранее
было также установлено и показано, что
добавление в числитель передаточной
функции выражения
![]() на комплексной плоскости даёт ещё один
ноль
на комплексной плоскости даёт ещё один
ноль![]() ,
который будет увеличивать перерегулирование.
С учетом последней зависимости очевидно,
что при этом будет возрастать показатель
колебательности. Ранее было также
установлено, что добавлении в знаменатель
передаточной функции сомножителя
,
который будет увеличивать перерегулирование.
С учетом последней зависимости очевидно,
что при этом будет возрастать показатель
колебательности. Ранее было также
установлено, что добавлении в знаменатель
передаточной функции сомножителя
![]() даёт на комплексной плоскости третий
полюс р3
равный
1/T,
который будет способствовать уменьшению
перерегулирования при это произойдёт
и уменьшение параметра колебательности.
даёт на комплексной плоскости третий
полюс р3
равный
1/T,
который будет способствовать уменьшению
перерегулирования при это произойдёт
и уменьшение параметра колебательности.
Подобным образом установим связь между параметром колебательности М и быстродействии САУ.
Для систем, параметры колебательности которых лежат в диапазоне:
М: 1, 2.. существует зависимость:
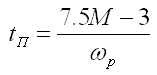
Учитывая
что![]() ,
можно записать:
,
можно записать:
![]()
Чем
больше
![]() разомкнутой системы, тем в большем
диапазоне частот система пропускает
гармонические колебания.
разомкнутой системы, тем в большем
диапазоне частот система пропускает
гармонические колебания.
Полоса пропускания такой САУ будет больше чем больше частота среза, тем меньше времени переходного процесса. Однако, частоту разомкнутой системы и следовательно её полосу пропускания нельзя выбирать чрезмерно большой, т.к. при этом будет увеличиваться ошибка САУ от сигнала помехи.
