34 Оценка качества регулирования при гармонических воздействиях

При гармонических воздействиях качество системы приня­то оценивать по амплитудно-фазовой, амплитудно-частотной, фазочастотной и логарифмическим частотным характеристи­кам. Для оценки качества переходного процесса используются следующие величины: показатель колебательности М, ре­зонансная (собственная) частота w_р, полоса пропускания си­стемы w₀, частота среза w_ср, запасы устойчивости по модулю и по фазе.

Показатель колебательности М — это отношение макси­мального значения амплитудно-частотной характеристики A_зmах(w) замкнутой системы к ее значению при w = 0 (рис. 4.5):

при А₃ (0) = 1 показатель колебательности М — A_зmaх(w).

Показатель колебательности характеризует склонность си­стемы к колебаниям. Чем выше М, тем менее качественна система при прочих равных условиях. Считается допустимым, если 1,1 М 1,5.

Частоту w_р, при которой - аплитудночастотная характеристика замкнутой САУ имеет максимум, называют резо­нансной частотой системы (рис. 4.5); на этой частоте гармонические колебания проходят через систему с наибольшим усиле­нием.

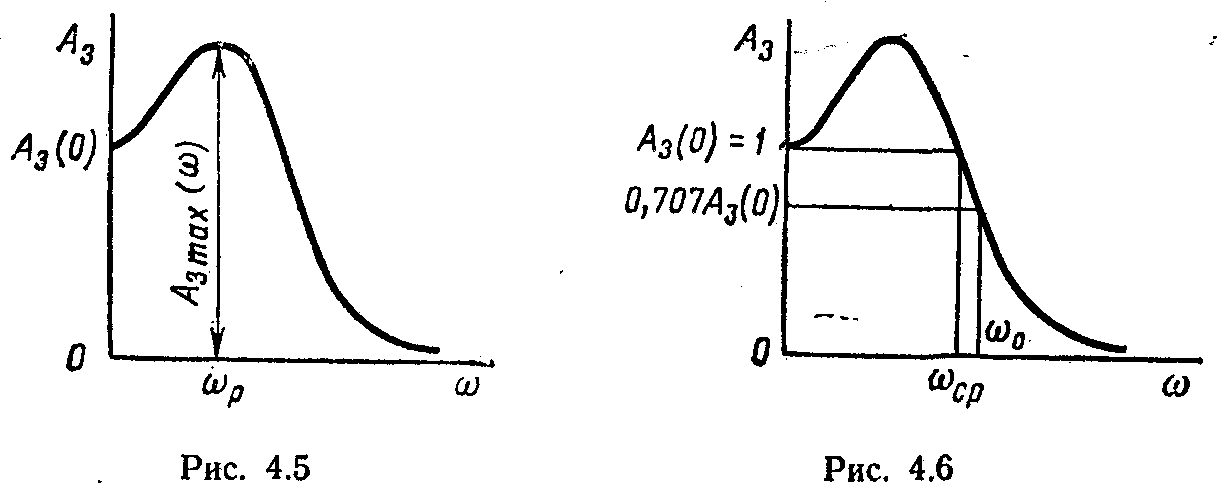
Полоса пропускания системы (рис. 4.6) — это интервал частот от w = 0 до w₀, при котором выполняется условие

или при А_а (0) = 1 величина А₃ (w₀) <=0,707. Полоса про­пускания не должна быть слишком широкой, иначе система будет воспроизводить высокочастотные помехи.

Частота среза w_ср — частота, при которой амплитудно-частотная характеристика системы принимает значение, рав­ное 1, т. е. А₃ (w_ср) =1. Эта частота косвенно характеризует длительность переходного процесса. Время регулирования обратно пропорционально частоте среза:

Если переходный процесс имеет одно - два колебания, то время достижения переходной характеристикой первого максимума

Склонность системы к колебаниям характеризуется вели­чинами ее запасов устойчивости по модулю и по фазе, опреде­ление которых дано в предыдущей главе. В хорошо демпфи­рованных системах запас устойчивости по амплитуде колеблет­ся в пределах от 6 до 20 дБ, а запас по фазе — от 30 до 60°.

Так как рассмотренные выше показатели косвенно опреде­ляют быстродействие, перерегулирование и т. п., то их исполь­зуют и для расчета систем, находящихся под воздействием не­периодических возмущений.

35 Интегральный метод анализа качества сау.

Как было показано выше, кривая переходного процесса позволяет оценить качество процесса происходящего в данной системе. При этом косвенную оценку качества регулирования можно производить путем вычисления площади, заключенной между кривой переходного процесса и линией установившегося режима. Критерием качества также является определенный интеграл по времени от функции, характеризующей разность между действительным и заданным значением координат систем. Этот определенный интеграл называется интегральной оценкой САУ. В таком виде интегральная оценка используется главным образом для анализа монотонных процессов. Для расширения областей применения интегральной оценки в рассмотрение часто вводят интеграл от квадратичной формы координат системы. Вследствие этого под интегральной оценкой в более общем случае понимают определенный интеграл от функции, которая определяет состояние системы и характеризуется в различных комбинациях системными координатами, а также их производными. В этом случае качество САУ оценивается по минимуму интегральной оценки. Различают линейные и квадратичные интегральные оценки.

Рассмотрим линейные интегральные оценки. Линейной интегральной оценкой называют определенный интеграл от линейной функции координат системы.

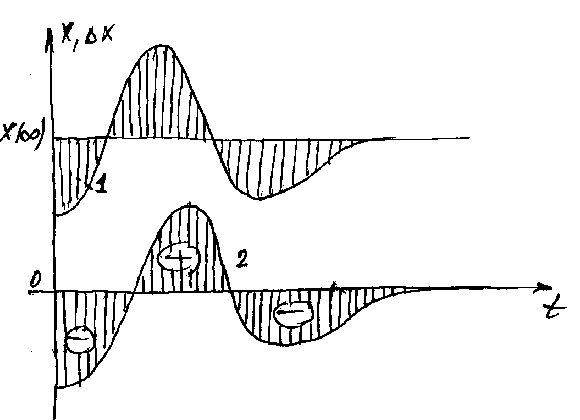
Для данной характеристики интегральная оценка имеет следующий вид:

.

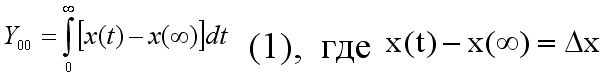Интеграл (1) определяет площадь ограниченную переходным процессом (кривая (1)) и линией установившегося режима или площадь заключенную между кривой (2) и осью времени.

Способ определения интеграла (1) основан на применении преобразований Лапласа.

.

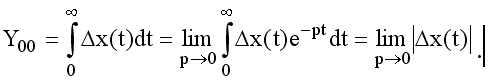Будем рассматривать переходный процесс в САУ как реакцию на ступенчатое воздействие.

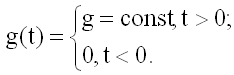
При нулевых начальных условиях запишем изображение:

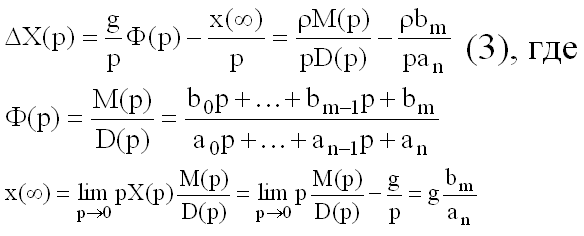
Используя уравнения (2) и осуществив предельный переход в уравнения (3) найдем интегральную оценку

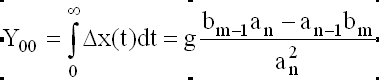(4).

Используя данную методику можно вычислить интегральную оценку САУ вида (1) и соответственно не при нулевых начальных условиях. Анализируя выражения (4), установим, что величина интегральной оценки зависит от значения коэффициентов дифференциальных уравнений и, следовательно, от значений рабочих параметров САУ. При этом параметры САУ следует выбирать по минимуму оценки вида (4), который имеет место при выполнении равенства: . Такой подход дает правильный результат в случае монотонных процессов.

В случае, когда процессы носят колебательный характер, вычисление интеграла вида (1) вследствие алгебраического суммирования площадей, ограниченных кривой 2 и осью времени может указать на существование минимума интегральной оценки, хотя колебания в системе будут иметь затухающий характер. Данный факт можно объяснить тем, что обращение в ноль оценки вида (4) еще не означает приближение переходного процесса к желаемому виду. В этом случае для получения правильного результата необходимо использовать дополнительные критерии (например, критерий апериодичности). Эта особенность интегральной оценки является ее недостатком, существенно ограничивающим область ее применения. К линейным интегральным оценкам кроме описанных выше относят следующие виды интегральных оценок:

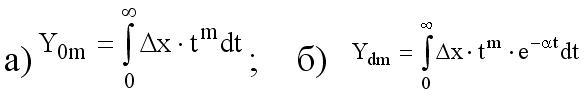
Интегральные оценки вида а) можно привести к следующему интегралу:

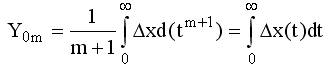, который определяется площадью кривой и осью времени .

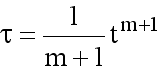С уменьшением этой площади качество процесса уменьшается, но для колебательного процесса интегральная оценка не может служить мерой быстроты затухания колебаний регулируемой величины. Далее рассмотрим квадратичные интегральные оценки.

В ТАУ постоянная, имеющая размерность времени. Проведем анализ уравнения (1). Данная квадратичная оценка может быть использована для любых процессов, т. к. в рассмотрение принимаются только квадратичные значения ординаты переходного процесса и вычисляется площадь кривой (1): . При этом из нескольких процессов наиболее качественным считается тот, который соответствует наименьшему значению интегральной оценки. Наименьшую интегральную оценку можно получить, используя вычисление обратного преобразования Лапласа. При этом будем использовать метод, предложенный академиком Мандельштамом, основанный на приближении дифференциального уравнения, соответствующего установившейся системе:

.

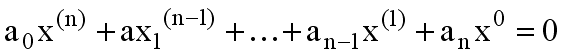Будем считать, что все производные выходной величины и сама величина x при превращаются в ноль.

.

Проинтегрируем полученное уравнение и будем учитывать обозначение квадратичных оценок и получим систему интегрированных

Далее запишем систему из n уравнений следующего вида

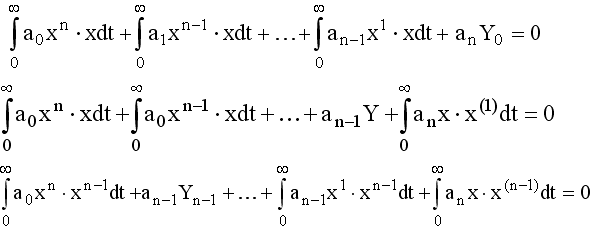
В данном уравнении интегралы вычисляются по частям до конкретного результата или до тех пор пока не получится одна из интегральных оценок.

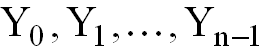
Система уравнений после интегрирования может быть использована для определения неизвестных квадратичных оценок, число которых равно числу уравнений, входящих в систему. Далее используем преобразование Лапласа, при этом в рассмотрение вводят изображение регулируемой величины.

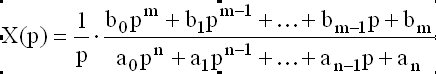
Кросовским было доказано, что при m<n квадратичная оценка может быть вычислена по следующей формуле:

определитель, который получается из матрицы путем замены k+1 столбца столбцом

Определитель соответствует старшему определителю Гурвица. При его составлении все коэффициенты с отрицательным индексом и индексами большими n заменяются нулями. Аналогичная замена нулями коэффициентов с индексами, меньшими нуля и большими n

осуществляется при нахождении .

При нахождении САУ на границе устойчивости, когда определитель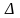 обращается в ноль, квадратичная оценка бесконечно возрастает. Квадратичные интегральные оценки используют для выбора параметров САУ, обеспечивающих оптимум переходного процесса, соответствующих минимумам интегральной квадратичной оценки.

Данный метод расчета имеет ряд недостатков. Параметры, выбранные по минимуму интегральной квадратичной оценки, могут соответствовать достаточно высокой степени колебательности процессов в САУ. На рисунке показаны кривые (1) и (2). Очевидно, что площадь, ограниченная кривой (1) будет меньше площади, ограниченной кривой (2).

При этом, график (1) соответствует процессу с большей колебательностью, чем для кривой (2).