45, 46 Теория инвариантности

В процессе управления на систему автоматического управления всегда действуют различного рода возмущения, которые вызывают нежелательные отклонения регулируемой величины от заданного значения. Назначение системы управления и заключается в том, чтобы управляя, противодействовать возмущениям на регулируемую величину.

Профессор Г.В. Щипанов сформулировав идею полной компенсации возмущений. Рассмотрим способ изложения на примере системы управления, приведенной на рис. 6.1.

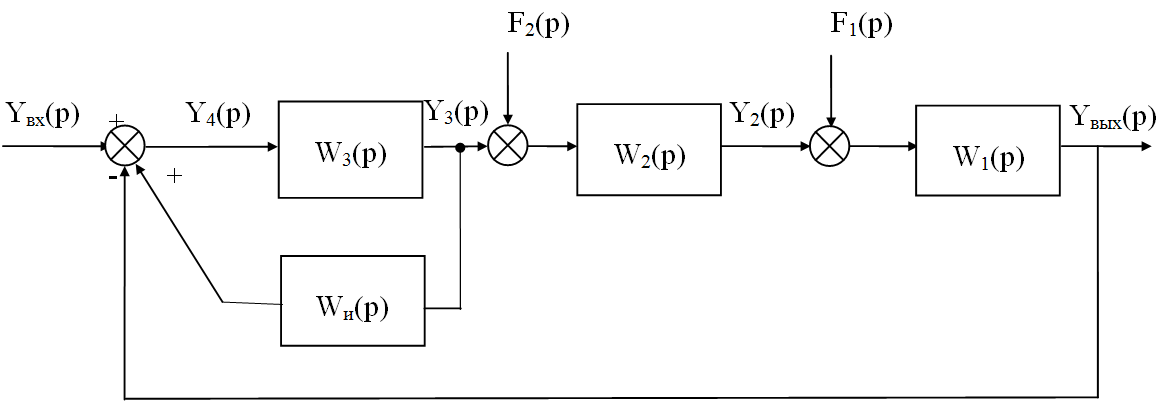
Рис. 6.1. Структурная схема САУ, инвариантной относительно возмущений F₂(p) и

F₁(p)

Составим уравнения в изображениях по Лапласу указанной системы автоматического управления:

Y_вых(p)=W₁(p)(Y₂(p)+F₁(p));

Y₂(p)=W₂(p)(Y₃(p)+F₂(p)); (6.1)

Y₃(p)=W₃(p)Y₄(p);

Y₄(p)=Y_вх(p)-Y_вых(p).

В векторно-матричной форме, эти уравнения имеют вид:

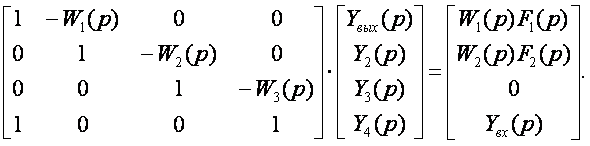
(6.1)

Очевидно, что

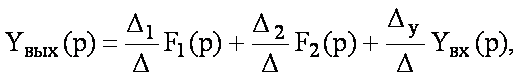
где  - главный определитель системы уравнений (6.2), ₁, ₂ и _у - определители, полученные из главного определителя путем замены соответственно элементов первого столбца коэффициентами при F₁(p), F₂(p) и Y_вх(р).

Очевидно, что условиями полной компенсации возмущений являются требования

₁=0; ₂=0 (6.3)

при сохранении управляемости системы, когда

_у0, 0. (6.4)

Г.В. Щипанов предложил ввести в алгебраическое дополнение А₁₁ элемент -а₄₃=-W_и(p), что равнозначно введению положительной обратной связи, изображенной на рис. 6.1 штрихпунктирной линией. Тогда

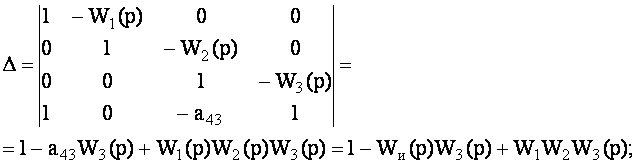
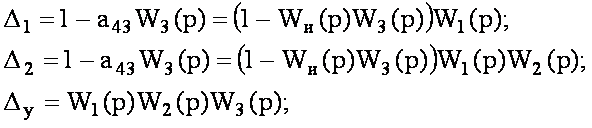(6.5)

Очевидно, что условия полной компенсации возмущений F₁(p) и F₂(p) (6.3) при сохранении управляемости (6.4) выполняются, если ₁=1-W_и(p)W₃(p)=0 или

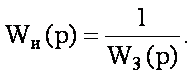(6.6)

Но физически условие (6.6) невыполнимо, так как это равнозначно включению в систему звена с бесконечно большим коэффициентом усиления, что сразу же входит в противоречие с устойчивостью системы. Действительно, эквивалентная передаточная функция W_э(р) звена W_з(р), охваченного положительной обратной связью W_и(р), равна

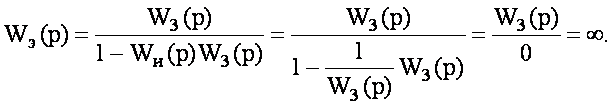
(6.7)

Таким образом, идея полной компенсации возмущений в той форме, в которой ее предложил Г.В. Щипанов, просто невыполнима.

Эта проблема явилась в дальнейшем предметом исследований математиков а также специалистов по теории автоматического управления, которые назвали идею полной компенсации возмущений или теорией инвариантности. Полная компенсация возмущений равносильна достижению полной независимости - инвариантности регулируемой величины от возмущений. Большое значение для дальнейшего развития теории инвариантности получил разработанный Б.Н. Петровым принцип двухканальности [20]. Им показано, что только при соблюдении этого принципа возможна полная инвариантность регулируемой величины от возмущений.

Рассмотрим на примере системы, приведенной на рис. 6.1, как может быть осуществлен принцип двухканальности (рис. 6.2).

На рис.6.2 второй канал для распространения возмущения F₂(p), действующего на регулируемую величину Y_вых(p) изображен штрихпунктирной линией. В уравнении системы (6.2) это равнозначно добавке в матрицу слева элементов a₁₃=-W_и(p)W₁ и a₄₂=1.

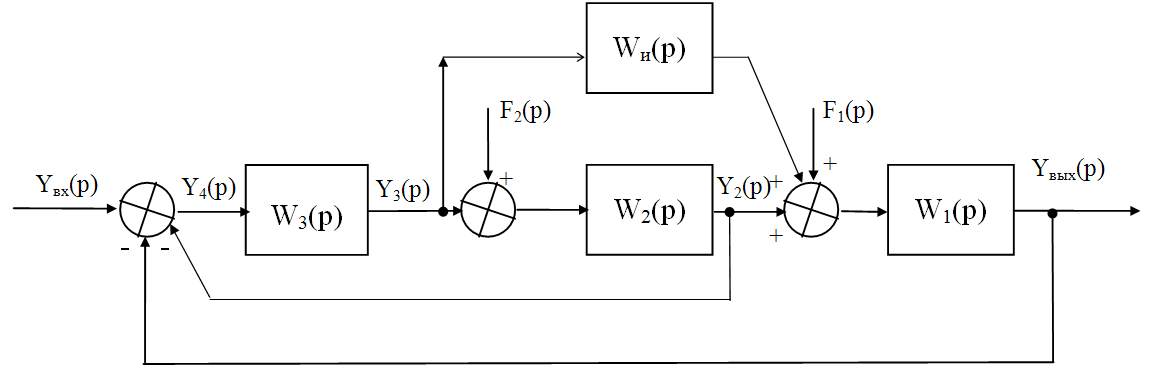
Рис. 6.2. Двухканальная инвариантная система автоматического управления

Тогда решение уравнения (6.2) с добавкой в матрице элементов а₁₃ и а₄₂ равно:

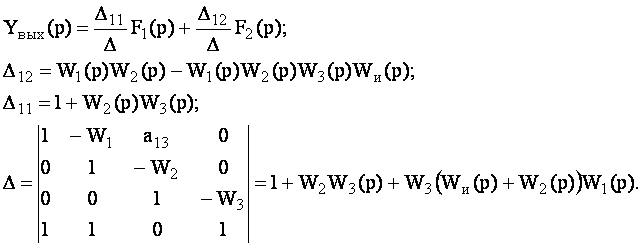
(6.8)

Если в уравнении (6.8) предположить, что

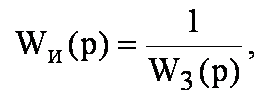(6.9)

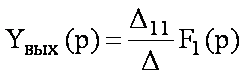то ₁₂  0, и не зависит от F₂, а условие (6.9) не вступает в противоречие с устойчивостью. Но ₁₁0, т.е. компенсации возмущения F₁(p) при этом не получается.

Дальнейшая разработка теории инвариантности показала, что не всегда идея полной компенсации возмущений может быть физически реализована. Но там, где это можно осуществить, удается получить системы высокого качества.