32 Анализ качества управления.

Анализ качества управления линейных САУ.

Любая САУ должна быть не только устойчивой, но и обладать достаточным качеством процессов. Одной из характеристик качества управления является точность САУ, которую количественно принято оценивать по величине ошибки САУ при различных воздействиях. В любой реальной САУ невозможно точное равенство задающего воздействия g и управляемой величины y. Ошибка САУ при этом вычислим согласно уравнению ошибки как разность этих воздействий, т.е.:

Учитывая историю переходных процессов, ошибку можно представить в виде двух составляющих: установшейся и переходной:

В линейных САУ установившаяся ошибка определяется частным решением её дифференциального уравнения, а переходная ошибка – решением однородного дифференциального уравнения.

Рассмотрим методы определения ошибки в установившихся и переходных режимах.

1. Режим неподвижного состояния

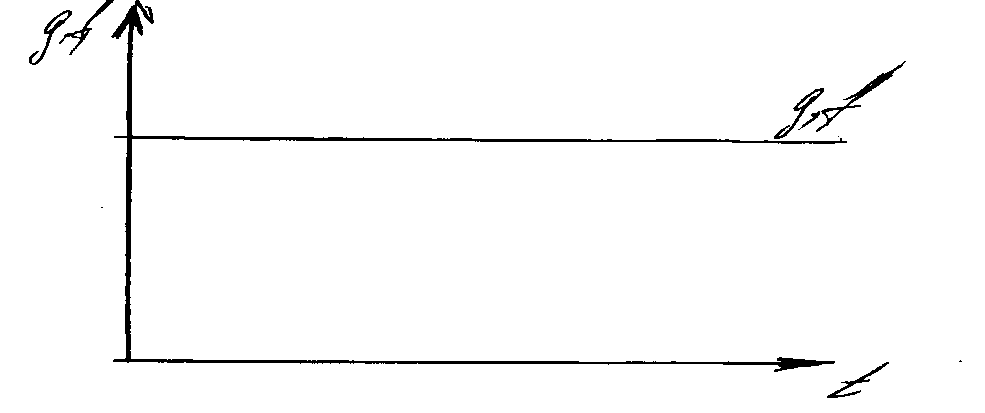
g и f изменяются по приведённому закону, т.е. остаются постоянными величинами во всё время процесса управления.

Рассмотрим определение ошибки в статической с САУ с единичной обратной связью:

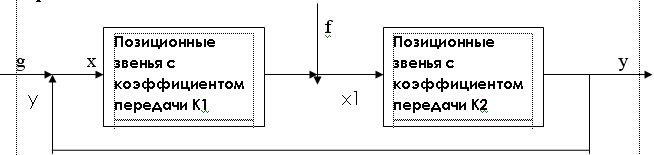
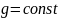
По окончанию переходного процесса, при и 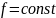постоянной будет и выходная координата устойчивой САУ.

В этом случае ошибка САУ х так же будет постоянной. Запишем установившуюся ошибку САУ под цифрой 1.

(1)

Общеизвестно, что установившееся значение выходной координаты позиционного звена при постоянном входном сигнале прямо пропорционально входному сигналу и коэффициенту передачи этого звена:

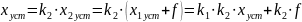(2)

Подставив (2) в (1) запишем:

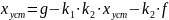
Из полученного выражения получим:

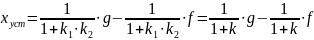(3)

где

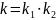
Часто установившуюся ошибку САУ в неподвижном состоянии называют статической и обозначают .

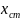Анализируя полученное выражение (3) можно установить, что с целью уменьшения статической ошибки от задающего воздействия, необходимо увеличивать общий коэффициент передачи разомкнутой САУ. Для уменьшения статической ошибки от возмущающего воздействия необходимо увеличивать коэффициент передачи звеньев стоящих до приложении этого воздействия и уменьшить коэффициент передачи звеньев стоящих после приложения этого воздействия.

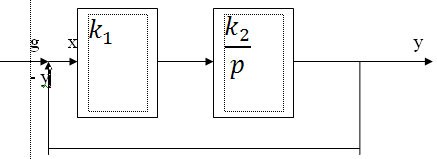
Рассмотрим определение статической ошибки для астатической системы первого порядка. Рассмотрим следующую структурную схему:

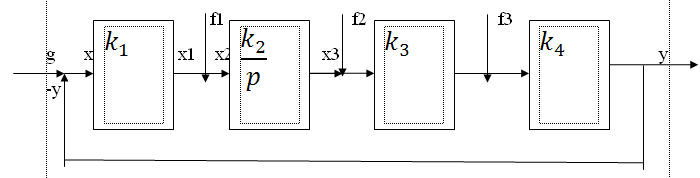
В устойчивом состоянии данной системы

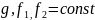
Следовательно по окончании переходного процесса постоянно будет и управляемая величина. Она будет равна у-значенью. Это обеспечивается только в том случае, если сигнал на входе интегрирующего звена равен нулю. Запишем сигнал на входе интегрирующего звена по окончанию переходного процесса:

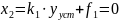
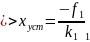
Следовательно ошибка в астатической системе в режиме неподвижного состояния зависит лишь от возмущающего воздействия, приложенного до интегрирующего звена и не зависит от задающего воздействия и возмущающих воздействий, приложенных после него.

2. Режим движения с постоянной скоростью

Будем считать постоянной скорость изменения задающего воздействия во всё время процесса регулирования.

В установившейся системе по окончании переходного процессов выходная величина должна так же изменяться с постоянно скоростью, которая будет равна скорости изменения задающего воздействия. Сигнал на выходе интегрирующего звена для этого должен изменяться с постоянной скоростью. Выходная координата интегрирующего звена изменяется с постоянной скоростью, если на входе звена действует постоянный сигнал. При постоянном сигнале на входе интегрирующего звена, выходная координата САУ будет изменяться с постоянной скоростью:

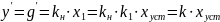
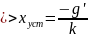
где - коэффициент передачи разомкнутой САУ

Вывод: величина установившейся ошибки напрямую зависит от скорости входного сигнала.

Выражение для ошибки останется таким же при любом расположении интегрирующего звена в прямой цепи контура управления.

При отсутствии возмущающего сигнала, отношение скорости к ошибке, называется добротностью САУ по скорости:

3. Движение САУ по гармоническому закону.

Рассмотрим следующую систему:

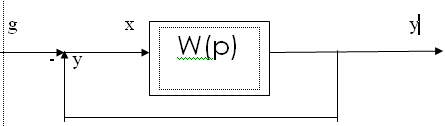
Будем считать, что на входе действует задающее воздействие g, а так же действует возмущающее воздействие f, которые изменяются по некоторому гармоническому закону. Рассмотрим несколько случаев:

а) когда к системе приложено только задающее воздействие g, изменяющееся по гармоническому закону

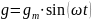
Точность САУ можно определить по амплитуде ошибки:

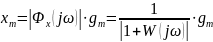
Для уменьшения действующей ошибки, параметры САУ необходимо изменять таким образом, чтобы выражение в знаменателе было 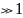. Данное условие будет выполняться, если модуль 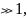тогда можно записать:

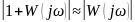
С учётом последнего выражения для точности запишем:

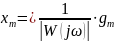
Для того чтобы точность САУ была не хуже заданной, должно выполняться следующее условие:

Данное неравенство будет выполняться , если логарифмическая амплитудно частотная характеристика разомкнутой системы на частоте 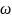проходит выше некоторой точки А, с координатами :

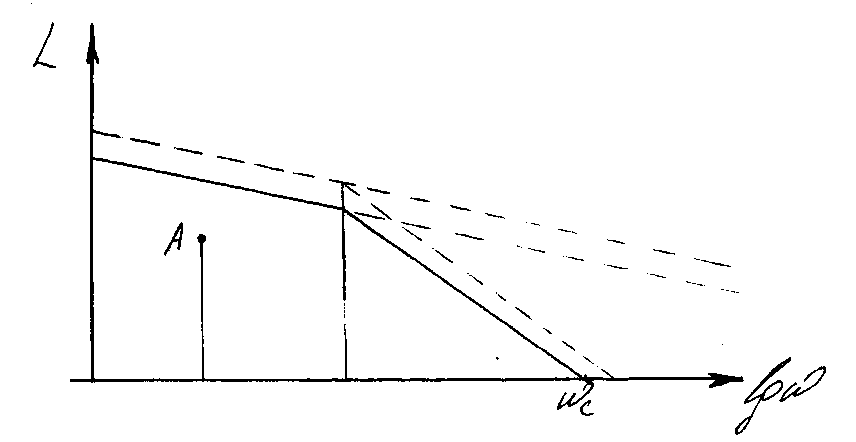
Из данного рисунка видно, что для увеличения точности САУ необходимо увеличивать общий коэффициент усиления разомкнутой системы:

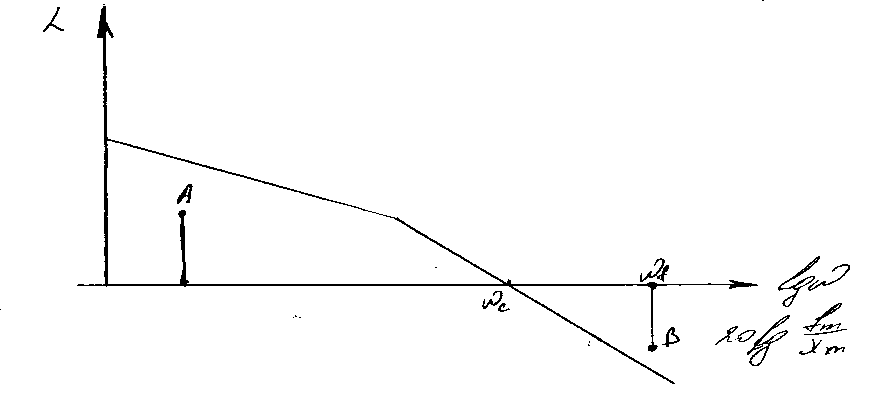
б) Рассмотрим случай, когда на входе действует сигнал помехи f. Ранее было показано, что при g=0, выходная координата y так же будет равна нулю. В этом случае выходной сигнал от действия помехи, изменяющийся по гармоническому закону будет являться ошибкой САУ.

Определим амплитуду ошибки:

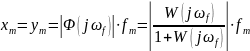
На графике ЛАЧХ 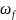обычно лежит правее 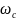разомкнутой САУ: .

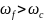В районе модуля частотной передаточной функции амплитуда ошибки будет равна:

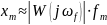
Для того чтобы ошибка системы непревосходила заданную, должно выполняться следующее условие:

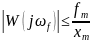
Данное условие будет выполняться, если ЛАЧХ разомкнутой системы проходит ниже точки .

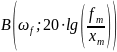Из приведённого выше рисунка можно сделать вывод, что для увеличения точности САУ полосу пропускания разомкнутой системы 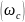необходимо уменьшать. Это снизит быстродействие, но повысит точность.