Производная параметрически заданной функции.

В
зависимости от правила, устанавливающего
зависимость между множествами значений
величин x и y,
различают несколько способов задания
функции. Наиболее привычным является
представление функции в явном виде  .
Однако, в некоторых случаях удобно
описывать функциональную зависимость
множеством пар значений (x;
y),
которые вычисляются для каждого значения
параметра t из
промежутка (a;
b).
К примеру, все пары значений
.
Однако, в некоторых случаях удобно
описывать функциональную зависимость
множеством пар значений (x;
y),
которые вычисляются для каждого значения
параметра t из
промежутка (a;
b).
К примеру, все пары значений 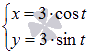 при
при  задают
окружность с центром в начале координат
радиуса 3.
Определение
параметрически заданной функции.
Таким
образом, если
задают
окружность с центром в начале координат
радиуса 3.
Определение
параметрически заданной функции.
Таким
образом, если  определены
при
определены
при  и
существует обратная
функция
и
существует обратная
функция  для
для  ,
то говорят о параметрическом задании
функции
,
то говорят о параметрическом задании
функции 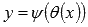 .
При
исследовании параметрически заданной
функции иногда приходится находить ее
производную по аргументу x.
В этой статье мы выведем формулу
производной параметрически заданной
функции
.
При
исследовании параметрически заданной
функции иногда приходится находить ее
производную по аргументу x.
В этой статье мы выведем формулу
производной параметрически заданной
функции 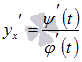 ,
также остановимся на производной второго
и n-ого порядка.
Вывод
формулы производной параметрически
заданной функции.
Пусть
определены
и дифференцируемы при
,
причем
,
также остановимся на производной второго
и n-ого порядка.
Вывод
формулы производной параметрически
заданной функции.
Пусть
определены
и дифференцируемы при
,
причем  и
имеет
обратную функцию
.
Сначала
переходим от параметрического задания
к явному. При этом получаем сложную
функцию
и
имеет
обратную функцию
.
Сначала
переходим от параметрического задания
к явному. При этом получаем сложную
функцию  ,
аргументом которой является x.
По правилу
нахождения производной сложной
функции имеем:
,
аргументом которой является x.
По правилу
нахождения производной сложной
функции имеем:  .
Так как
и
обратные
функции, то по формуле
производной обратной функции
.
Так как
и
обратные
функции, то по формуле
производной обратной функции 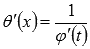 ,
поэтому
,
поэтому 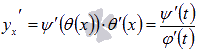 .
Давайте
рассмотрим несколько примеров.
Дальнейшее
изложение предполагает умение
пользоваться таблицей
производных, правилами
дифференцирования и
формулой производной сложной функции.
.
Давайте
рассмотрим несколько примеров.
Дальнейшее
изложение предполагает умение
пользоваться таблицей
производных, правилами
дифференцирования и
формулой производной сложной функции.



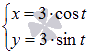 при
при 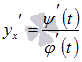 ,
также остановимся на производной второго
и n-ого порядка.
Вывод
формулы производной параметрически
заданной функции.
Пусть
определены
и дифференцируемы при
,
причем
,
также остановимся на производной второго
и n-ого порядка.
Вывод
формулы производной параметрически
заданной функции.
Пусть
определены
и дифференцируемы при
,
причем 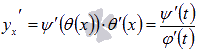 .
Давайте
рассмотрим несколько примеров.
Дальнейшее
изложение предполагает умение
пользоваться таблицей
производных, правилами
дифференцирования и
формулой производной сложной функции.
.
Давайте
рассмотрим несколько примеров.
Дальнейшее
изложение предполагает умение
пользоваться таблицей
производных, правилами
дифференцирования и
формулой производной сложной функции.