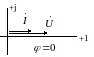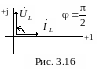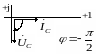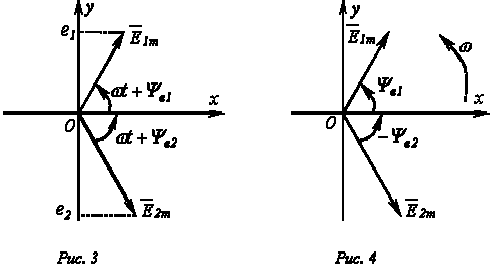- •11. Синусоидальный ток и основные характеризующие его величины.
- •Векторное изображение синусоидальных величин.
- •13.Пассивные элементы r, l, c в цепи синусоидального тока
- •1) Резистивный элемент
- •2) Индуктивный элемент
- •3) Емкостной элемент
- •14. Основы символического метода расчета цепей синусоидального тока
- •15. Комплексное сопротивление и проводимость
- •16.Треугольник сопротивлений
- •17.Закон Ома и Киргофа в символической форме записи.
- •18.Векторные диаграммы.
- •19.Активная,реактивная и полная мощность.
- •20.Ачх и фчх линейных цепей.
16.Треугольник сопротивлений
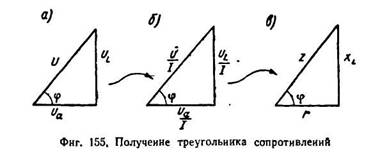
Если стороны треугольника напряжений (фиг. 155, а) разделить на ток I (фиг. 155, б), то углы треугольника от этого не из менятся, и мы получим новый треугольник, подобный первому — треугольник сопротивлений (фиг. 155, в).
|
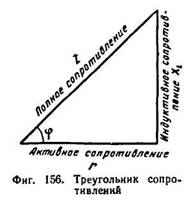
В треугольнике сопротивления, показанном отдельно на фиг. 156, все стороны обозначают сопротивления, причем гипотенуза его является полным или кажущимся сопротивлением цепи.
|
Применяя теорему Пифагора к треугольнику сопротивлений, получаем:
|
Если одно из сопротивлений цепи - (активное или реактивное), например, в 10 и более раз меньше другого, то меньшим можно пренебречь, в чем легко убедиться непосредственным расчетом.
Пример 8. Определить полное сопротивление цепи, в которой r — 9 ом и х L — 12 ом.
![]()
Было бы совершенно неправильно, если бы для определения полного сопротивления были арифметически сложены оба сопротивления r и х L, так как
9+12=21 ом.
Результат, как видим, в этом случае получается неверный.
17.Закон Ома и Киргофа в символической форме записи.
По I закону Кирхгофа алгебраическая сумма мгновенных значений токов, сходящихся в любом узле электрической цепи, равна нулю, т.е.
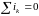 .
.
В соответствии с теоремой о сумме I закон Кирхгофа в символической или комплексной форме записывается в виде
 (3.31)
(3.31)
По II закону Кирхгофа алгебраическая сумма мгновенных значений падений напряжений в замкнутом контуре равна нулю, т.е.
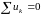 или
или
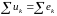 или
или
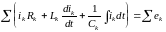 .
(3.32)
.
(3.32)
Но в соответствии с теоремами символического метода II закон Кирхгофа в символической или комплексной форме записи имеет следующий вид:
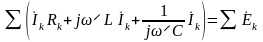 или
или
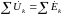 . (3.33)
. (3.33)
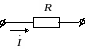
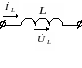
Рассмотрим закон Ома в символической форме записи для элементов цепи гармонического тока (рис. 3.15).
Рис.
3.15
|
|
|
Если
|
Закон Ома:
|
Закон
Ома:
|
На рис. 3.16 приведены векторные диаграммы напряжений и токов соответственно для сопротивления, индуктивности и емкости.
|
|
|
18.Векторные диаграммы.
Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.
|
Пусть,
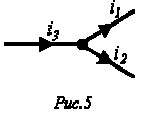
например, в точке разветвления цепи
(рис. 5) общий ток
![]() равен
сумме токов
равен
сумме токов
![]() и
и
![]() двух
ветвей:
двух
ветвей:
![]() .
.
Каждый из этих токов синусоидален и может быть представлен уравнением
![]() и
и![]() .
.
Результирующий ток также будет синусоидален:
![]() .
.
Определение
амплитуды![]() и начальной фазы
и начальной фазы
![]() этого
тока путем соответствующих тригонометрических
преобразований получается довольно
громоздким и мало наглядным, особенно,
если суммируется большое число
синусоидальных величин. Значительно
проще это осуществляется с помощью
векторной диаграммы.
этого
тока путем соответствующих тригонометрических
преобразований получается довольно
громоздким и мало наглядным, особенно,
если суммируется большое число
синусоидальных величин. Значительно
проще это осуществляется с помощью
векторной диаграммы. 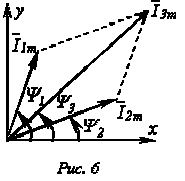 На
рис. 6 изображены начальные положения
векторов токов, проекции которых на ось
ординат дают мгновенные значения токов
для t=0.
При вращении этих
векторов с одинаковой угловой скоростью
w их
взаимное расположение не меняется, и
угол сдвига фаз между ними остается
равным
На
рис. 6 изображены начальные положения
векторов токов, проекции которых на ось
ординат дают мгновенные значения токов
для t=0.
При вращении этих
векторов с одинаковой угловой скоростью
w их
взаимное расположение не меняется, и
угол сдвига фаз между ними остается
равным
![]() .
.
Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:
![]() .
.
Построение
векторной диаграммы в масштабе позволяет
определить значения
и
из
диаграммы, после чего может быть записано
решение для мгновенного значения
путем
формального учета угловой частоты:
![]() .
.
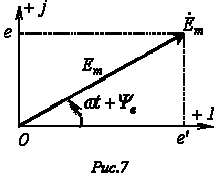

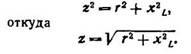

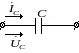
 ,
,
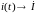 (по теореме о линейном преобразовании),
то
(по теореме о линейном преобразовании),
то
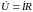 .
Это закон Ома в символической форме.
.
Это закон Ома в символической форме.

 (по
теореме о производной)
(по
теореме о производной)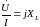 .
.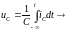
 (по теореме об
интеграле)
(по теореме об
интеграле)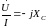 .
.