Криволинейный интеграл

где точка означает скалярное произведение,   — векторный элемент криволинейного пути, вдоль которого происходит интегрирование,   — проекция   на (положительную) касательную к криволинейному пути,   — скалярный элемент пути (элемент длины), C — конкретная кривая — путь интегрирования (обычно полагаемая достаточно гладкой). Пожалуй, простейшим физическим прообразом такого интеграла является работа силы  , действующей на точку при перемещении точки по заданному пути.

Циркуляция

— интеграл по замкнутому контуру:

где подынтегральное выражение совпадает с описанным чуть выше, а отличие состоит в пути интегрирования C, который в данном случае по определению замкнут, что обозначается кружком на знаке интеграла.

Поток векторного поля

 через поверхность S определяется как интеграл по S:

,

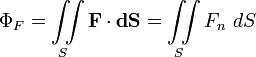где   — проекция вектора поля на нормаль к поверхности,   — «векторный элемент поверхности», определяемый, как вектор единичной нормали, умноженный на  . Простейшим примером этой конструкции является объём жидкости, проходящий через поверхность S, при её течении со скоростью F.

Производная

Аналогом производной для векторного поля выступает тензор частных производных (якобиан), который в декартовых координатах имеет вид:

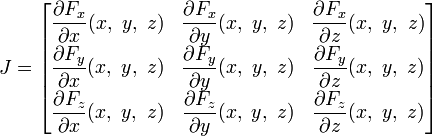
Дивергенция

— след такого тензора производных. Она не зависит от системы координат (является инвариантом преобразований координат, скаляром), а в прямоугольных декартовых координатах вычисляется по формуле:

Это же выражение можно записать с использованием символического оператора набла

Теорема Остроградского-Гаусса позволяет вычислить поток векторного поля с помощью объёмного интеграла от дивергенции поля.

Ротор

— векторная характеристика вихревой составляющей векторного поля. Это вектор с координатами:

,

где i, j и k — единичные орты для осей x, y и z соответственно.

Для удобства запоминания можно условно представлять ротор как векторное произведение:

Градиент

— важнейшая и простейшая операция, позволяющая получить векторное поле из скалярного поля. Полученное применением такой операции к скалярному полю f векторное поле называется градиентом f:

или, записывая с помощью наблы:

Векторное поле, дивергенция которого всюду равна нулю, называется соленоидальным; оно может быть представлено какротор некоторого другого векторного поля.

Векторное поле, ротор которого равен нулю в любой точке, называется потенциальным (безвихревым); оно может быть представлено как градиент некоторого скалярного поля (потенциала).

Имеет место теорема Гельмгольца: если всюду в области D у векторного поля определены дивергенция и ротор, то это поле может быть представлено в виде суммы потенциального и соленоидального поля.

Векторное поле, у которого и дивергенция, и ротор всюду равны нулю, называется гармоническим; его потенциал представляет собой гармоническую функцию.

Интегральные кривые (силовые линии)

Силовые линии магнитного поля

Интегральной кривой (также - векторной линией, для силовых полей - силовой линией, для поля скорости движения жидкости или газа - линией тока; первые термины являются общими, остальные - их синонимами в зависимости от контекста) для поля   называется кривая  , касательная к которой во всех точках кривой совпадает со значением поля:

Для силовых полей силовые линии наглядно показывают направление воздействия полевых сил.

Если в достаточно малой области пространства поле нигде не обращается в нуль, то через каждую точку этой области проходит одна и только одна силовая линия. Точки, где вектор поля нулевой — особые, в них направление поля не определено, и поведение силовых линий в окрестности этих точек может быть различным: возможно, через особую точку проходит бесконечно много силовых линий, но возможно, что не проходит ни одна. Векторное поле называется полным, если его интегральные кривые определены на всём многообразии.

Векторные поля в n-мерном пространстве

Все перечисленные для векторных полей в трёхмерном пространстве конструкции и свойства непосредственно обобщаются на любую конечную размерность пространства n.

При этом большинство таких обобщений вполне тривиальны, за исключением определения ротора, для корректного построения которого в произвольном n-мерном случае, в отличие от трёхмерного, приходится воспользоваться внешним, а не векторным (которое определено лишь для трёхмерного случая) произведением. При n=2 соответствующая операция принимает вид псевдоскалярного произведения.

Кроме того, в случае произвольного n нужна определенная аккуратность c определением потока. Основные определения оказываются полностью аналогичными для потока через гиперповерхность размерности (n — 1).

Линейные операции над векторами

Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.

Пусть а и b — два произвольных вектора. Возьмем произвольную точку О и построим вектор ОА=а. От точки А отложим вектор АВ = b . Вектор ОВ, соединяющий начало первого вектора с концом второго, называется суммой векторов а и b : О B=а+b (см. рис. 2)

.

Это правило сложения векторов называют правилом треугольника. Сумму двух векторов можно построить также по правилу параллелoграмма (см. рис. 3).

На рисунке 4 показано сложение трех векторов а, b и с.

 

Под разностью векторов а и b понимается вектор с=а-b такой, что b+с=а (см. рис. 5).

 

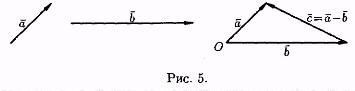
Отметим, что в параллелограмме, построенном на векторах а и b одна направленная диагональ является суммой векторов а и b , а другая — разностью (см. рис. 6).

Можно вычитать векторы по правилу: а - b = а + (-b ), т. е. вычитание векторов заменить сложением вектора а с вектором, противоположным вектору b .

Произведением вектора а на скаляр (число) λ  называется вектор λ*а (или а*λ), который имеет длину    |λ|*|а|, коллинеарен вектору а, имеет направление вектора а, если λ>0 и противоположное направление, если λ<0. Из определения произведения вектора на число следуют свойства этого произведения:

1) если b=λ * а , то b || а . Наоборот, если b ||а , (а0 ), то при некотором λ  верно равенство b = λа ;

2)    всегда а =|а | • а ^-о , т. е. каждый вектор равен произведению его мо дуля на орт.

Линейные операции над векторами обладают следующими свойствами:

1.    а+b=b+а 2.    (а +b)+с=а +(b +с), 3.    λ1 • (λ2 •а) =λ1 •λ2 •а, 4.      (λ1 +λ2) •а =λ1 •а +λ2 •а, 5.    λ • (а +b) =λ •а+λ •b.

Эти свойства позволяют проводить преобразования в линейных операциях с вектором так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать, выносить за скобки как скалярные, так и векторные общие множители.

Проекция вектора на ось

Пусть в пространстве задана ось l, т. е. направленная прямая.

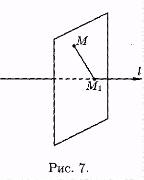
Проекцией точки М на ось l называется основание М₁ перпендикуляра ММ₁, опущенного из точки на ось.

Точка М₁ есть точка пересечения оси l с плоскостью, проходящей через точку М перпендикулярно оси (см. рис. 7).

Если точка М лежит на оси l, то проекция точки М на ось совпадает с М1.

Пусть АВ — произвольный вектор (АВ 0). Обозначим через А₁ и b ₁проекции на ось l соответственно начала А и конца В вектора АВ и рассмотрим вектор А₁В₁

Проекцией вектора АВ на ось l называет ся положительное число |A ₁B ₁ | , если вектор А ₁В ₁ и ось l одинаково направлены и отрица тельное число — |A ₁B ₁ | , если вектор А ₁В₁ и ось l противоположно направлены (см. рис. 8). Если точки a ₁и b ₁совпадают (А ₁В ₁ =0), то проекция вектора АВ равна 0.

Проекция вектора АВ на ось l обозначается так: пр_lАВ. Если АВ=0 или АВl , то пр_l АВ=0.

Угол   между вектором а и осью l (или угол между двумя векторами) изображен на рисунке 9. Очевидно,

 22. Постановка задачи. В плоском канале, ограниченном горизонтальными жесткими крышкой и дном, находятся два слоя жидкости различных по плотности, вязкости и глубине. Жидкость с меньшей плотностью располагается над более тяжелой жидкостью (стратификация устойчивая). Предполагается, что жидкости являются несжимаемыми и не перемешиваются. Обе жидкости двигаются под действием стационарного продольного градиента давления. В такой системе поперечная компонента скорости отсутствует, а вертикальный профиль горизонтальной скорости, состоит из участков парабол, т. е. имеет место двухслойное ламинарное течение Пуазейля (см, рис. 1):

,    ,    ,

,    ,        ,

где   – скорость на границе раздела,  , - вязкости,  , - толщины жидкостей соответственно. Обозначим для определенности характеристики верхней жидкости индексом 1, а нижней – 2. Таким образом, видно, что профиль горизонтальной скорости зависит только от отношений вязкостей  , и глубин   жидкостей.

 

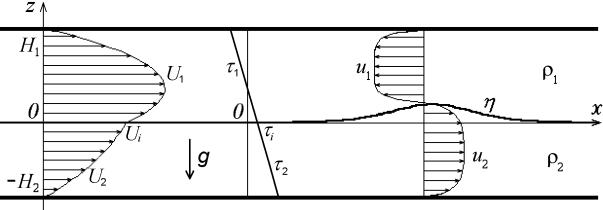
Рис. 1. Схема стационарных течения и трения, а также волнового процесса.

 

Наложим возмущение на границу раздела жидкостей, используя ряд предположений

1)           амплитуда возмущений существенно меньше глубины каждой из жидкостей  ~  (  – малый параметр);

2)           возмущения являются длинноволновыми, т. е. характерный продольный размер волны заметно больше глубин жидкостей  ~ ;

3)           толщины  вязких пограничных слоев  для возмущения  у крышки, дна и границы раздела значительно меньше глубин жидкостей  ~ .

Кроме того, будем рассматривать только такие скорости потока, при которых течение является ламинарным. При этом система уравнений Навье-Стокса заметно упрощается и приводится к следующему виду:

   (1)

   (2)

,   (3)

Здесь t – время,  - возмущения горизонтальной и вертикальной составляющих скоростей жидкостей,  - кинематические вязкости,  - плотности жидкостей, а   - возмущения давлений в слоях. Полная горизонтальная скорость, представляет сумму потоковой скорости и скорости для возмущения:   . 

Пренебрегая поверхностным натяжением, поставим обычные краевые условия на границе раздела, крышке и дне:

,    ,    ,   при     ;

,       при    ;    ,       при    ;

где    – возмущение границы раздела,   – трение жидкости, а индексом i помечены значения величин на границе раздела.

В случае волн на поверхности однородной жидкости аналогичная постановка  задачи  была  использована  в статье [10].

42. Принцип Ферма, названный так по имени сформулировавшего его французского физика и математика Пьера Ферма (является примером так называемого принципа экстремума. Принцип экстремума гласит, что любая система стремится к состоянию, при котором значение исследуемой величины принимает максимально или минимально возможное (т. н. экстремальное) значение. Вообще, принцип экстремума лежит в основе целого ряда законов геометрической оптики и распространения света. Что касается принципа Ферма, то он является простым математическим обобщением ранее сделанных наблюдений такого рода, и ранее открытые закон отражения света и закон Снеллиуса непосредственно вытекают из него. То есть, принцип Ферма можно считать теоретическим обобщением всех полученных к моменту его формулировки экспериментальных данных о поведении света.

Ферма принцип Ферма принцип. Илл. Ферма принцип, основной принцип геометрической оптики. Простейшая форма Ф. п. – утверждение, что луч света всегда распространяется в пространстве между двумя точками по тому пути, по которому время его прохождения меньше, чем по любому из всех др. путей, соединяющих эти точки. Время прохождения светом расстояния l, заполненного средой с преломления показателем n, пропорционально оптической длине пути S; S = 1•n для однородной среды, а при переменном n  . Поэтому можно сказать, что Ф. п. есть принцип наименьшей оптической длины пути. Ф. п. представляет собой вариационный принцип, утверждающий, что реальный луч света распространяется от одной точки к другой по линии, по которой время его прохождения экстремально или одинаково по сравнению с временами прохождения по всем др. линиям, соединяющим эти точки. Это означает, что оптическая длина пути луча может быть не только минимальной, но и максимальной либо равной всем остальным возможным путям, соединяющим указанные точки.