Удельная (потенциальная) энергия деформации при растяжении (сжатии). Закон Гука в развёрнутом виде.
Внешние силы в процессе деформации тела производят работу. Часть затраченной на деформацию энергии поглощается телом и накапливается в нем в виде потенциальной энергии, называемой потенциальной энергией деформации. Остальная часть расходуется на необратимые процессы - нагрев тела, изменение его электромагнитных свойств и т. д. Соотношение между этими двумя слагаемыми энергии внешних сил изменяется в процессе нагружения тела.
В пределах упругих деформаций затрата энергии на необратимые процессы весьма незначительна, и поэтому можно считать, что в пределах упругости работа внешних сил полностью переходит в потенциальную энергию деформации. Таким образом, упругое тело является как бы аккумулятором энергии.
При разгрузке идеально упругого тела накопленная в нем потенциальная энергия полностью расходуется на восстановление его первоначальной формы и размеров, причем эту работу производят внутренние силы. Следовательно, потенциальная энергия деформации равна работе внутренних сил упругости на перемещениях точек их приложения, и поэтому всегда может быть выражена через эти силы. Формула (3.44) дает возможность определить удельную потенциальную энергию деформации в общем случае объемного напряженного состояния. В частном случае линейного растяжения, имеем:
. (4.14)
Потенциальная энергия деформации U определится из уравнения (4.15) путем интегрирования по объему:
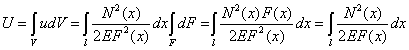. (4.15)
Например, в брусе постоянного сечения при действии постоянной по длине силы P, имеем
. (4.16)
Билет 6.
Зависимость между деформацией и перемещением при плоском и объёмном напряжённом состояниях. Обобщённый закон Гука.
Возможны два вида перемещений: перемещение всего тела как единого целого без деформирования — такие перемещения изучает теоретическая механика как перемещения абсолютно твердого тела, и перемещение, связанное с деформацией тела — такие перемещения изучает теория упругости.
Деформирование
тела вызвано разницей в перемещениях
различных его точек. Бесконечно малый
параллелепипед с ребрами
вырезанный из упругого тела около
произвольной точки z
, вследствие различных перемещений его
точек деформируется таким образом, что
изменяется длина его ребер и искажаются
первоначально прямые углы между гранями.
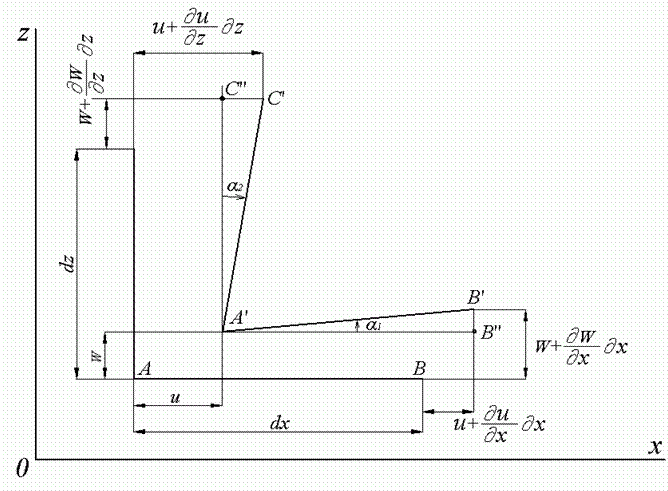
После деформации точки принимают положение При этом точка получит перемещение, составляющие которого в плоскости чертежа равны и Точка отстоящая от точки на бесконечно малом расстоянии получит перемещение, составляющие которого будут отличаться от составляющих перемещения точки на бесконечно малую величину за счет изменения координаты X
Составляющие перемещения точки будут отличаться от составляющих перемещения точки на бесконечно малую величину за счет изменения координаты φ:
Длина проекции ребра на ось после деформации:
(1.31)
Проекция абсолютного удлинения ребра на ось
Относительное удлинение вдоль оси
(1.32)
называется линейной деформацией по направлению оси .