15. Смешанное соединение, анализ и векторная диаграмма.

Смешанным соединением резисторов называется такоесоединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.

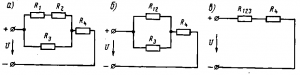Рис. 27. Схемы смешанного соединения сопротивлений

Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле

R₁₂₃=R₁₂R₃/(R₁₂+R₃)=(R₁+R₂)R₃/(R₁+R₂+R₃).

При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:

R_эк = R₁₂₃ + R₄ = (R₁ + R₂) R₃ / (R₁ + R₂ + R₃) + R₄

Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.

Векторная диаграмма — графическое изображение меняющихся по закону синуса (косинуса) величин и соотношений между ними при помощи направленных отрезков — векторов. Векторные диаграммы широко применяются в электротехнике, акустике, оптике, теории колебаний и т д.

Векторные диаграммы можно считать вариантом (и иллюстрацией) представления колебаний в виде комплексных чисел. При таком сопоставлении ось Ox соответствует оси действительных чисел, а ось Oy - оси чисто мнимых чисел (положительный единичный вектор вдоль которой есть мнимая единица).

Тогда вектор длиной A, вращающийся в комплексной плоскости с постоянной угловой скоростью ω с начальным углом φ₀ запишется как комплексное число

а его действительная часть

-есть гармоническое колебание с циклической частотой ω и начальной фазой φ₀.

Хотя, как видно уже из вышесказанного, векторные диаграммы и комплексное представление колебаний теснейшим образом связаны и по сути представляют собой варианты или разные стороны одного и того же метода, они, тем не менее, обладают своими особенностями и могут применяться и по отдельности.

• Метод векторных диаграмм может излагаться отдельно в курсах электротехники или элементарной физики, если по тем или иным причинам (обычно связанным с умеренным уровнем математической подготовки учащихся и недостатком времени) надо избежать использования комплексных чисел (в явном виде) вообще.

• Метод комплексного представления (который при необходимости или желании может включать и графическое представление, что, правда, совершенно не обязательно и иногда излишне) вообще говоря более мощен, т.к. естественно включает в себя, например, составление и решение систем уравнений любой сложности, в то время как метод векторных диаграмм в чистом виде всё же ограничен задачами, подразумевающим суммирование, которое можно изобразить на одном чертеже.

• Однако метод векторных диаграмм (в чистом виде или в качестве графической составляющей метода комплексного представления) - более нагляден, а значит в некоторых случаях потенциально более надежен (позволяет до некоторой степени избежать грубых случайных ошибок, которые могут встречаться при абстрактных алгебраических вычислениях) и позволяет в некоторых случаях достичь в каком-то смысле более глубокого понимания задачи.

16) Активная, реактивная и полная мощности. Баланс активных реактивных мощностей. Треугольник мощностей.

Электрическая мощность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.

Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком- либо участке электрической цепи. (p=u*i)

Мощность постоянного тока

Так как значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, то мощность можно вычислить по формулам:

Для того чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности, удобно обратиться к теории комплексных чисел. Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол  (сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения.

Активная мощность (P)

Единица измерения — ватт (W, Вт).

Активной мощностью называется мощность, затраченная на выполнение полезной работы.

Среднее за период Т значение мгновенной мощности называется

активной мощностью:

В цепях однофазного синусоидального тока , где U и I — действующие значения

напряжения и тока,  — угол сдвига фаз между ними.

Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле

С полной мощностью S активная связана соотношением

Реактивная мощность (Q)

Единица измерения — вольт-ампер реактивный (var, вар)

Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению действующих значений напряжения U и тока I, умноженному на синус угла сдвига фаз  между ними: (если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным).

Физически "реактивная мощность" - это, например, энергия, затрачиваемая на перемагничивание короткозамкнутой обмотки асинхронного двигателя при его работе, то есть ЛЮБОЙ асинхронный двигатель потребляет реактивную мощность из сети независимо от момента на своем валу. Реактивная мощность связана с полной мощностью S и активной мощностью Р соотношением:

В соответствии с формулой реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Необходимо отметить, что величина sin ф для значений ф от 0 до плюс 90° является положительной величиной. Величина sin ф для значений ф от 0 до —90° является отрицательной величиной. Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Отрицательное значение активной мощности нагрузки характеризовало бы нагрузку как генератор энергии. Активное, индуктивное, ёмкостное сопротивление не могут быть источниками постоянной энергии.

Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения.

Полная мощность (S)

Единица полной электрической мощности — вольт-ампер (V*A, В*А)

Полная мощность — величина, равная произведению действующих значений периодического электрического тока I в цепи и напряжения U на её зажимах: ; связана с активной и реактивной мощностями соотношением: , где P— активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q > 0, а при ёмкостной Q < 0).

Уравнение баланса активных реактивных мощностей