
- •В.4 Матрицы и операции над ними
- •В.5 ,6 Определители, их свойства и вычисление
- •Решение произвольных линейных систем
- •В 11. Векторы в пространстве: линейные операции над векторами в геометрической форме,проекция вектора на ось
- •Свойства непрерывных функций
- •. Правило Лопиталя. Формула Тейлора
- •План исследования функции и построения графика
В.4 Матрицы и операции над ними
Матрицей
называется
прямоугольная таблица, составленная
из элементов некоторого множества.
Горизонтальные ряды такой таблицы
называются строками
матрицы, а вертикальные – ее столбцами.
Матрицы обозначают A,
B,
C,
X
… . Запись
aij
используется
для указания местоположения
элемента матрицы
(i
– номер строки, j
– номер столбца). Числовую матрицу
размера
![]() (то есть состоящую из m
строк и n
столбцов чисел) в общем случае записывают
в виде:
(то есть состоящую из m
строк и n
столбцов чисел) в общем случае записывают
в виде:
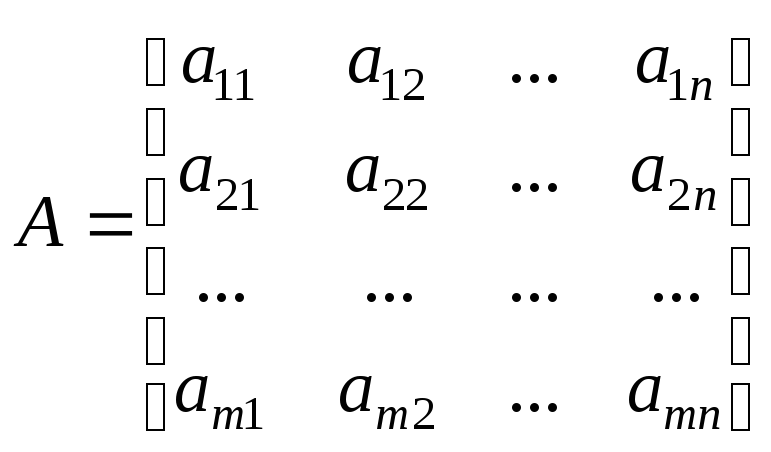
или в более компактной
форме
![]() ,
,
![]() .
.
Eё
обозначают также
![]() .
.
Если
![]() ,
то матрицу называют квадратной
и обычно обозначают An.
Элементы aii,
(
,
то матрицу называют квадратной
и обычно обозначают An.
Элементы aii,
(![]() )
такой матрицы образуют ее главную
диагональ.
)
такой матрицы образуют ее главную
диагональ.
Квадратная матрица
вида
 ,
(1)
,
(1)
где
![]()
![]() ,
называется диагональной.
Если
,
называется диагональной.
Если
![]() для любого
для любого
![]() ,
то матрица (1) называется единичной
и обозначается En.
,
то матрица (1) называется единичной
и обозначается En.
Верхней и нижней треугольной матрицами называются квадратные матрицы вида
 и
и

соответственно.
Трапециевидной матрицей называется матрица вида
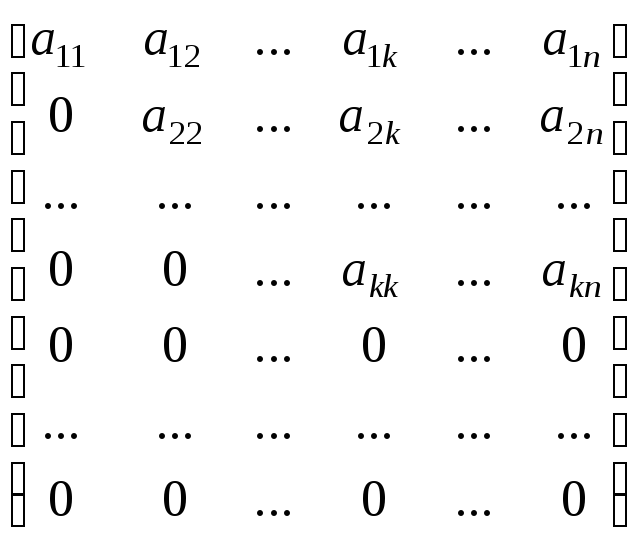 ,
,
где числа a11, a12, …, akk отличны от нуля.
Нулевой матрицей называется матрица, все элементы которой равны нулю. Обозначают такую матрицу буквой O.
Две матрицы одинакового размера
![]() и
и
![]() (2)
(2)
называются равными,
если
![]() для всех
для всех
![]() .
.
Суммой матриц
(2) называется матрица A+B
размера m×n,
состоящая из элементов
![]() ,
где
,
где
![]() .
.
Произведением
матрицы
Am×n
на число α называется матрица
![]() .
.
Разностью матриц (2) называется матрица A–B = A+ (–1)B.
Свойства операций сложения матриц и умножения на число:
-
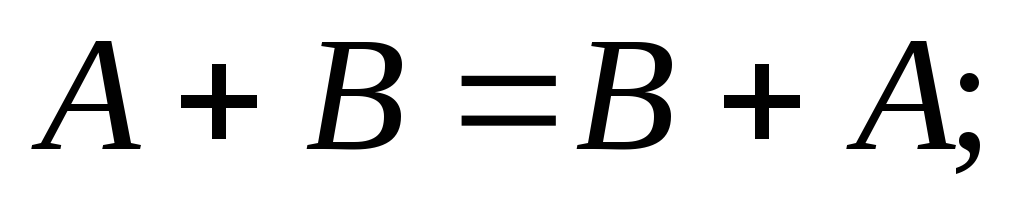
-

-
0·A=О;
-

-

-
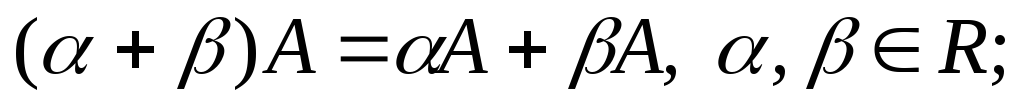
-
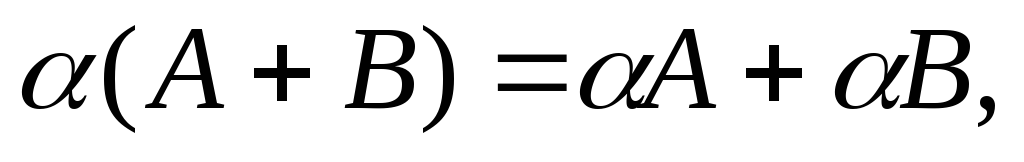
 A
и B
– матрицы одинакового размера.
A
и B
– матрицы одинакового размера.
Для матриц A и B может быть введена операция умножения A·B при условии, что матрицы согласованы, т. е. количество столбцов матрицы A равно количеству строк матрицы B.
Произведением
матрицы Al×m
на матрицу Bm×n
называется матрица
![]() элементы которой
элементы которой
![]() .
.
Для
получения элемента
![]() матрицы – произведения умножают
последовательно каждый элемент
матрицы – произведения умножают
последовательно каждый элемент
![]() строки
матрицы А
на
каждый элемент j-го
столбца матрицы
В и
находят сумму этих произведений.
строки
матрицы А
на
каждый элемент j-го
столбца матрицы
В и
находят сумму этих произведений.
Свойства операции умножения матриц:
В общем случае из
существования AB
не следует существование BA.
Даже если оба эти произведения определены,
они не всегда равны. Матрицы, для которых
![]() называются коммутативными.
называются коммутативными.
Пусть A
– квадратная матрица. Тогда k-я
степень (![]() )
матрицы A
определяется равенством
)
матрицы A
определяется равенством
![]() .
По определению принимают
.
По определению принимают
![]() при условии
при условии
![]()
Матрица AT
, полученная из матрицы A
заменой столбцов строками с теми же
номерами, называется транспонированной
к матрице A,
то есть
![]()
Свойства операции транспонирования матриц:
Если для квадратной
матрицы A
выполняется соотношение
![]() то матрица A
называется симметрической
матрицей, а если
то матрица A
называется симметрической
матрицей, а если
![]() – то кососимметрической.
– то кососимметрической.
Элементарными преобразованиями над строками матрицы A называют следующие операции:
-
перестановку строк;
-
умножение строки на ненулевое число;
-
прибавление к элементам строки соответствующих элементов другой строки, умноженных на ненулевое число.
Говорят, что матрица A эквивалентна матрице B (пишут: A~B), если матрица B получена из A при помощи элементарных преобразований строк.
