1.14. Дати означення незалежності і залежності двох подій, попарної незалежності декількох подій, незалежності у сукупності декількох подій, умовної імовірності події .Навести приклади.

Подія B – незалежна від події А, якщо поява події А не змінює імовірності події В, тобто якщо умовна імовірність події В дорівнює його безумовної ймовірності:

PA(B) = P(B). Так само PB(A) = P(A). Дві події наз-ся незалежними, якщо імовірність їх суміщення дорівнює добутку ймовірностей цих подій, в іншому разі події називають залежними.

Декілька подій наз-ють попарно незалежними, якщо кожні дві з них незалежні.

Декілька подій називають незалежними в сукупності (або просто незалежними), якщо незалежні кожні дві із них і незалежна кожна подія і всі можливі добутки інших.

Умовною імовірністю PA(B) називають імовірність події В, обчислену за умови, що подія А уже наступила.

1.15. Виписати формулу для обчислення імовірності хоча б однієї з декількох подій, незалежних у сукупності.Пояснити зміст позначень. Навести приклади.

Події називаються незалежними якщо імовірність появи однієї не залежить від появи або не появи іншої. P=a/n-імовірність певної події,а-кількісь наслідків єксперименту, коли відбвається певна подія. N-загальна кількість наслідків експерименту.Тож імовірність появи хоча б одієї події буде Р=Р1+Р2...+Рn,де Р1,Р2, Рn імовірності появи незалежних подій. Приклад:кидання двох монет, поява орла чи решки внаслідок киданя однієї монети не залежить від результату кидання другої монети. Потрібно додати що якщо події незалежні то умовна імовірність події дорівнює її безумовнії імовірності.

1.16. Вивести формули: а) повної імовірності; б) Байеса. Пояснити зміст позначень. Навести приклади застосування цих формул.

Імовірність події А, яка може настати лише при умові появи однієї з несумісних подій В1,В2,В3..В_n, які утворюють повну групу, дорівнює сумі добутків імовірностей кожної з цих подій на відповідну умовну імовірність події А. P(A)=P(B1)*P_B1(A)+P(B2)*P_B2(A)+ ...P(B_n)P_Bn(A).

Це формула повної імовірності. P(A)-імовірність події А, P(B1)-імовірність події В1, P_B1(A)-умовна імовірність події А при виконанні події В1.

Приклад: В першій коробці 20 радіоламп, з них 18 стандартних, в другій – 10 ламп, з них 9 стандартних. З другої коробки навмання взята лампа і перекладена в першу.

Формула Байєса:

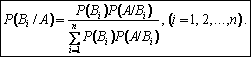
P_A(B1)=(P(Bi)*P_Bi(A))/(P(B1)*P_B1(A)+P(B2)*P_B2(A)+…+P(Bn)*P_Bn(A)).Пояснення букв як і для повної імовірності. Формули Байєса дозволяють переоцінити імовірність гіпотез, після того, як стає відомим результат випробовування, в результаті якого з’явилася подія А.

Приклад: Деталі потрапляють на перевірку до одного з двох контролерів. Імовірність, що попаде до першого-0,6, що до другого-0,4. Імовірність того що деталь буде признана стандартною першим контролером-0,95. Другим-0,93. Деталь була признана стандартною. Яка імовірність того, що деталь перевірив перший контролер?

1.17. Описати схему випробувань Бернулі. Записати формулу Бернулі.Навести приклади її застосування.

Незалежні випробування. Нехай проводяться n випробувань, у кожному з яких подія А може відбутись або не відбутись. Якщо ця ймовірність у кожному випробуванні не залежить від того, відбулась вона в інших випробуваннях чи ні, то такі випробування називаються незалежними щодо події А. Згідно з означенням випробування також незалежні, якщо в кожному з них імовірність настання події А однакова. Імовірність того, що подія А відбудеться в кожному з незалежних випробувань, позначають а ймовірність настання протилежної події Для розв’язування задач на повторні незалежні випробування застосовують такі формули і теореми.Формула Бернуллі. Імовірність того, що в n незалежних випробуваннях, у кожному з яких імовірність Р(А) = р, подія А відбудеться m раз, подається так: