50. Решением какого уравнения являются солитоны?

Уравнения Кортевега-де Фриза

51. В чем состоит принцип сведения краевых задач к вариационным задачам (принцип Дирихле)?

Метод сведения краевых задач для уравнения Лапласа к эквивалентным им вариационным задачам носит название принципа Дирихле

Поиск решения уравнения

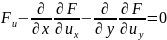
Равносилен отысканию функции, реализующей минимум функционала

52. Как ставится вариационная задача на собственные значения?

Допустимой функцией называется функция, непрерывная в 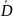, кусочно-непрерывно дифференцируемая в , принимающая заданное непрерывное значение 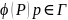на кривой Г изнутри D, и интеграл Дирихле

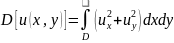
От которой он конечен

Задача на собственные значения:

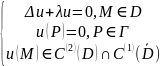
Вариационная задача: среди допустимых функций, таких, что 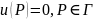, найти ту, для которой функционал :

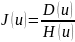
Принимает наименьшее значение

Если 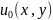реализует минимум функционала J(u) и 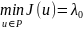(где P – класс допустимых функций), то – решение задачи на собственные значения и среди всех собственных значений этой задачи 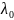– минимальное.

53. Что такое вариационные и что такое проекционные алгоритмы?

Вариационные алгоритмы – суть состоит в замене исходной краевой задачи равносильной вариационной задачей. Пример – принцип Дирихле

Проекционные алгоритмы – суть состоит в замене исходной задачи задачей нахождения коэффициентов разложения по некоторой системе базисных функций. Примет – метод Ритца.

54. В чем состоит метод Ритца?

Пусть дано уравнени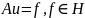е , где

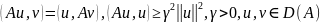
1) Выбирается базис

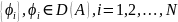
2) Приближенное решение ищется в виде

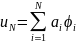
3) Коэффициенты 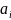находятся из системы уравнений

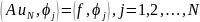
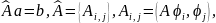
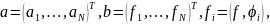
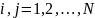
Если для любой функции можно построить такую последовательность элементов

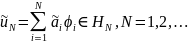
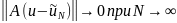
то приближенные решения 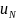сходятся к точному решению уравнения 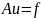(см. усл. выше) пр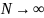и и

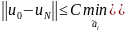
Основной недостаток метода Ритца состоит в том, что он применим только для самосопряженных положительно определенных операторов.

55. Что такое энергетическое пространство? В каком случае его можно построить?

Пусть А – линейный оператор в Гильбертовом пространстве, D(A) – область его определения.

Введем в D(A) энергетическое скалярное произведение и норму:

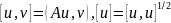
И дополним D(A) по энергетической норме. Получим энергетическое пространство 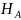, порождаемое оператором A. Оператор А должен быть положительно определен и симметричен (а значит и линеен).

56. Какие краевые условия называются главными, и какие естественными?

Краевые условия, которым удовлетворяют элементы из D(A), называются естественными для оператора А, а краевые условия, которым удовлетворяют как элементы из D(A), так и элементы из , называются главными. Базисные функции выбираются из

57. В каких случаях метод Ритца неприменим?

Метод Ритца неприменим для операторов, которые не являются самосопряженными и положительно определенными.

58. В чем состоит метод Галеркина?

Рассмотрим задачу: 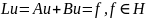, где А и В – линейные операторы в гильбертовом пространстве, причем D(A) плотно в ℋ

1) Выбираем базис

2) Приближенное решение ищется в виде

3) Коэффициенты находятся из условия ортогональности невязки 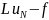к

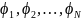
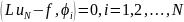
Если коэффициенты определяются из условия 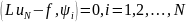, где 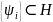, некоторый базис, то метод называется методом Галёркина-Петрова.

59. В чем состоит обобщенный метод моментов?

Рассмотрим задачу: , где 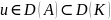и оператор А является К-положительно определенным, т.е.

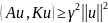
1) Выбираем базис

2) Приближенное решение ищется в виде

3) Коэффициенты находятся из системы уравнений:

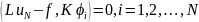
60. В чем состоит метод наименьших квадратов?

Рассмотрим задачу , где у оператора А существует ограниченный обратный оператор

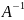
1) Выбираем базис

2) Приближенное решение ищется в виде

3) Коэффициенты находятся из системы уравнений:

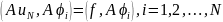
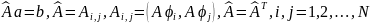
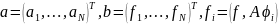
61. Дайте определение разностной схемы

Рассмотрим задачу

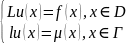
Где L – линейный дифференциальный оператор, l – оператор дополнительных (начальных, граничных) условий, 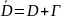, заменяем на 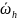- дискретное множество узлов – сетка, 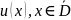заменяем на 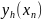– сеточные функции (зависят от параметра h),

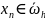
- разностные операторы

Первоначальной задаче ставится в соответствие система алгебраических (разностных) уравнений.

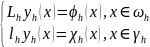
Семейство уравнений, зависящих от параметра h, называется разностной схемой.