4. Кольцевой механизм, открытый Зинером в 1950году:

Этот механизм объяснил явление самодиффузии. Он не связан с наличием дефектов. Зинер предположил, что диффузия происходит путем одновременного поворота нескольких атомов. Этот метод получил название кольцевого.

Коэффициент диффузии и величины его определяющие.

В качестве примера рассмотрим диффузию в ГЦК решетке по вакансионному механизму.

Рассмотрим диффузию в направлении оси х. Пусть в плоскости 1 находится n₁ атомов. А в плоскости 2 – n₂ атомов, но .

Г₁ – число переходов в единицу времени атомов с плоскости 1 на плоскость 2.

Г₂ – число переходов в единицу времени атомов с плоскости 2 на плоскость 1.

Г₁ ,

где ₁ – частота колебаний атомов n₁ в направлении оси х; р₁ – число мест, на которые может перейти диффундирующий атом.

Для данной решетки р₁=4, но р₁ нужно умножить на вероятность того, что места являются свободными. Кроме того, частота колебаний должна быть помножена на вероятность того, что это колебание приведет к перескоку:

где ₁ – вероятность того, что частота приведет к перескоку; ₁ – вероятность наличия свободных мест.

.

Если рассматривать диффузию собственных атомов в свободной решетке, то тогда ₁=₂, р₁=р₂, ₁=₂ и ₁=₂. Тогда результирующий поток, при условии n₁>n₂:

Перейдем от числа атомов к концентрациям. Поскольку кристалл имеет анизотропию, то в качестве концентраций надо брать погонную концентрацию (не на единицу объема, а на единицу длины):

Поскольку межатомные расстояния маленькие, то можно считать, что концентрация является квазинепрерывной функцией координаты, поэтому ее можно разложить в ряд Тейлора:

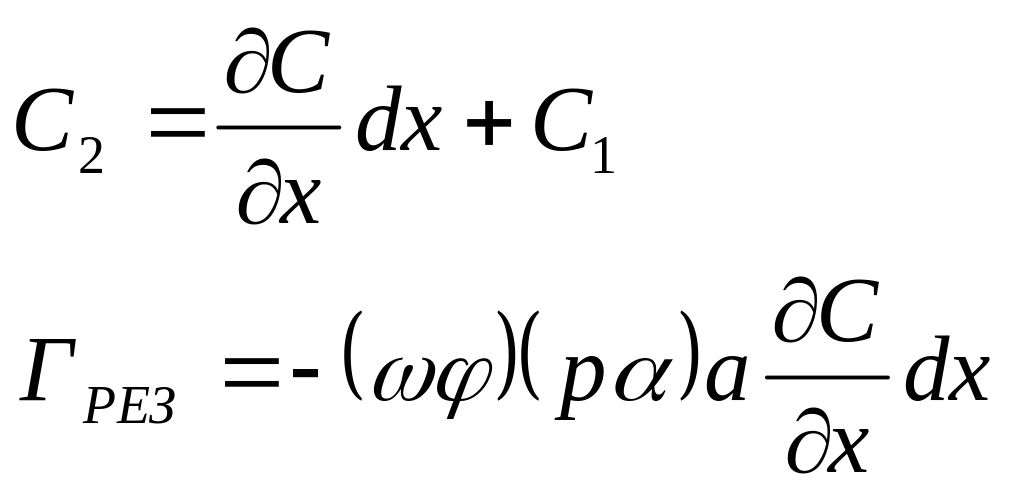
Если dxа, тогда:

.

Коэффициент диффузии зависит от направления, т.к. в его выражение входит постоянная решетки а. Чтобы его посчитать, надо знать величины, входящие в выражение.

Величина р зависит от вида решетки. Величина  - мольная доля вакансий (константа Шоттки, или константа Френкеля, т.е. или ). Для оценки частотного фактора (), надо рассматривать как диффундирующий атом движется. Для перехода на новое место атому нужно преодолеть потенциальный барьер. Изменения энергии этого атома по координате выглядит т.о.:

т.1 – исходное положение

т.2 – конечное положение

т.3 – перевальная точка.

Процесс перехода можно условно записать как мономолекулярную обратимую реакцию:

где N – концентрация атомов в т.1; n – концентрация атомов в т.2.

Работа этого процесса:

(на моль пересчет)

где К_Р – и есть вероятность преодоления потенциального барьера.

Пусть v – средняя скорость атомов в направлении оси х:

 – эффективная толщина барьера: []=м.

Тогда

(на частицу пересчет)

В направлении оси х частицы перескакивали бы с такой частотой ( ), но реально их меньше. Тогда:

Если собственный атом в собственной решетке, то m(кристалла)=1/2m(атома) – приведенная масса.

В справочниках приводят выражение для коэффициента диффузии:

где Е – энергия активации диффузии, ; D₀ – предэкспонента.

В справочниках полагают, что D₀=const в определенных температурных интервалах. Но на самом деле, она от температуры зависит слабо. Если диффузия не по вакансиям, то энергия образования вакансий =0.

Коэффициенты диффузии при нормальных условиях: 10^–8–10^–10 см²/с.