Диффузионные процессы

Связь диффузионного потока вещества с градиентом химического потенциала. Виды диффузии. Термодинамические аспекты диффузии.

Термодинамика изучает свойство систем, находящихся в состоянии равновесия.

Состояние равновесия характеризуется тем, что в системе отсутствуют направленные потока чего-либо (вещества или энергии), т.е. отсутствует перенос.

Термодинамически условию равновесия (при Р, Т=const) отвечает постоянство изобарно-изотермического, а значит и химических потенциалов во всех частях системы. Внешнее воздействие может вывести систему из состояния равновесия. Это означает, что в разных частях системы значения химического потенциала будут разными, т.е. появится градиент химического потенциала.

Существуют ситуации, когда система в целом неравновесна, но в каждой ее точке равновесие успевает установиться со своими значениями, такие равновесия называются ЛТР (локальное термодинамическое равновесие). Если убрать внешнее воздействие, то система должна снова вернуться к равновесию. Этот переход, который называют релаксацией, должен сопровождаться потоками, которые выравнивают химические потенциалы по всей системе. Очевидно, что величина потока должна определяться степенью отклонения системы от состояния равновесия, а характер потока должен определяться причиной, вызвавшей нарушение равновесия.

Рассмотрим систему в состоянии ЛТР. Пусть и - значения химического потенциала в т.1 и т.2. Изменения изобарно-изотермического потенциала, т.е. работа, при переходе от т.1 к т.2:

.

Если _I – непрерывная функция т т.1 и т.2 близко друг к другу расположены, тогда мы можем написать:

.

Тогда

Появление градиента химического потенциала приводит к возникновению некой эффективной силы, действующей на этот компонент

– на моль.

– на частицу.

Наличие силы всегда вызывает поток в направлении действия этой силы. Плотность потока:

где N_i – концентрация соответствующего компонента; v_i – скорость дрейфа.

где u_i – подвижность.

Тогда

Плотность потока вещества определяется градиентом всех параметров, описывающих состояние системы. Поток, обусловленный градиентом давления, называется бародиффузионным – .

– термодиффузионным.

– электрический ток.

Концентрационная диффузия. Коэффициент диффузии и соотношение Эйнштейна.

Под диффузией в узком смысле слова принято называть поток вещества, обусловленный градиентом концентрации. В любой системе под действием одного сорта возмущения всегда возникают потока всех видов.

Рассмотрим диффузию в узком смысле:

.

Для нашего случая:

Поскольку , где  - коэффициент активности, то

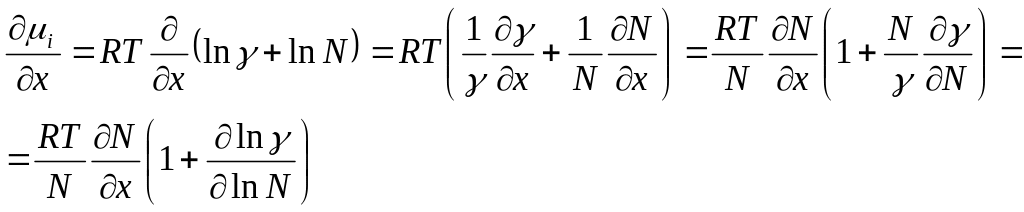
Тогда

Коротко это выражение имеет вид:

– первый закон Фика.

где D – коэффициент диффузии.

.

Первый закон Фика показывает пропорциональность плотности потока диффундирующих частиц градиенту концентрации.

Отметим, что для идеального раствора _I=1, тогда имеем:

– соотношение Эйнштейна.

В общем случае необходимо учитывать пространственно-временные изменения концентрации, для этого воспользуемся уравнением непрерывности:

, где

– характеризует изменения концентраций частиц за счет потоков частиц через данный объем; - учитывает наличие источников частиц в данном объеме.

При отсутствии источников уравнение примет вид:

– скорости.

Если D не зависит от координат, т.е. , то уравнение принимает вид:

где  – оператор Лапласа.

В прямоугольной системе координат, это уравнение имеет вид:

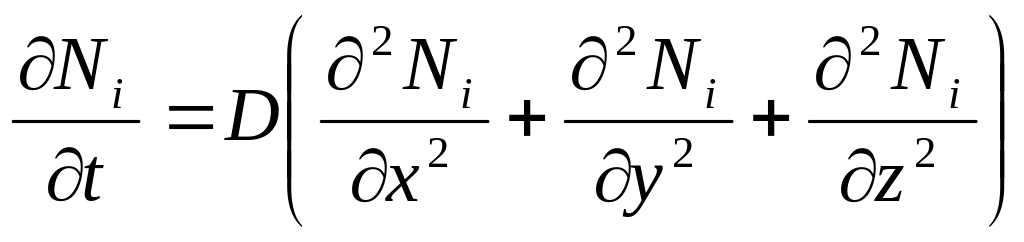- второй закон Фика.

Термодиффузия.

Термодиффузия – поток вещества, пропорциональный градиенту температуры.

Рассмотрим явление переноса вакансий и реальных частиц. Источником вакансий является тепловое движение. Появление градиента температуры должно привести к тому, что равновесная концентрация вакансий окажется неодинаковой в различных частях кристалла. Поскольку концентрация вакансий является функцией температуры, то в горячих участках концентрация выше, чем в более холодных. Следовательно, появится градиент концентрации вакансий, вектор которой совпадает с вектором градиента температуры. Т.к. концентрация вакансий обусловлена уходом из узлов реальных частиц, это значит, что формирование градиента равнозначно оттоку реальных частиц от более горячих участков к более холодным. Казалось бы, что этот отток будет продолжаться до тех пор, пока локальная концентрация вакансий не достигнет равновесной величины. Но реально этого не происходит, потому что в кристалле всегда неизбежна гибель этих вакансий. Как вакансия достигает поверхности, так она пропадает, поэтому при наличии градиента температуры, всегда происходит «разборка» более горячей плоскости и «достраивание» более холодной плоскости за счет реальных приходящих частиц. В результате осуществляется перекачка от более горячих к более холодным.

Гетеродиффузия. Эффект Киркендаля–Френкеля. Связь коэффициента гетеродиффузии с коэффициентом собственной диффузии.

Под гетеродиффузией понимают явления переноса, в которых участвуют частицы разного сорта. Это может быть перенос компонента из одной фазы в другую, это может быть перемещение частиц в одной фазе, но сложного химического состава. Рассмотрим пример: контакт двух кристаллов, один из которых состоит из атомов сорта А, другой из атомов сорта В. Предполагаем, что А и В неограниченно растворимы друг в друге. Оба кристалла имеют соответствующее равновесное количество дефектов (пусть это будут дефекты по Шоттки). В общем случае равновесные концентрации не должны быть равны друг другу:

(1)

Поэтому, если привести А и В в контакт, появится и градиент концентрации и градиент вакансий. Следовательно, появятся потоки и реальных частиц, и вакансий. Предположим, что . Это значит, что способность к дефектообразованиям у кристалла А выше, т.е. частицы А легче покидают узлы, т.е.

.

Поэтому кристалл В будет обогащаться новыми узлами, которые занимаются частицами А, поскольку А прибывает больше, чем В уходит. «Истощение» реальных частиц в кристалле А должно означать, что концентрация вакансий в нем должна расти. Конечным результатом является образование пор в кристалле А, размер которых во времени будет расти. Когда поры достигают поверхности – они исчезают. В результате кристалл А как бы сжимается, размеры его уменьшаются, а кристалл В, наоборот, увеличивает свои размеры. В результате фронт обмена частиц будет смещаться в сторону кристалла А. Явление образования пор получило название эффекта Френкелю, а изменение размера кристалла – эффекта Киркендаля.

Для этого примера плотности потоков частиц А и В складываются из двух составляющих:

1. пропорциональна градиенту концентрации;

2. связана с перемещением фронта обмена частицами:

(2)

(3)

где С_А и С_В – концентрации; v - скорость перемещения фронта обмена.

Если предположить, что количество узлов в движущейся площади обмена постоянно, это значит, что

(4)

(5)

(6)

Подставим в (6) (2) и (3), получим:

(7)

Отсюда найдем скорость перемещения фронта:

(8)

Из (8) видно, что перемещение фронта связано с различиями в коэффициентах диффузии; если коэффициенты диффузии одинаковые, то граница никуда не движется, v=0; если D_A>D_B, то v положительна – в сторону А.

Из этого следует, что коэффициенты диффузии D_A и D_B неоднозначно описывают плотности потоков компонентов, поскольку они взаимосвязаны: компонент А влияет на диффузию компонента В, и, наоборот. Найдем связь по компоненту А:

Возьмем (3) и подставим в него (8):

– уравнение Дарнега.

Отдельные коэффициенты (в нашем примере D_A и D_B) диффузии называются коэффициентами собственной диффузии или химической диффузии. Они приводятся в справочниках.

Механизм диффузии.

Известно, что атомы в кристаллах совершают колебания около положения равновесия. В определенных случаях эти колебания становятся достаточно сильными, чтобы атом мог поменять свое положение, такие перескоки и являются причиной диффузии.

Рассмотрим некоторые наиболее часто встречающиеся механизмы диффузии:

1. Междоузельный – считают, что атомы диффундируют по этому механизму, когда он переходит из 1 междоузлия в другое, не вызывая при этом непрерывного смещения атомов, находящихся в узлах решетки.

Рассмотрим как этот механизм реализуется в ГЦК решетке.

«» - междоузлия.

Из рис. видно, что междоузлия, по которым может перемещаться диффундирующий атом, сами образуют ГЦК решетку. Атом диффундирует, перескакивая из одного положения в подрешетке междоузельных точек в другое положение. Поскольку атомы в решетке удерживаются силами связи, то диффундирующий атом должен совершать работу в поле этих сил, т.е., грубо говоря, для перескока атом требуется локальная деформация решетки и процесс диффузии требует определенной энергии активации.

2. Вакансионный механизм:

Как известно, при температуре, отлично от 0 К, в кристалле всегда есть незанятые узлы, т.е. вакансии (дефекты по Шоттки и Френкелю). Если один из соседних атомов займет вакансия, то говорят, что он диффундирует по вакансионному методу. Такие перескоки тоже требуют определенных затрат энергии на работу против сил связи.

3. Диффузия по междоузлиям путем вытеснения:

Из элементарных соображений следует, что чем меньше диффундируют атомы по сравнению с атомами, расположенными в узлах решетки, тем коэффициент диффузии его будет больше. Однако экспериментальные данные показывают, что и большинство атомов могут диффундировать достаточно легко. Расчеты показывают, что в междоузельном механизме перескок таких атомов приводил бы к очень большим локальным дефектам решетки. Вероятность диффузии должна быть малой. Для объяснения этого эффекта был предложен метод диффузии путем вытеснения. Говорят, что атомы диффундируют по такому методу, если он выталкивает одного из ближайших соседей в междоузлиях, и занимая его место в решетке.