2.2.3. Уравнения вида

Уравнение не содержит . Вводим новую функцию , полагая . Тогда

.

Подставляя в уравнение выражения , получаем уравнение первого порядка относительно как функции : .

Пример 2.3.1. Решить уравнение .

▲ 1) В уравнении нет в явном виде , и оно допускает понижение порядка.

2) Положим , тогда и понизим порядок уравнения: . Получили уравнение типа I.

3) .

4) Решаем уравнение ▼

Ниже приводится сводная таблица трех типов дифференциальных уравнений второго порядка, допускающих понижение порядка, и их признаков.

Тип	Вид уравнения	Признаки	Способ понижения Порядка
А		Нет явно	Подстановка
Б	или	Явно нет	Подстановка
В	или	Явно нет	Подстановка

Определение частных решений (решение задачи Коши) для уравнений второго порядка

Пример 2.3.2. Найти частное решение .

▲ 1) Данное уравнение является уравнением типа (В).

2) Понижаем порядок подстановкой: . Получили уравнение первого порядка типа I.

3) ,

.

4) .

Общее решение .

5) Подставим начальные условия в общее решение и в результат его дифференцирования : Частное решение . ▼

Можно и находить по мере их появления.

Пример 2.3.3. Решить задачу Коши для уравнения .

▲ 1) Исходное уравнение типа (В).

2) Понижаем порядок подстановкой: ,

. Получили уравнение первого порядка типа III.

3) ;

• 

• .

• 

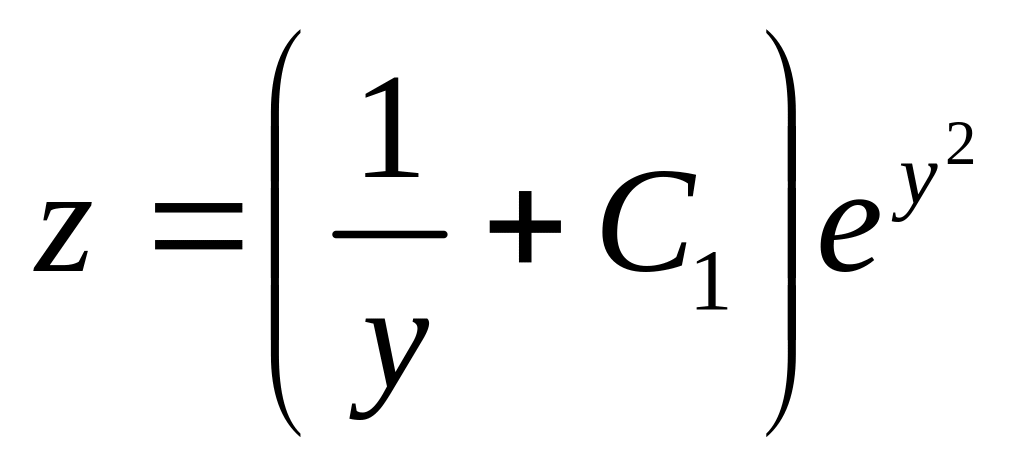
4) Найдем , воспользовавшись начальным условием

.

5) Решим уравнение при условии, что . Это уравнение типа I.

,

.

6) найдем их начальных условий. . Частное решение . ▼

2.3. Дифференциальные уравнения высших порядков,

допускающие понижение порядка

Рассмотрим уравнение вида , допускающее понижение порядка. Общее решение этого уравнения находим методом интегрирования. Умножая обе его части и интегрируя, получаем уравнение порядка:

.

Повторяя эту операцию, приходим к уравнению порядка:

.

После интегрирования получаем общее решение исходного уравнения:

,

где − произвольные постоянные, связанные определенным образом с произвольными постоянными .

Пример 3.1. Найти общее решение уравнения .

▲ Согласно правилам интегрирования имеем

,

,

,

▼

Решение задач 6-8 типового варианта

6. Найти частное решение дифференциального уравнения

и вычислить значение полученно2й функции с точностью до двух знаков после запятой.

▲ Найдем общее решение данного уравнения (уравнение типа (А)). Полагая ,

получим уравнение первого порядка типа I. Решая его, находим

.

Найдем , воспользовавшись начальным условием :

.

Решим уравнение ,

.

Найдем .

Частное решение, удовлетворяющее заданным начальным условиям, имеет вид

.

Вычислим значение функции :

. ▼

7. Найти общее решение дифференциального уравнения , допускающего понижение порядка.

▲ 1) Уравнение принадлежит к типу (В), так как нет .

2) Порядок уравнения понижается подстановкой , тогда . Подставим и в исходное уравнение: − уравнение с разделяющимися переменными (тип I).

3) ,

.

4) Заменяя , получаем уравнение с разделяющимися переменными (типа I):

, т. е. нашли общее решение исходного уравнения. ▼

8. Найти решение дифференциального уравнения , допускающего понижение порядка, которое удовлетворяет заданным условиям: .

▲ 1) Уравнение является уравнением типа (В).

2) Понижаем порядок подстановкой: . Имеем .

3) Решаем полученное уравнение типа I:

.

4) Найдем , воспользовавшись начальным условием ,

.

5) Решим уравнение . Найдем: ,

,

.

6) Найдем . Следовательно, искомое решение имеет вид

.

Геометрически оно представляет собой левую или правую половину окружности

. ▼