3.4.3. Дополнительное задание

1. Исследовать дисперсионную характеристику и сопротивление связи ЗС в «щелевой» полосе прозрачности.

2. Исследовать зависимость дисперсии ЗС от угла разворота щелей в смежных диафрагмах.

3.5. Содержание отчета

1. Цель работы, эскиз исследуемой ЗС и схема измерительной установки.

2. Краткие сведения о конструкции, характеристиках, параметрах и области применения ЗС.

3. Расчетное значение резонансной длины волны (размеры замедляющей системы, необходимые для расчета, содержатся\ в разднеле "исходные данные для предварительного задания".

4. Теоретические и экспериментальные графики распределения напряженности электрического поля в макете ЗС для всех измеренных видов колебаний, резонансные частоты этих видов и значения угла фазового сдвига, определенные с помощью сравнения теоретических и экспериментальных графиков.

5. Дисперсионные характеристики ЗС в координатах идля пространственных гармоник с номерами указанными преподавателем.

6. Расчет ускоряющего напряжения ЛБВ, использующей исследуемую ЗС на минус первой пространственной гармонике. Рабочая точка выбирается вблизи значения(точное значение указывается преподавателем). Эффективное взаимодействие достигается при условии, что скорость электронов

7. Значения сопротивления связи, рассчитанные для указанных преподавателем углов фазового сдвига и номеров пространственных гармоник (наносятся на дисперсионную характеристику около соответствующих точек).

8. Выводы и замечания по работе.

3.6. Контрольные вопросы

1. Дайте определение замедляющей системы.

2. Укажите различия между падающей и отраженной волнами, с одной стороны, и прямыми и обратными пространственными гармониками, с другой, и объясните эти отличия на примере дисперсионных характеристик

3. Могут ли модули фазовой и групповой скорости пространственной гармоники в замедляющей системе быть больше скорости света?

4. Укажите основные параметры и характеристики ЗС.

5. Как определить фазовую и групповую скорости по дисперсионной характеристике ЗС, построенной в координатах и?

6. Какие виды колебаний возможны в закороченном с обеих сторон отрезке ЗС? Приведите обоснованные примеры.

7. Какие требования предъявляются к возмущающему телу при измерении распределения поля в ЗС?

8. Какие факторы определяют погрешность измерения дисперсионной характеристики и сопротивления связи.

9. На каком явлении основан метод идентификации полей различных видов колебаний в отрезке ЗС?

4. Исследование объёмных резонаторов

Цель работы: Изучение характеристик и параметров объемных резонаторов, методов их измерений, а также исследование различных видов колебаний в цилиндрическом, коаксиальном и тороидальном объемных резонаторах. Изучение методики идентификации видов колебаний в резонаторах.

4.1. Основные теоретические положения

4.1.1. Параметры объемных резонаторов

На низких частотах в качестве колебательной системы обычно применяется контур, состоящий из сосредоточенных параметров: индуктивности , емкостии неизбежного сопротивления потерь. Такой контур, как известно из курса теоретической электротехники, характеризуется собственной частотойи добротностью.

С ростом частоты в таком контуре увеличиваются потери на излучение, а также тепловые потери вследствие сильного поверхностного эффекта в проводниках, поэтому в микроволновом диапазоне создание контуров с сосредоточенными параметрами и высокой добротностью сильно затруднено. В связи с этим в данном диапазоне применяют колебательные системы с распределенными параметрами. Они представляют собой диэлектрический объем, помещенный в другой диэлектрик или ограниченный замкнутой проводящей (металлической) оболочкой, и носят название объемных резонаторов.

К простейшим объемным резонаторам относятся короткозамкнутые отрезки металлических волноводов. В отличие от низкочастотного контура, резонатор имеет не одну, а бесконечное множество собственных частот.

Объемные резонаторы составляют неотъемлемую часть микроволновых приборов, устройств и установок – генераторов, усилителей, ускорителей заряженных частиц. Резонаторы применяются также в фильтрах, в измерительной аппаратуре (частотомеры и волномеры).

Электромагнитные колебания в резонаторе, не связанном с внешними цепями, в объеме которого отсутствуют источники поля (сторонние токи и заряды), называются собственными (или свободными).Электромагнитное поле собственных колебаний описывается системой однородных уравнений Максвелла, нетривиальные решения которых существуют при определенных значениях(и соответственно, где– скорость света), называемых собственными частотами (собственными длинами волн). Каждой частоте соответствуют определенные функции , описывающие электромагнитное поле-го вида колебаний. Вид колебаний с наименьшей собственной частотой называется основным (или низшим). Виды колебаний с более высокими собственными частотами называют высшими. Для простейших типов резонаторов различают колебания поперечного (), электрического () и магнитного () видов. Векторыэлектромагнитного поляпоперечноговида колебаний лежат в плоскости поперечного сечения резонаторов и не имеют продольных составляющих.Электрическими (магнитными) колебаниями называются колебания, у которых вектор(или) наряду с поперечными имеет и продольную составляющую(или). Следует заметить, что возможно существование колебаний гибридного-вида, у которых отличны от нуля все шесть составляющих векторови.

Электромагнитное поле резонаторов, представляющих собой закороченные отрезки волноводов, может быть описано с помощью векторов Герца (см. раздел 2.1 описания лабораторной работы 2 ):

где функция , описывающая поле в поперечном сечении, для цилиндрического резонатора имеет вид , , а для коаксиального – –. Заметим, что в отличие отбегущихволн в волноводах, в объемных резонаторах могут существовать толькостоячиеволны. Таким образом, в случае цилиндрического резонатора, возбужденного, например, на колебаниях-вида, с учетом и имеем

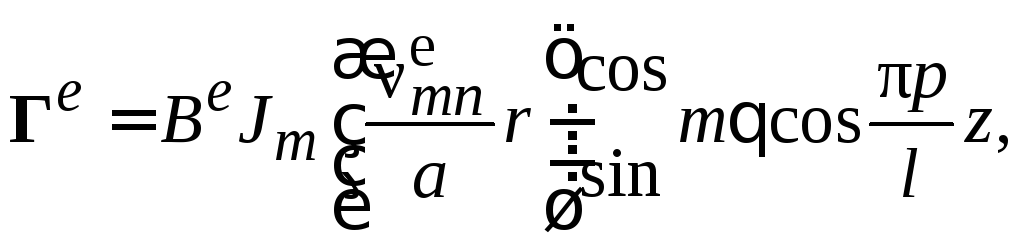
где . Скобки означают, что значениевозможно только дляE-видов колебаний.

Для -вида колебаний коаксиального резонатора с учетом и получим

где.

В приведенных выражениях – радиус оболочки,– радиус внутреннего проводника,– длина резонатора. Каждое из целых чиселопределяет число полуволн (число вариаций поля) по соответствующим координатам в пределах соответствующего геометрического размера резонатора, и, следовательно, конкретный вид колебаний. Например, для резонаторов с цилиндрической формой поверхностей – по координатам соответственноцилиндрической системы координат.

Распределение электромагнитного поля некоторых видов колебаний в простейших объемных резонаторах показано на рис. 4.1 (в цилиндрическом: а-,б - ; в коаксиальном:в– ). Заметим, что структура полей показанных видов колебаний в плоскости поперечного сечения этих резонаторов аналогична структурам полей соответствующих типов волн в плоскости поперечного сечения соответствующих волноводов:,– в круглом и – в коаксиальном.. На рисунке видно, что электромагнитные поля распределены во всем объеме резонаторов, что характеризует их как системы с распределенными параметрами. Для расчета характеристик таких резонаторов необходимо использовать весьма сложные методы теории поля (электродинамические методы). Лишь в некоторых случаях, когда у резонаторов линейные размеры много меньше собственной длины волны (квазистационарных, например, тороидальных – см. рис. 4.2), в их объеме можно выделить области преимущественной локализации (сосредоточения) электрических и магнитных полей. Для описания таких резонаторов можно использовать эквивалентные схемы, построенные на основе сосредоточенных -,- и-параметров, что позволяет использовать для расчета характеристик резонаторов приближенные и существенно более простые методы теории цепей с достаточной для практики точностью.

Объемный резонатор на каждом i-м виде колебаний характеризуют тремя основными параметрами:

– собственной частотой() или, (собственной длиной волныили), где, как уже отмечалось, индексыопределяют конкретный вид колебаний;

– собственной добротностью ;

– волновым сопротивлением , Ом.

Для резонаторов с вакуумным заполнением собственные частоты различных видов колебаний находятся по формуле

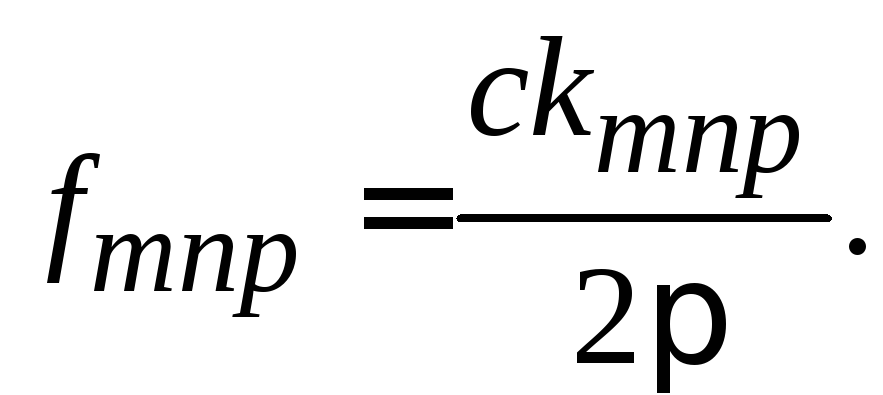
Волновое число вычисляется как квадратный корень из суммы квадратов поперечного (критического)и продольноговолновых чисел:

Значение критического волнового числа зависит от типа резонатора и вида колебания (-,- или):

– для цилиндрического резонатора

– для коаксиального резонатора

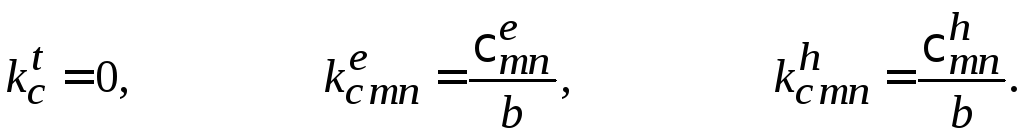
Значения корней цилиндрических функций (функций Бесселя первого и второго рода m-го порядка) для некоторых целочисленных переменныхиприведены в табл. 2.1, 2.2.

Из выражений – следует, что у полого цилиндрического резонатора при соотношении размеров среди всего множества- и-видов колебаний основным является вид, то есть при значениях индексов, и тогда формула для расчета собственной частоты принимает вид:

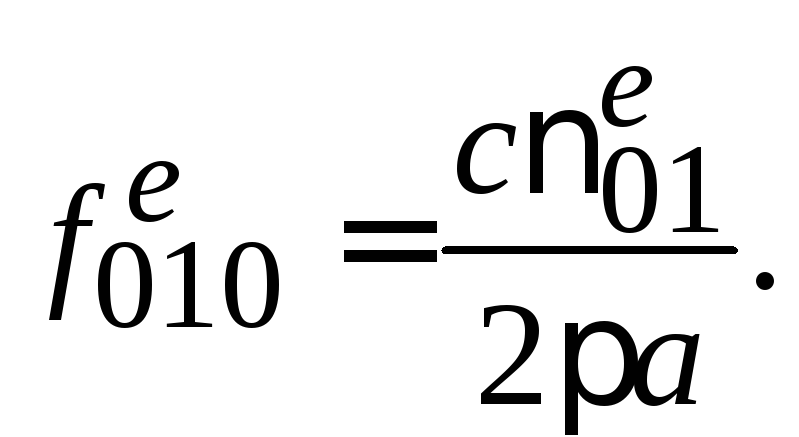
Можно показать также, что в коаксиальном резонаторе с отношением размеров наименьшей собственной частотой обладает поперечный вид колебаний:.

Из последнего соотношения следует, что и, таким образом, , т. е. на длине резонатора укладывается половина длины волны колебаний вида. Такой коаксиальный резонатор называютполуволновым.

Таким образом, собственные частоты (собственные длины волн) различных видов колебаний объемных резонаторов зависят от структуры соответствующих полей, формы резонаторов и, в общем случае, от всех его размеров.

По определению собственная добротностьрезонатора наi-м виде колебаний прямо пропорциональна отношению энергии, запасенной в электрическом и магнитном полях резонатора, к энергии, рассеиваемой в резонаторе за период колебаний:

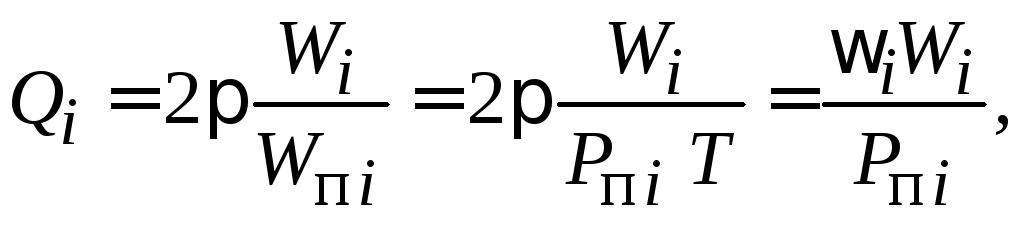
где – суммарная мощность потерь в стенках и в объеме резонатора.

Можно показать, что добротность медного цилиндрического резонатора с воздушным наполнением для вида колебаний определяется выражением

где – глубина проникновения, мм;– собственная частота, Гц;– объем резонатора,– площадь его внутренней поверхности. Глубина проникновения поля в металл в сантиметровом диапазоне длин волн составляет единицы микрометров. Если линейные размеры резонатора сравнимы с длиной волны колебаний, то собственная добротность цилиндрического резонатора для основного вида колебаний составляет величину порядка.

Волновое сопротивление определяется между двумя выбранными точкамиaиbвнутренней поверхности резонатора и его величина пропорциональна отношению квадрата модуля напряжениямежду этими точками к запасенной на данной частоте энергии электромагнитного поля

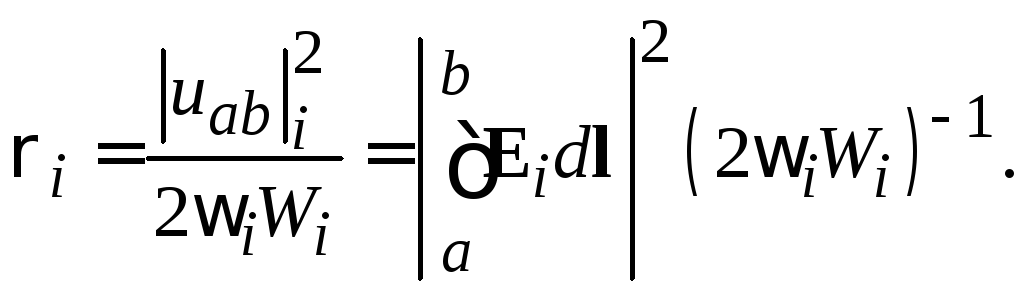
Из формулы (4.7) следует, что значение зависит от выбора точек отсчета и пути интегрирования. В резонаторах микроволновых вакуумных приборовобычно определяется вдоль траектории электронного потока, пронизывающего резонатор, и характеризует «степень концентрации» электрического поля в зазоре резонатора – в области взаимодействия электронного потока с электрическим полем. На основном виде колебанийполого цилиндрического резонатора величина, рассчитанная вдоль его оси симметрии между двумя точками на торцевых стенках, находится из в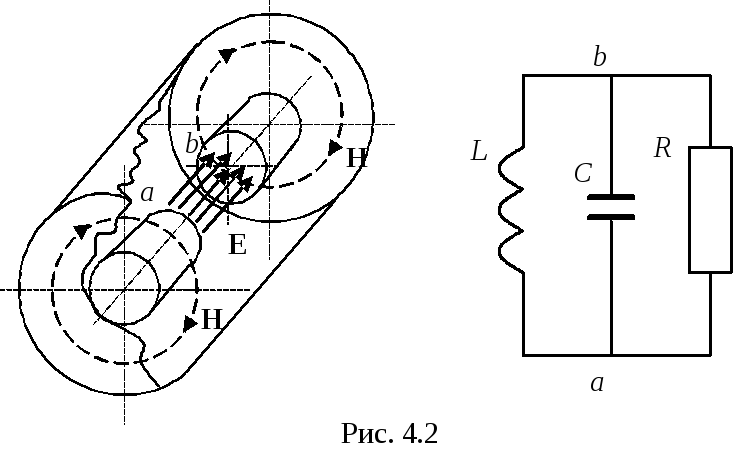ыражения

.

Теоретический расчет параметров резонаторов с произвольной формой поверхностей весьма сложен и может быть выполнен только численными методами с помощью специальных программных средств и даже при современном развитии компьютерной техники требует значительных временных ресурсов. Однако, учитывая аналогию между физическими процессами, протекающими в объемном резонаторе вблизи одной из собственных частот и в низкочастотном колебательном контуре резонатор микроволнового диапазона можно представить в виде эквивалентной схемы с сосредоточенными параметрами. Значения параметров эквивалентной схемы зависит от выбора точек отсчета, относительно которых она строится и от распределения поля данного вида колебаний.

Как уже отмечалось, у резонаторов специальной формы, в частности, у тороидальных, у которых линейные размеры много меньше собственной длины волны, существует возможность выделить области локализации электрического и магнитного полей. Структура электрического и магнитного полей основного вида колебаний тороидального резонатора показана на рис. 4.2. У такого резонатора наблюдается четкая локализация электрического поля в центре – в зазоре его внутреннего проводника, а магнитного поля – на периферии резонатора.Поэтому эквивалентная схема тороидального резонатора, построенная относительно выбранных в его зазореточекaиb(см. рис. 4.2), имеет вид параллельного колебательного контура, основные параметры которого вблизи собственного частотыi-го рассчитываются по измеренным параметрам резонатора::

Если известны , то из приведенных формул можно найти параметры эквивалентной схемы. Части объема, где концентрируется энергия электрического и магнитного полей, эквивалентны, соответственно, емкости и индуктивности контура. Роль сосредоточенной емкости играет плоский зазор в центре резонатора, роль сосредоточенной индуктивности – объем периферийной части резонатора. Поэтому параметры,R, а следовательно, и собственные параметры тороидального резонаторана основном виде колебаний могут быть приближенно рассчитаны методами электростатики и магнитостатики исходя из размеров резонатора.

Собственная длина волны:

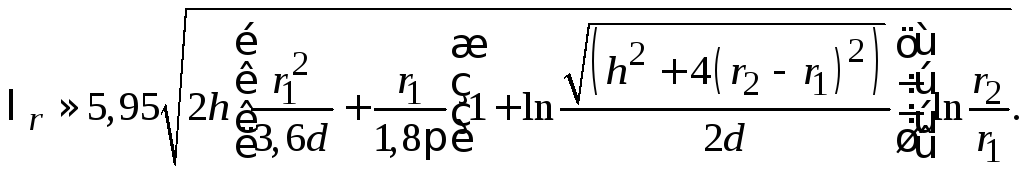
Добротность:

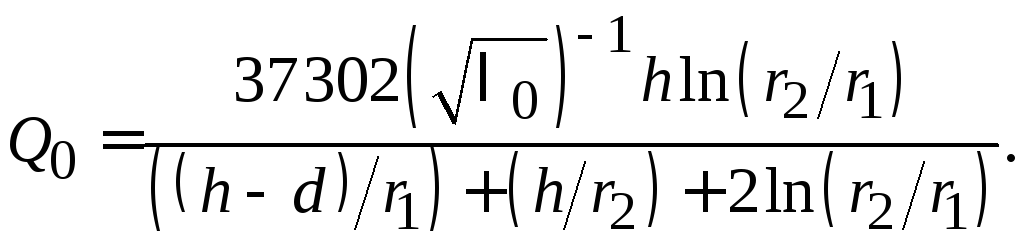
Волновое сопротивление:

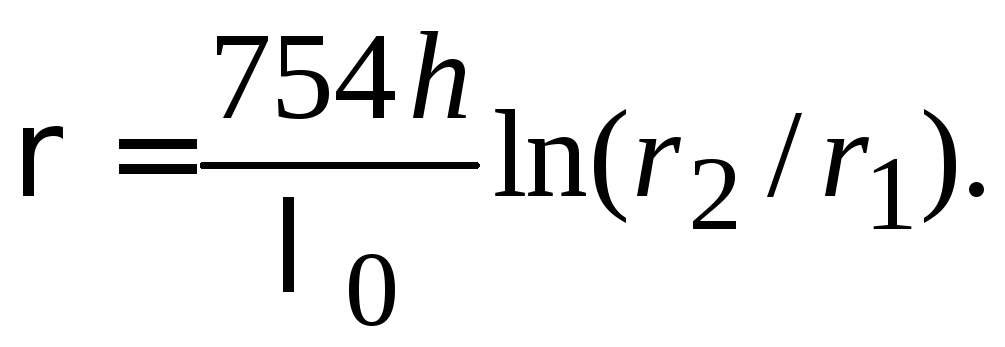
Размеры резонатора и длину волны в формулах , подставляют в сантиметрах, при этом волновое сопротивление получается в омах.

Если в объеме резонатора имеются источники поля (конвекционный ток) или он возбуждается от внешнего источника с помощью элемента связи, то в резонаторе возникают вынужденныеколебания. Поле этих колебаний можно представить в виде суперпозиции электромагнитных полей собственных колебаний

г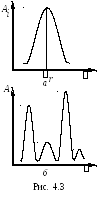де– потенциальные поля источников в объеме и поля отверстий в оболочке резонатора. Амплитудные коэффициентыипропорциональны величине

где – частота источника возбуждения,– комплексная собственная частота.. Частота, при которой функциядостигает максимума, называетсярезонансной, причем в свою очередьопределяется по формуле

Из этой формулы следует, что резонансная частота тем ближе к собственной, чем выше .Приразличие между этими частотами составляет менее 0.1%. Амплитуда вынужденных колебанийA в резонаторе на частотемаксимальна, а поле этих колебаний имеет структуру, близкую к структуре поля соответствующего собственного колебания с номером. Зависимость

,

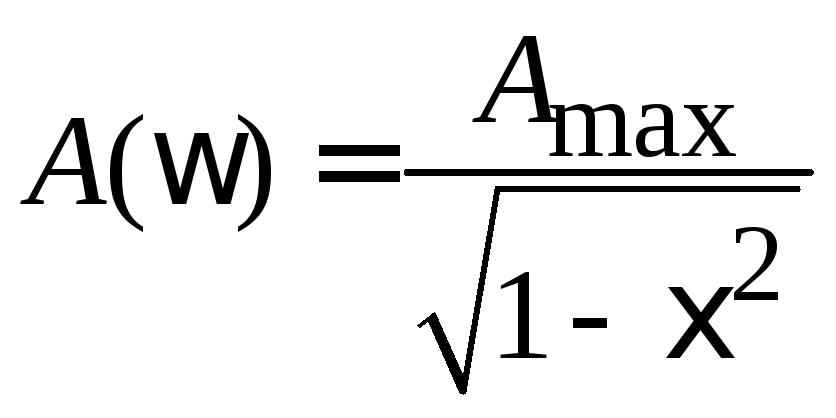где

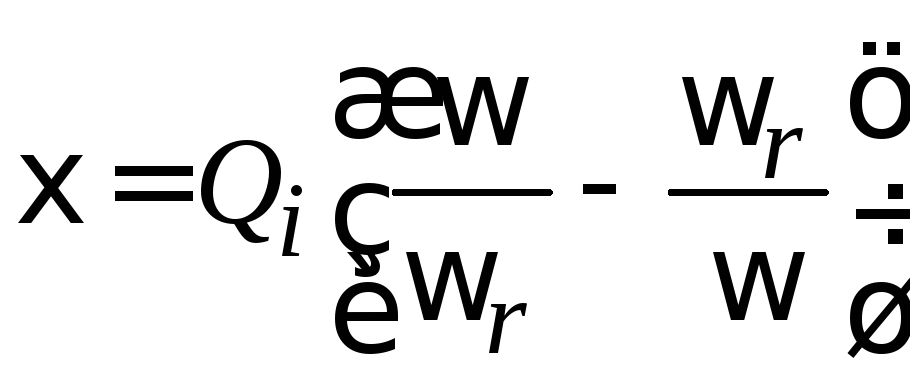
– обобщенная расстройка, имеет вид типичной резонансной кривой (рис. 4.3,а) и может рассматриваться как частотная характеристика резонатора вблизидля небольших номеров. В широкой полосе частот с увеличениемспектрсгущается и резонансные кривые различных видов колебаний перекрываются. Возможный вид характеристики в этом случае показан на рис. 4.3,б.

Таким образом, резонатор имеет множество резонансных частот, которые в случае малых потерь (больших ) приближенно равны частотам собственных колебаний. На практике наибольший интерес представляют виды колебаний с наименьшими резонансными частотами, достаточно удаленными друг от друга. Эти виды колебаний можно считать полностью разделенными и, следовательно, рассматривать независимо друг от друга.