67. Интегралы с бесконечными границами. Несобственные интегралы.

Опр.: Если интеграл от a до b стремится к определённому пределу при неограниченном возрастании b, то этот предел называется несобственным интегралом с бесконечной верхней границей. Несобственный интеграл – это предел определённого интеграла.

Св-ва:

1. Пусть f(x) – непрерывная на полуинтервале [a; +). Если с>a, то несобственный интеграл - сходятся или расходятся одновременно.

2. k=const, - сходятся или расходятся одновременно.

3. Интеграл суммы = сумме интегралов.

4. - обобщение формулы Ньютона-Лейбница.

Если первообразная не известна или не выражается в элементарных функциях, то для исследования на сходимость, нужно использовать признаки:

1. Пусть f и g – неотриц., непрерывные ф-и на [a; +), при чём f<g тогда если интеграл(g) – сходится, то и интеграл(f) – тоже сходится, если интеграл(f) – расходится, то и интеграл(g) – тоже расходится.

2.Пусть f и g>0 ф-и на [a; +). Тогда если lim(f/g)=k>0 но <+, то эти ф-ии сходится или расходятся одновременно.

3. Интеграл от модуля и интеграл без модуля – сх. и расх. одновременно.

68. Несобственный интеграл от неограниченной функции.

Опр.: Пусть ф-я f(x) неограниченна на отрезке [a,b] и непрерывны на любом отрезке [a,с], где a<c<b. Если существует конечный предел наз. несобственным интегралом от неограниченной ф-и и обозначается .

Св-ва такие же как и в предыдущем вопросе, только границы другие.

69. Функции многих переменных. Предел. Непрерывность. Теорема о непрерывных функциях.

1. n – мерное Эвклидово пространство

Опр.: Назовём n – мерной точкой упорядоченное множество из n действительных чисел. Расстояние между которыми вычисляется по формуле: (1).

Опр.: R_n – n-мерное ЕП наз. множество точек n-мерных точек, в которых введено расстояние по ф-ле (1).

Опр.: Ф-ей n переменных наз. отображение множества Х, включённого в n – мерное пространство.

График ф-ии n-переменных является пространство или его часть. Если ф-я задана с помощью ф-лы, то под областью определения понимается множество значений независимой переменной, при которых ф-я имеет смысл.

Увидеть важные св-ва графиков ф-й можно с помощью линий уровня.

2. Предел ф-ии рассмотрим на примере двух переменных.

Опр.: Число a называется пределом ф-ии f(M)=f(x,y) в точке M₀(x₀,y₀), если:

Опр.: Ф-я z=f(x,y) называется непрерывной в точке M₀(x₀,y₀), если: .

Опр.: Ф-я наз. непрерывной если её предел = значению ф-ии в этой точке.

Опр.: Если

Теор.(непрерывность сложной ф-ии): Если ф-ии - непрерывны в точке (s₀,t₀), а ф-я z=f(x,y) – непрерывна в точке (x₀,y₀), тогда сложная ф-я - тоже непрерывна в (s₀,t₀).

Док-во: Записать на основании определения непрерывностей, для всех ф-й неравенства.

70. Частные производные и их геометрический смысл. Производные по направлению. Градиент и его св-ва.

Пусть задана ф-я z=f(x,y). - частное приращение по переменной x.

Производные по направлению. Рассмотрим на плоскости точку M₀(x₀,y₀) и выходящий из неё луч L.

Опр.: Если существует конечный предел 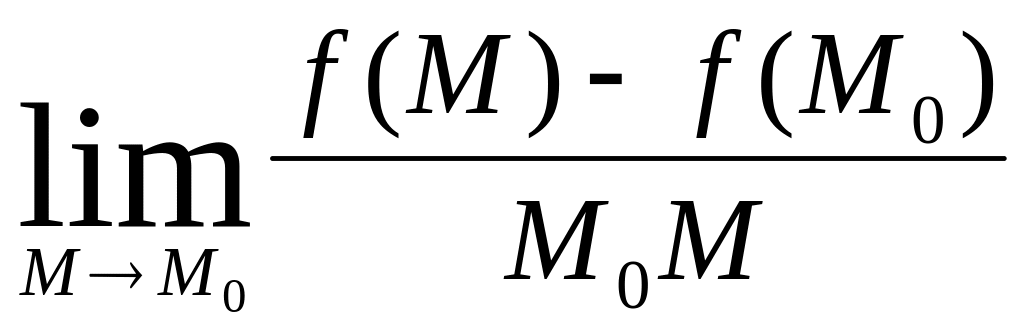, то этот предел называется производной по направлению .

Теор.: Если ф-я f(x,y) имеет в точке M₀(x₀,y₀) непрерывные частные, тогда существует производная по любому направлению , исходящему из точки M₀, которая вычисляется по ф-ле: .

Градиент. Пусть в каждой точке некоторой области определён скаляр, тогда говорят что задано скалярное поле. Градиентом скалярной ф-и z=f(x,y) наз. вектор, проекции которого на координатные оси совпадают с частными производными: ; .

Св-ва: Пусть - два скалярных поля имеющие градиент, а f – дифференцируемая скалярная ф-я. Тогда:

1.

2.

3.

4.