16. Свойства определенного интеграла.

Условимся, что a < b.

1. . То есть, значение определенного интеграла с совпадающими пределами интегрирования равно нулю.

2. . При перемене верхнего и нижнего пределов интегрирования местами значение определенного интеграла меняется на противоположное.

3. для интегрируемых на отрезке [a;b] функций y=f(x) и y=g(x).

4. Постоянный множитель можно выносить за знак определенного интеграла. .

5. Пусть функция y=f(x) интегрируема на интервале X, причем , тогда

.

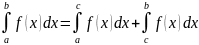6. Если функция интегрируема на отрезке [a; b], то она интегрируема и на любом внутреннем отрезке .

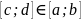7. Если функция y=f(x) интегрируема на отрезке [a;b] и для любого значения аргумента , то .

8. Пусть функция y=f(x) интегрируема на отрезке [a;b], тогда справедливо неравенство .

17. Формула Ньютона-Лейбница.

Пусть функция y=f(x) непрерывна на отрезке [a;b] и F(x) - одна из первообразных функции на этом отрезке, тогда справедливо равенство .

Эту формулу называют основной формулой интегрального исчисления.

18. Вычисление площадей плоских фигур в декартовых и полярных координатах.

Декартовые координаты

Площадь между графиками двух функций равна разности интегралов от этих функций в одинаковых пределах интегрирования

Площадь, заключённая между графиком непрерывной функции на интервале [a,b] и горизонтальной осью, может быть вычислена как определённый интеграл от этой функции:

Площадь, заключённая между графиками двух непрерывных функций f(x), g(x) на интервале [a,b] находится как разность определённых интегралов от этих функций:

Полярные координаты

В полярных координатах: площадь, ограниченная графиком функции 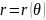и лучами вычисляется по формуле:

19. Вычисление объема тела по известному распределению площадей поперечных сечений. Объем тела вращения.

Известны площади сечений S(x) тела плоскостями

Объем тела вращения:

20. Вычисление длины дуги плоской кривой в прямоугольных координатах, параметрически заданной кривой и в полярных координатах.

Длиной дуги кривой линии называют предел, к которому стремится длина вписанной в нее ломаной линии при неограниченном увеличении числа ее звеньев и при стремлении длины наибольшего звена к нулю.

Прямоугольные координаты:

Параметрически заданной прямой

Полярные координаты

21. Комплексные числа

Ко́мпле́ксные чи́сла — расширение множества вещественных чисел, обычно обозначается . Любое комплексное число может быть представлено как формальная сумма x+iy, где x и y — вещественные числа, i — мнимая единица.

Сложение

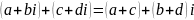
Вычитание

Умножение

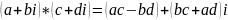
Деление

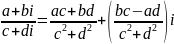
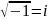, i*i=-1,

22. Обыкновенные дифференциальные уравнения. ДУ 1-ого порядка

Дифференциальное уравнение (ДУ) – это уравнение, в которое входит неизвестная функция под знаком производной или дифференциала.

Если неизвестная функция является функцией одной переменной, то дифференциальное уравнение называют обыкновенным

ДУ 11-ого порядка. F(x,y, y^/)=0 или y^/=f(x,y)

Общим решением ДУ называется такая функция ϕ(x,C) двух аргументов x и С, которая при постоянном С рассматривается как функция одного переменного.

23. Уравнение с разделяющимися переменными.

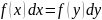Решение находится методом интегрирования обеих частей.

24. Однородные дифференциальные уравнения.

y^/=f(x,y) называется однородным относительно х и у, если функция f(x,y) является однородной степени 0.

25. Линейные ДУ 1-ого порядка (Бернулли, Лагранжа).

ЛДУ y^/(x)+f(x)y(x)=g(x)

Бернули: y^/+P(x)*y=Q(x)*y ; y=uv ; y^/=u^/v+v^/u

Лагранж: Метод вариации произвольной постоянной

26. Уравнение 2-ого порядка, допускающие понижение порядка.

1.

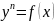
2.

3.

27. Однородные уравнения n-ого порядка

Все дифференциальные уравнения порядка выше первого называют дифференциальными уравнениями высших порядков.

Общий вид:

28. Линейно независимые решения.

Если линейная комбинация 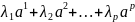представляет собой нулевой вектор только тогда, когда все числа равны нулю, то система векторов называется линейно независимой.

Определителем Вронского W(x;y₁(x),y₂(x),...,y_n(x)) называется определитель, первая строка которого образована функциями y₁(x), y₂(x), ..., y_n(x) из C_n-1[a,b] , а последующие строки образованы производными от функций предыдущей строки:

29. Линейные однородные уравнения 2-ого порядка с постоянными коэффициентами (3 случая)

, где p и q – произвольные действительные числа.

30. Линейные однородные уравнения 2-ого порядка с постоянными коэффициентами (построение частного решения в зависимости от правой части)

31. Область определения, способы задания и график функции 2-х переменных. Понятие поверхности в пространстве.

32. Частные приращения и частные производные. Геометрический смысл частных производных функций 2-х переменных.

33. Производные высших порядков. Теорема о независимости смешанных производных от порядка дифференцирования.

34. Экстремумы функций 2-х переменных. Наибольшее и наименьшее значения функции, непрерывной в замкнутой ограниченной области.

35. Частные и полный дифференциалы функций 2-х переменных. Применение полного дифференциала в приближенных вычислениях.

36. Дифференцирование сложных функций. Дифференцирование неявных функций.

37. Касательная плоскость и нормаль к поверхности, заданной в явном и неявном виде.

38. Производная по направлению. Градиент.