- •Системы счисления
- •Урок 2. Таблицы истинности. Логические схемы
- •III. Изложение нового материала
- •1. Таблицы истинности
- •Урок 3. Логические законы и правила преобразования логических выражений
- •5.5. Совершенная дизъюнктивная нормальная форма (сднф) и совершенная конъюнктивная нормальная форма (скнф)
- •5.5.1. Алгоритм образования сднф по таблице истинности
- •5.5.2. Алгоритм образования скнф по таблице истинности
- •3. Построение логических схем
Урок 3. Логические законы и правила преобразования логических выражений
|
|
А≡ А |
(А≡А) |
Закон тождества |
|
|
A&Ā=0 |
(А ∙ А= 0) |
Закон непротиворечия |
|
|
A v Ā=l |
(A+ А= 1) |
Закон исключающего третьего |
|
|
_ Ā=A |
|
Закон двойного отрицания |
|
|
А& 0= 0 Av0=A |
А∙ 0= 0 A+0=A |
|
|
|
А& 1= A Аv 1= 1 |
А∙ 1= A А+ 1= 1 |
|
|
|
А& A= A Аv A= A |
А ∙A= A А+ A= A |
|
|
|
Аv Ā= 1 |
А+ Ā= 1 |
Закон Моргана |
|
|
______ _ (A→B)=A&B |
______ _ (A→B)=A∙B |
|
|
|
A→B=Ā v B |
A→B=Ā+B |
|
|
|
A&(A v B)=A |
A∙(A+B)=A |
Закон поглощения |
|
|
A v A&B = A |
A+A∙B = A |
Закон поглощения |
|
|
Ā&(AvB) = Ā&B |
Ā∙(A+B) = Ā∙B |
|
|
|
AvĀ&B = AvB |
A+Ā∙B = A+B |
|
|
|
(AvB) vC =Av(BvC) (A&B)&C = A&(B&C) |
(A+B)+C=A+(B+C) (A∙B)∙C = A∙(B∙C) |
Правило ассоциативности |
|
|
(A&B) v(A&C) = A&(BvC) |
(A∙B) +(A∙C) = A∙(B+C) |
Правило дистрибутивности |
|
|
AvA = A A&A = A |
A+A = A A∙A = A |
Правило идемпотентности |
|
|
A v B=B v A A&B=B&A |
A+B=B+A A∙B=B∙A |
Правило коммутативности |
|
|
____ A≡B = A &B v A& В = (Ā+B) &(A+B) |
|
|
Если логическое выражение содержит большое число операций, то составлять для него таблицу истинности достаточно сложно, так как приходится перебирать большое количество вариантов. В таких случаях формулы удобно привести к нормальной форме.
Формула имеет нормальную форму, если в ней отсутствуют знаки эквивалентности, импликации, двойного отрицания, при этом знаки отрицания находятся только при логических переменных.
Для приведения формулы к нормальной форме используют законы логики и правила логических преобразований.
Пример 1
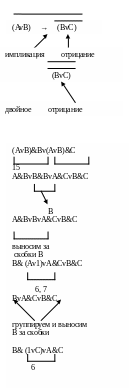
Упростите логическое выражение F= ¬((A v B)→ ¬(B v C)).
Это логическое выражение необходимо привести к нормальной форме, т.к. в нем присутствует импликация и отрицание логической операции.
(AvB)→(BvC)= (AvB)&(BvC).
( A v В) & (В v С) = (A v В) & (B v С).
(A v В) & (B v С)= (AvB)&Bv(AvB)&C
( AvB)&Bv(AvB)&C = A&BvB&BvA&CvB&C.
A&BvB&BvA&CvB&C= A&BvBvA&CvB&C
A&BvBvA&CvB&C= B& (Av1)vA&CvB&C.
B& (Av1) vA&CvB&C= BvA&CvB&C.
BvA&CvB&C = B& (1vC)vA&C.
B&(1vC)vA&C=BvA&C. |
|
Ответ: F= ¬((AvB)→ ¬(BvC))= BvA&C.
Выражение: F = ¬ (А&В) v ¬ (В&С).
Ответ: F = ¬ (A&B) v ¬ (В&С) =AvBvBvC =AvBvC.
Выражение: F = ¬ (X&YvY&Z)vZ&X.
Ответ: F = ¬ (X&YvY&Z)vZ&X= ¬ (Y&(YvZ))vZ&X= ¬Yv(XvY)vZ&X=
= YvX&ZvZ &X= YvX& (ZvZ) =Yv X.
Упростим формулу (А →B&С) & (С → В& А) & (В→С&А)=
= (А& B vС & A& A v В& C & В v B& С&C&A) & ( C v B&A) =
= A& В& (C v B &A) = A& В& C v A& В& B&A = A&В&C