
- •1 Предел и непрерывность функций нескольких переменных
- •2Частные производные функции нескольких переменных
- •3 Дифференциал функции нескольких переменных
- •4Дифференцирование сложных функций.
- •5 Дифференцирование функций, заданных неявно.
- •6 Касательная плоскость и нормаль к поверхности
- •8Формула Тейлора для функций нескольких переменных.
- •9Условный экстремум функции нескольких переменных
- •10Определение вероятности
- •11Геометрическое определение вероятности
- •12Формула полной вероятности.
- •13Элементы комбинаторики
- •14Схема Бернулли
- •15Теоремы Муавра-Лапласа
- •16 Дискретная случайная величина и закон ее распределения
- •17 Непрерывные случайные величины
- •18Числовые характеристики случайных величин.
- •19 Cм 18Дисперсия случайной величины
- •23Среднее арифметическое
19 Cм 18Дисперсия случайной величины
Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.
Если случайная величина x имеет математическое ожидание Mx , то дисперсией случайной величины x называется величина Dx = M(x - Mx )2.
Легко показать, что Dx = M(x - Mx )2= Mx 2 - M(x )2.
Эта универсальная формула одинаково хорошо применима как для дискретных случайных величин, так и для непрерывных. Величина Mx 2 >для дискретных и непрерывных случайных величин соответственно вычисляется по формулам
,
.
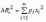
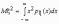
Для
определения меры разброса значений
случайной величины часто используется
среднеквадратичное отклонение ,
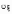 связанное с дисперсией соотношением
.
связанное с дисперсией соотношением
.
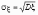
Основные свойства дисперсии:
дисперсия
любой случайной величины неотрицательна,
Dx
 0;
0;
дисперсия константы равна нулю, Dc=0;
для произвольной константы D(cx ) = c2D(x );
дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: D(x ± h ) = D(x ) + D (h ).
20Дисперсия, как характеристика разброса случайной величины, имеет один недостаток. Если, например, Х – ошибка измерения имеет размерность ММ2, то дисперсия имеет размерность . Поэтому часто предпочитают пользоваться другой характеристикой разброса – средним квадратическим отклонением, которое равно корню квадратному из дисперсии.
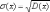
Среднее квадратическое отклонение имеет ту же размерность, что и сама случайная величина.
Кроме математического ожидания и дисперсии, для оценки случайной величины используются начальные и центральные моменты случайной величины.
Начальным
моментом порядка
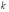 случайной величины
случайной величины
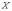 называют математическое ожидание
величины :
называют математическое ожидание
величины :
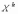
.

Центральным моментом порядка случайной величины называют математическое ожидание величины :
.

Начальный момент первого порядка равен математическому ожиданию самой случайной величины .
Центральный момент первого порядка равен нулю:
.
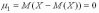
Централный момент второго порядка представляет собой дисперсию случайной величины
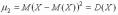
Для дискретных случайных величин:
;
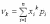
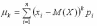
Коэффицие́нт асимметри́и (skewness) — числовая характеризующая степени несимметричности распределения данной случайной величины.
Определение
Пусть
задана случайная величина
 ,
такая что .
,
такая что .
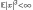
Коэффициент асимметрии распределения случайной величины определяется формулой:
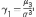
где
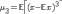 —
третий
центральный момент случайной величины
;
—
третий
центральный момент случайной величины
;
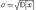 — стандартное
отклонение случайной величины
;
— стандартное
отклонение случайной величины
;
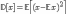 —
дисперсия
или второй центральный момент случайной
величины
;
—
дисперсия
или второй центральный момент случайной
величины
;
Если
плотность распределения симметрична,
то .
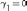
Если
левый хвост распределения тяжелее, то
.
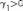
Если
правый хвост распределения тяжелее,
то .
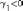
Иногда
вместо используется обозначение .
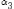
Эксцесс
Нормальное распределение наиболее часто используется в теории вероятностей и в математической статистике, поэтому график плотности вероятностей нормального распределения стал своего рода эталоном, с которым сравнивают другие распределения. Одним из параметров, определяющих отличие распределения случайной величины x , от нормального распределения, является эксцесс.
Эксцесс
g случайной величины x определяется
равенством
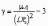 .
.
У нормального распределения, естественно, g = 0. Если g (x ) > 0, то это означает, что график плотности вероятностей px (x) сильнее “заострен”, чем у нормального распределения, если же g (x ) < 0, то “заостренность” графика px (x) меньше, чем у нормального распределения.
21Математическая статистика – это наука, занимающаяся методами обработки экспериментальных данных. Любая наука решает в порядке возрастания сложности и важности следующие задачи:
1) описание явления;
2) анализ и прогноз;
3) поиск оптимального решения.
Такого рода задачи решает и математическая статистика:
1) систематизировать полученный статистический материал;
2) на основании полученных экспериментальных данных оценить интересующие нас числовые характеристики наблюдаемой случайной величины;
3) определить число опытов, достаточное для получения достоверных результатов при минимальных ошибках измерения.
Одной из задач третьего типа является задача проверки правдоподобия гипотез. Она может быть сформулирована следующим образом: имеется совокупность опытных данных, относящихся к одной или нескольким случайным величинам. Необходимо определить, противоречат ли эти данные той или иной гипотезе, например, гипотезе о том, что исследуемая случайная величина распределена по определенному закону, или две случайные величины некоррелированы (т.е. не связаны между собой) и т.д. В результате проверки правдоподобия гипотезы она либо отбрасывается, как противоречащая опытным данным, либо принимается, как приемлемая.
Таким образом, математическая статистика помогает экспериментатору лучше разобраться в полученных опытных данных, оценить, значимы или нет определенные наблюденные факты, принять или отбросить те или иные гипотезы о природе рассматриваемого явления.
Генеральная и выборочная совокупности
Исходным понятием статистики является понятие совокупность, объединяющее обычно какое-либо множество испытуемых (учащихся) по одному или нескольким интересующим признакам. Главное требование к выделению изучаемой совокупности — это ее качественная однородность, например, по уровню знаний, росту, весу и другим признакам. Члены совокупности могут сравниваться между собой в отношении только того качества, которое становится предметом исследования. При этом обычно абстрагируются от других неинтересующих качеств. Так, если педагога интересует успеваемость учащихся, то он не принимает во внимание, как правило, их рост, вес и другие параметры, не относящиеся непосредственно к изучаемому вопросу.
Применение большинства статистических методов основано на идее использования небольшой случайной совокупности испытуемых из общего числа тех, на которых можно было бы распространить (генерализовать) выводы, полученные в результате изучения совокупности. Эта небольшая совокупность в статистике называется выборочной совокупностью (или короче —выборкой). Главный принцип формирования выборки — это случайный отбор испытуемых из мыслимого множества учащихся, называемого генеральной совокупностью или популяцией объектов или явлений. Как по анализу элементов, содержащихся в капле крови, медики нередко судят о составе всей крови человека, так и по выборочной совокупности учащихся изучаются явления, характерные для всей генеральной совокупности.
Когда для каждого объекта в выборке измерено значение одной переменной, популяция и выборка называются одномерными. Если же для каждого объекта регистрируются значения двух или нескольких переменных, такие данные называются многомерными.
Одной из основных задач статистического анализа является получение по имеющейся выборке достоверных сведений о интересующих исследователя характеристиках генеральной совокупности. Поэтому важным требованием к выборке является ее репрезентативность, то есть правильная представимость в ней пропорций генеральной совокупности. Достижению репрезентативности может способствовать такая организация эксперимента, при которой элементы выборки извлекаются из генеральной совокупности случайным образом.
Обычно в статистике различают три типа значений переменных: количественные, номинальные и ранговые.
Значения количественных переменных являются числовыми, могут быть упорядочены и для них имеют смысл различные вычисления (например, среднее значение). На обработку количественных переменных ориентировано подавляющее большинство статистических методов.
Значения номинальных переменных (например: пол, вид, цвет) являются нечисловыми, они означают принадлежность к некоторым классам и не могут быть упорядочены или непосредственно использованы в вычислениях. Для анализа номинальных переменных специально предназначены лишь избранные разделы математической статистики, например, категориальный анализ. Однако в ряде случаев для этой цели могут быть использованы и некоторые ранговые и количественные методы, если номинальные значения предварительно заменить на числа, обозначающие их условные коды.
Ранговые или порядковые переменные занимают промежуточное положение: их значения упорядочены (состояние больного, степень предпочтения), но не могут быть с уверенностью измерены и сопоставлены количественно. К анализу ранговых переменных применимы так называемые ранговые методы.
Ранг наблюдения – это тот номер, который получит данное наблюдение в упорядоченной совокупности всех данных – после их упорядочивания по определенному правилу (например, от большего значения к меньшим). Процедура перехода от совокупности наблюдений к последовательности их рангов называется ранжированием.
Ранговые и номинальные значения при вводе данных следует обозначать целыми числами.
