Задача 4

По заданию k = 8 и t_u = 3.

Решая систему уравнений:

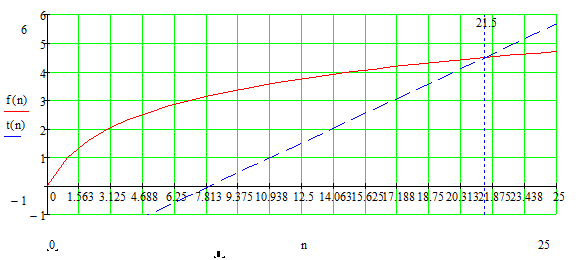
Получим, что n=21 приблизительною. Из [3] по таблице 8.1.6 на странице 373 определим n, k, t наиболее близкие к исходным данным:

n=31

k=11

tu=5

В соответствии с данными образующий многочлен g(р)=5423325, переведем в двоичный код. Отсюда g(x): 1 0110 0010 0110 1101 0101.

Рис.10 Схема кодера

Проверка:

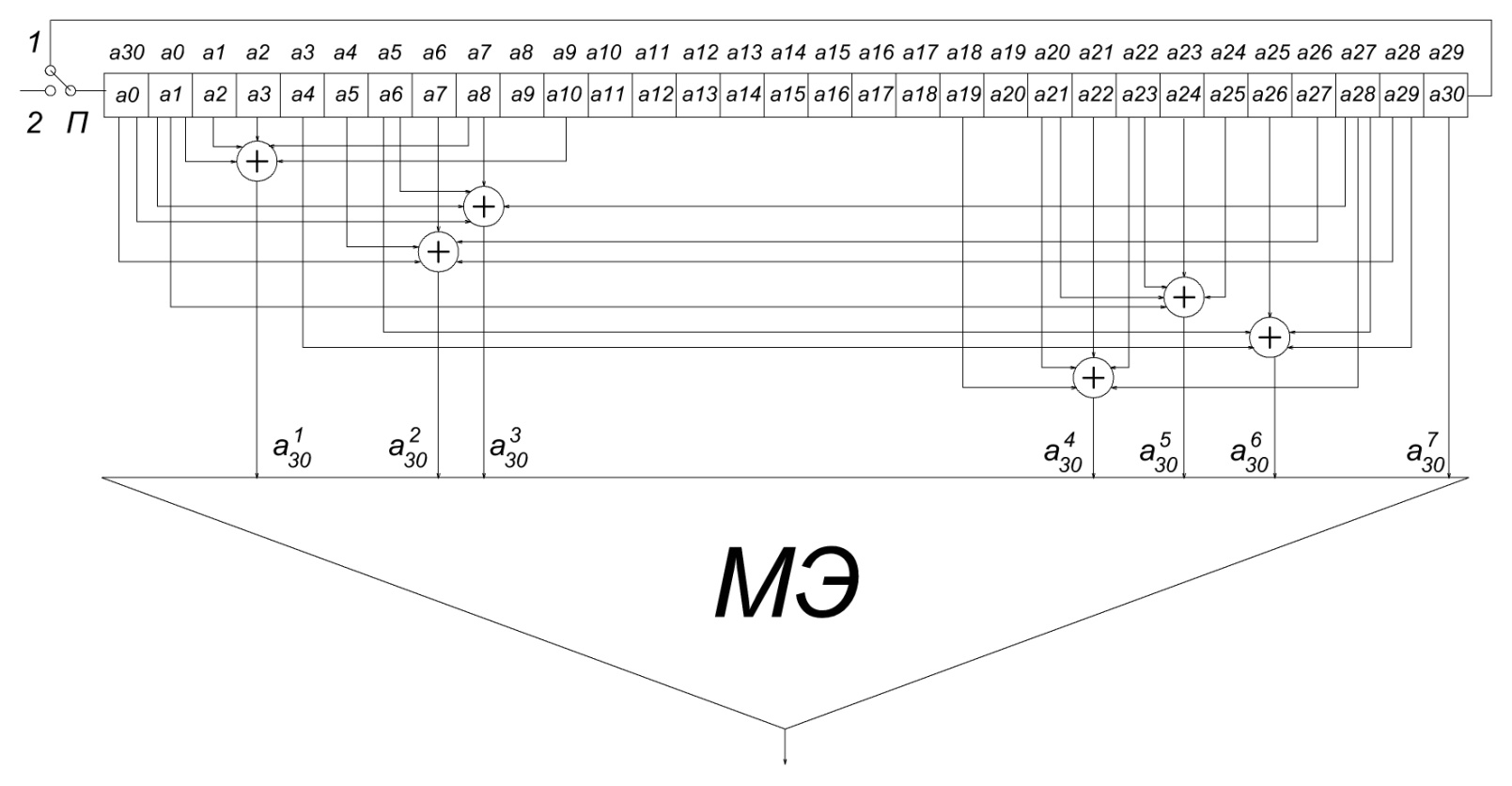
Рис.11 Схема декодера

График появления необнаруживаемой ошибки при заданном изменении вероятности ошибки в канале связи (рис.13)

Оценим вероятность получения обнаруживаемой ошибки на выходе системы:

_{График появления необнаруживаемой ошибки при заданном изменении вероятности ошибки в канале связи}[4]:

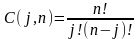_{(12) - Сочетание из n по j элементов}

(13) – Вероятность необнаруживаемой ошибки

Рис.13 График появления необнаруживаемой ошибки при заданном изменении вероятности ошибки в канале связи

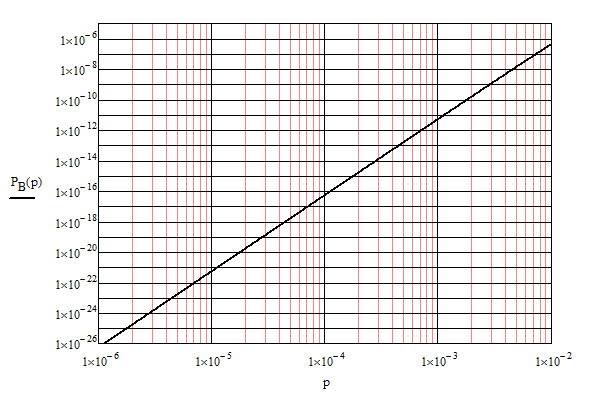
По полученному графику можно сделать вывод, что с увеличением вероятности ошибок в канале, растет вероятность получить необнаруживаемую ошибку. Список используемой литературы:

1. Лекции ОПДС, лектор Езерский В.В.

2. Основы передачи дискретных сообщений: Учебник для вузов/ Ю.П. Куликов, В.М. Пушкин, Г.И. Скворцов и др.: Под ред. В.М. Пушкина. – М.: Радио и связь, 1992.- 288 с., ил.

3. Прокис Дж. Цифровая связь.  М.: Радио и связь, 2000.

4. Скляр Б. Цифровая связь.  М., Санк-П, Киев: Изд. дом «Вильямс», 2003.

5. Кодирование и декодирование циклических кодов. № 4086 . Рязань. РГРТУ. 2008 г.

6. Исследование устройств синхронизации в СПДС. № 3874. Рязань. РГРТУ. 2006 г.

7. Виды и протоколы модуляции в системах передачи дискретных сообщений. № 3980. Рязань. РГРТУ. 2007 г.