Добавил:

Studfiles2 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

Теория вероятностей и математическая статистика

Файл:

Методические указания по теории вероятностей / 2008-04-16-08-34-я- указания

.pdf

Скачиваний:

212

Добавлен:

01.05.2014

Размер:

358.64 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 33

5.	Если все возможные значения случайной величины Х находятся на
	интервале (а, b), то F(x)=0 при х≤а и F(x)=1 при x ≥ b .
6.	lim F(x) = 0 ,	lim F(x) =1.
	x→−∞	x→+∞

Плотностью распределения непрерывной случайной величины Х называют производную от функции распределения: f (x) = F ′(x) .

Плотность распределения непрерывной случайной величины Х обладает свойствами:

1. f(x)≥0.

	+∞
2.	∫ f (x)dx =1.
	−∞
3.	Зная плотность распределения, можно найти функцию распределения
		x
	случайной величины F(x) = ∫ f (x)dx .
		−∞
	b
4. P(a < X < b) = ∫ f (x)dx .
	a
Примеры. 1. Случайная величина Х задана функцией распределения
		0		при x ≤ 2,
			2	при 2 < x ≤ 3,
	F(x) = (x −2)			при 2 < x ≤ 3,
		1		при x > 3.
		1		при x > 3.

Найти плотность распределения этой случайной величины и вероятность попадания ее в интервал (1; 2,5).

По определению				0	при x < 2,
				0	при x < 2,
′					при 2 < x < 3,
f (x) = F (x) = 2(x −2)					при 2 < x < 3,
				0	при x > 3.
Требуемая вероятность будет				0	при x > 3.
Требуемая вероятность будет						1		1
P(1 < X < 2,5) = F(2,5) − F(1) =						1	−0 =	1	.
P(1 < X < 2,5) = F(2,5) − F(1) =							−0 =	4	.
					4			4
2. Дана плотность распределения непрерывной случайной величины Х:
		0		при	x ≤1,
			1
f (x) = x −			1	при 1 < x ≤ 2,
f (x) = x −		2		при 1 < x ≤ 2,
		2		при x > 2.
		0		при x > 2.
Найти функцию распределения этой величины.
				x
Воспользуемся формулой	F(x) = ∫ f (x)dx .

−∞

Если х≤1, то f(x)=0, следовательно, F(x) = ∫0dx = 0 .

−∞

Если 1<x≤2, то																			x
x		0				x			1			t 2			1							1	(x		2	− x).
x		0				x			1			t 2			1							1			2
F(x) = ∫ f (x)dx = ∫0dx + ∫							t −				dt =			−			t				=
F(x) = ∫ f (x)dx = ∫0dx + ∫							t −		2		dt =		2	−	2		t				=	2
−∞		−∞				0			2				2		2				0			2
Если х>2, то																			0					2
Если х>2, то
x	0				2			1				x				1		(x		2	− x)


F(x) = ∫ f (x)dx = ∫0dx + ∫ x −										dx +		∫0dx =												=1.
F(x) = ∫ f (x)dx = ∫0dx + ∫ x −										dx +		∫0dx =												=1.
−∞	−∞				0			2				2				2								0
−∞	−∞				0			2				2				2								0
Итак, искомая функция распределения имеет вид
					0		при			x ≤1,
F(x) =		1	(x	2	− x) при 1 < x ≤ 2,

		2
		2			1	при x > 2.
					1	при x > 2.

3. Составить функцию распределения F(x) дискретной случайной величины Х с законом распределения:

Х	2	4	7
Р	0,5	0,2	0,3

Если х≤2, то F(x)=0, так как значений меньших 2 величина Х не принимает. Поэтому при х≤2 F(x)=Р(Х<x)=0.

Если 2<x≤4, то F(x)=0,5, так как Х может принимать значение 2 с вероятностью 0,5.

Если 4<x≤7, то F(x)= Р(Х<x)= Р(Х=2)+ Р(Х=4)=0,5+0,2=0,7 (по теореме сложения вероятностей несовместных событий).

Если х>7, то F(x)=1, так как событие Х≤7 достоверное. Итак, искомая функция распределения имеет вид

	0	при	x ≤ 2,
		при	2 < x ≤ 4,
0,5
F(x) =		при	4 < x ≤ 7,
0,7
	1	при	x > 7.

Числовые характеристики непрерывной случайной величины

Аналогично тому, как это было сделано для дискретной случайной величины, определим числовые характеристики непрерывной случайной величины Х с плотностью распределения f(x).

Математическим ожиданием непрерывной случайной величины Х с плотностью распределения f(x) называется выражение

+∞

M [ X ] = ∫xf (x)dx .

−∞

Если случайная величина Х может принимать значения только на ко-

нечном отрезке [a, b], то M [ X ] = ∫xf (x)dx .

Дисперсия непрерывной случайной величины Х определяется равенст-

вом

D[ X ] = M [X − M ( X )]2 = +∞∫(x − M [ X ])2 f (x)dx ,

−∞

или равносильным равенством

+∞

D[ X ] = ∫x2 f (x)dx −(M [ X ])2 .

−∞

Все свойства математического ожидания и дисперсии, указанные для дискретных величин, сохраняются и для непрерывных величин

Среднеквадратичным отклонением случайной величины Х называется корень квадратный из дисперсии

σ[ X ] = D[ X ] .

Значение случайной величины Х, при котором плотность распределения f(x) имеет наибольшее значение называется модой М0[X].

Медианой Ме[X] непрерывной случайной величины Х, называют ее значение, определяемой равенством

P( X < M e [ X ]) = P( X > M e [ X ])

или

M e	+∞	1
∫ f (x)dx =	∫ f (x)dx =		.
		2
−∞	M e

Пример. Случайная величина Х задана плотностью распределения

	0		при x ≤ 0,
	1
f (x) = x −		x3	при 0 < x < 2,
	4
			при x ≥ 2.
	0

Найти математическое ожидание, дисперсию и среднеквадратичное отклонение величины Х.

Воспользуемся определениями.

		+∞			2			1			3						1			3				1				5	2		8			8		16
		+∞			2			1			3						1			3				1				5	2		8			8		16
M [ X ] = ∫xf (x)dx = ∫x x						−			x			dx =							x		−					x				=			−		=		.
M [ X ] = ∫xf (x)dx = ∫x x						−		4	x			dx =					3		x		−		20			x				=	3		−	5	=	15	.
		−∞			0																								0
					0																								0
	2	+∞	2		2	2					1			3							1			4				1		6		2		4
	2	+∞	2		2	2					1			3							1			4				1		6		2		4
M [ X		] = ∫x		f (x)dx = ∫x			x		−				x		dx =							x			−				x				=		.
M [ X		] = ∫x		f (x)dx = ∫x			x		−		4		x		dx =						4	x			−		24		x				=	3	.
		−∞			0																											0
					0																											0
D[ X ] = M [ X 2 ] − M 2 [ X ] =							4	−		256				=		44		.
D[ X ] = M [ X 2 ] − M 2 [ X ] =							3	−	225					=				.
							3		225						225
σ[ X ] = D[ X ] =					2 11 .
					15

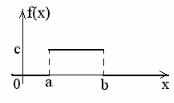
Закон равномерного распределения вероятностей непрерывной случайной величины

Непрерывная случайная величина Х имеет равномерное распределение вероятностей если ее плотность распределения задается следующим образом:

при

a ≤ x ≤ b,

f (x) =

при

x < a,

x > b.

Найдем значение с. По свойству плотностей

распределения

+∞∫ f (x)dx =1 получаем

−∞

+∞

∫ f (x)dx = ∫cdx = c(b −a) =1,

−∞

следовательно,

c =

−a

при a ≤ x ≤ b,

f (x) =

b −a

при x < a, x

> b.

Так как b −a =

, то промежуток [a, b], на котором имеет место равно-

мерное распределение, обязательно конечен.

Определим вероятность того, что случайная величина Х примет значе-

ние, заключенное в интервале (α, β).

dx = β −α .

P(α

< X < β) = ∫

f (x)dx = ∫ 1

b −a

Итак, искомая вероятность

β −α

P(α < X

< β) =

b −a

т.е. вероятность попадания Х в интервал зависит только от длины этого интервала и не зависит от значений величины Х. При равномерном распределении случайной величины Х вероятности попадания Х в промежутки равной длины одинаковы.

						x
Найдем функцию распределения F(x) = ∫ f (x)dx .
						−∞
Если х<a,	то f(x)=0	и, следовательно,			F(x) = 0 .
Если а≤x≤b, то f (x) =			1	и, следовательно,
Если а≤x≤b, то f (x) =			b −a	и, следовательно,
			b −a	F(x) = ∫x	1		x −a
					1	dx =	x −a	.
						dx =		.
Если х>b,	то f(x)=0			a b −a			b −a
Если х>b,	то f(x)=0	и, следовательно,

F(x) = ∫b		1	dx + ∫x 0dx =			b −a	=1.
						b −a
a b −a				b
Таким образом,		0		при	x < a,

		−a
F(x) =	x			при a ≤ x ≤ b,

b −a				при x > b.
		1

Пример. Интервал движения автобуса равен 20 минутам. Найти вероятность того, что пассажир будет ожидать автобус менее 5 минут.

Пусть случайная величина Х – время прихода пассажира на станцию после отправления очередного автобуса 0<X<20. Х имеет равномерное распределение, так как вероятность прихода, например, в пятую минуту, равна вероятности прихода в восьмую. В задаче требуется найти вероятность того, что случайная величина Х примет значение из интервала (15, 20).

P(15 < X < 20) = 205 = 0,25 .

Числовые характеристики равномерного распределения

Для случайной величины Х, имеющей равномерное распределение, плотность распределения определяется формулой

f (x) =

при

≤ x

≤ b,

b −a

x < a, x

> b.

при

Тогда по определению математического ожидания

+∞

b2 −a2

a +b

M [ X ] = ∫xf (x)dx = ∫x

dx =

b −a

2(b −a)

−∞

+∞

−a

+ab +b

M [ X 2 ] = ∫x2 f (x)dx = ∫x2

dx =

b −a

3(b −a)

−∞

Дисперсия равномерно распределенной случайной величины будет

D[ X ] = M [ X 2 ] − M 2 [ X ] =

a2 + ab +b2

−

a2 + 2ab +b2

a2 −2ab +b2

(b −a)2

Итак,

(b −a)2

σ[ X ] = b −a .

M [ X ] =

a +b

D[ X ]=

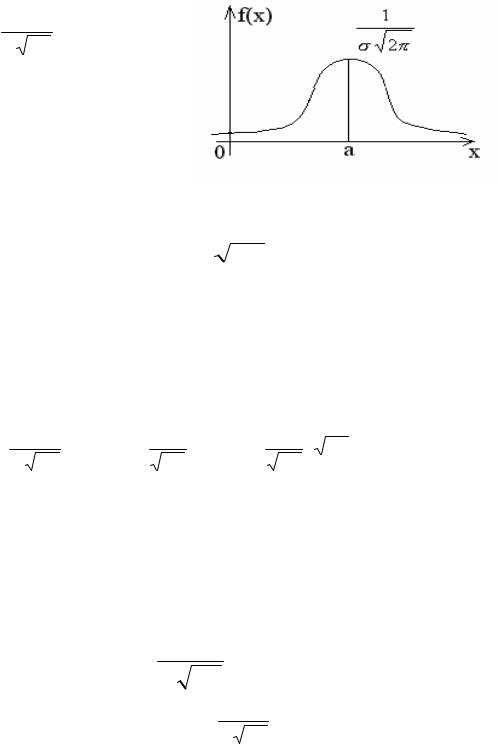
Нормальный закон распределения непрерывной случайной величины

Изучение различных явлений показывает, многие случайные величины, например, такие, как погрешности при измерениях, величина износа деталей во многих механизмах и т.д., имеет плотность распределения вероятности, которая определяется формулой

	f (x) =		1	e−	( x−a )2	,
	f (x) =		1	e−	2σ 2	,
			σ 2π
где	а	и	σ	–	параметры
распределения. В этом случае
говорят, что случайная величина Х
подчинена		нормальному				закону
распределения.			Кривая нормального
распределения			изображена					на
рисунке.
	В дальнейшем нам потребуется интеграл Пуассона
						+∞	−	t 2		2 π .
						∫ e			dt =
						∫ e		2	dt =

− ∞

Используя этот интеграл несложно заметить, что функция распределе-

ния f(x) удовлетворяет основному соотношению

+∞

∫ f (x)dx =1.

x −a

−∞

Действительно, обозначив

= t,

dx =σdt , можно написать

+∞

e−

( x−a )2

+∞

−

t 2

∫

2σ 2

dx =

∫e

dt =

2π =1.

−∞σ

2π

−∞

2π

Числовые характеристики нормального распределения

Определим математическое ожидание случайной величины с нормаль-

ным законом распределения

f ( x) =		1	e−	( x −a )2
f ( x) =	σ	1	e−	2σ 2		.
	σ	2π				( x−a )2
+∞		+∞	1		e−	( x−a )2
M [ X ] = ∫xf (x)dx = ∫x			1		e−	2σ 2	dx .
−∞		−∞	σ 2π
Выполнив замену переменной		x −a	= t,	x = a +σt, dx =σdt , получа-
Выполнив замену переменной		σ	= t,	x = a +σt, dx =σdt , получа-
		σ

ем

+∞

−

+∞

−

+∞

−

t 2

M [ X ] =

∫(a +σt)e

dt =

∫e

dt +

∫te

dt =

2π

−∞

2π

−∞

+∞

2π

−∞

e−

2π −

= a .

2π

−∞

Итак, М[X]=a. Значение параметра а в формуле, определяющей плотность распределения вероятности, равно математическому ожиданию рассматриваемой случайной величины. Точка х=а является центром распределения вероятностей, или центром рассеивания.

Найдем

+∞

−

( x−a )2

M [ X 2 ] = ∫x2 f (x)dx =

∫x2 e

2σ 2

dx .

−∞

σ 2π −∞

Выполнив ту же замену переменной, будем иметь

+∞

M [ X 2 ] =

∫(a2 +2aσt +σ 2 t2 )e−

dt =

2π

−∞

+∞

t 2

+∞

∫e

−

dt + 2aσ

∫te−

dt + σ

∫t2 e−

dt = a

2 +0 +

∫t te

−

dt .

2π

−∞

2π

−∞

2π

−∞

2π

−∞

−t2

Проинтегрировав по частям последний интеграл: u=t, dv = te 2 dt , получим

M [ X 2	] = a2 +	σ 2
		2π

−t2

Так как по правилу Лопиталя lim te 2

t→∞

			t2	+∞
			t2	+∞
	−te	−
	−te	−	2

				−∞
				−∞
= 0 ,		то

+∞		t2
+ ∫e	−		dt
	−	2
				.
−∞
−∞

M [ X 2 ] = a2 +	σ 2	2π = a2	+σ 2 .
	2π

Поэтому дисперсия нормального распределения случайной величины будет

D[ X ] = M [ X 2 ] − M 2 [ X ] = a2 +σ 2 −a2 =σ 2 .

Итак, M[X]=a, D[X]=σ2, σ[X]= σ.

Функция Лапласа.

Функция распределения случайной величины Х, имеющей нормальное распределение

В дальнейшем будем использовать функцию Лапласа, определяемую равенством

	1	x	−	t2
Φ(x) =		∫e			dt .
				2
	2π	0

Составлены подробные таблицы значений этой функции. Укажем некоторые свойства функции Ф(х).

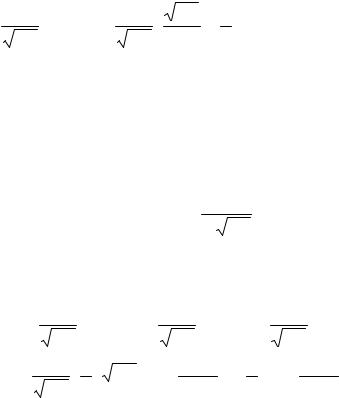
1.Ф(х) определена при всех значениях х.

2.Ф(0)=0.

+∞

2π

1 .

Φ(+∞) =

∫e−

dt =

2π

4. Φ(−∞) = −

Ф(х) монотонно возрастает при всех

x (−∞,+∞) .

Ф(х) – функция нечетная: Ф(-х)= - Ф(х).

Определим функцию распределения случайной величины Х, имеющей

нормальное распределение.

e−

( x−a )2

F(x) = ∫ f (x)dx = ∫

2σ 2

dx .

x −a

−∞

−∞σ

2π

Обозначив

= t,

получим

x−a

t 2

x−a

t 2

−

F(x) =

∫ e

dt =

∫e

dt +

∫ e

dt =

2π

−∞

2π

−∞

2π

x −a

2π

2π +Φ

+Φ

Итак, функция распределения случайной величины Х имеет вид

F(x) =	1	x −a
		+Φ		.
	2		σ

Вероятность попадания случайной величины Х, имеющей нормальное распределение,

в заданном интервале

Используя функцию распределения случайной величины Х, найдем вероятность попадания ее значений в интервал (α, β).

P(α < X < β) = F(β) − F(α) =

−a

x −a

+Φ

−

+Φ

β −a

α −a

= Φ

−Φ

β −a

α −a

Таким образом, P(α < X < β) = Φ

−Φ

Пример. Плотность распределения вероятностей случайной величины Х

−4 x2

+6 x−1

имеет вид f (x) =γ e

. Найти:

γ,

M[X],

D[X],

F(x),

−

< X <

Случайная величина Х имеет нормальное распределение. Поэтому при-

ведем плотность распределения f(x)

к виду

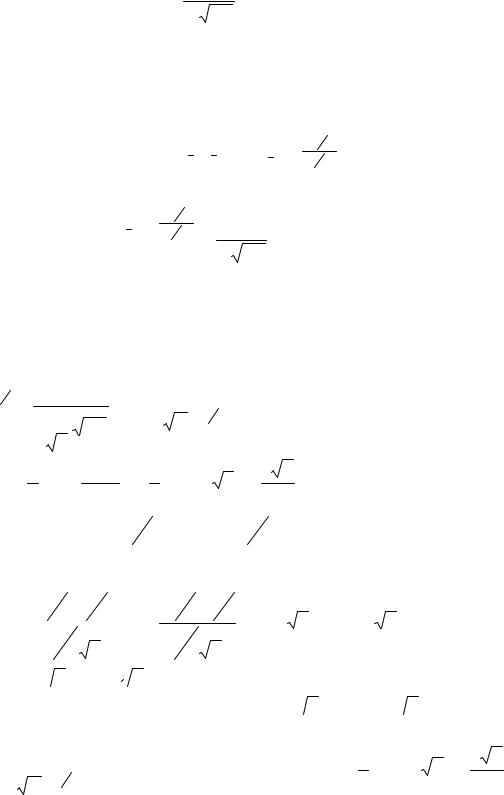
																							f (x) =												1						e−		( x−a )2
																							f (x) =							σ					1						e−			2σ 2			.
																														σ							2π
Выделим в показателе заданной функции полный квадрат
	2																2			3					1																		3			2			9						1			3	2	5
−4x		+6x	−1 = −4 x															−				x	+						= −4									x −										−					+			= −4 x	−		+		.
−4x		+6x	−1 = −4 x															−				x	+						= −4									x −										−					+			= −4 x	−		+		.
																				2					4																		4						16 4									4		4
Следовательно,																				2					4																		4						16 4									4		4
Следовательно,																																																		(x−3				)2
																																3		2			5								5					(x−3			4	)2
																											−4			−		3			+		5								5				−				4
															f (x) =γ e												−4		x	−		4			+		4			=γ e4 e											14 .
Сравним															f (x) =γ e																	4					4			=γ e4 e											14 .
Сравним																											(x−3				)2
																						5			−		(x−3			4	)2										1							( x−a )2
																						5			−					4															e−			( x−a )2
																		γ e4 e											14					=
																		γ e4 e											14					=				σ										2σ 2				.
Из последнего равенства получаем																																						σ			2π
Из последнего равенства получаем
		M [ X ] = a =										3			.
		M [ X ] = a =													.
							1				4																							1
		2σ 2 =					1		, т.е. D[ X ] =σ																				2 =					1		.
		2σ 2 =				4			, т.е. D[ X ] =σ																				2 =				8			.
						4																											8
		γ e	5		4	= 1					1										, γ =										2								.
		γ e			4	= 1											2π				, γ =								π e54										.
									2		2						2π
								1						x −a											1																			3 2
		F(x) =						1						x −a									=		1									2 2x −										3 2
		F(x) =						2		+Φ								σ					=		2			+Φ						2 2x −											2				.
								2										σ					5		2																− 3				2
				3									5										5	4		−a															− 3			4	−a
		P(−		3		< X <							5			) = Φ								4									−Φ											4							=
		P(−	4			< X <										) = Φ																	−Φ										σ								=
			4								4														σ																		σ

									5		4 −							3	4								−		3		4			−			3
											4 −								4								−				4			−						4		= Φ( 2) −Φ(−3 2) =
					= Φ																	−Φ
					= Φ						1											−Φ							1
											1							2											1			2					2
											2							2														2					2

=Φ( 2) +Φ(3 2) = 0,4207 +0,499968 = 0,921.

Впоследнем равенстве при вычислении Φ( 2) и Φ(3 2) использованы таблицы значений функции Ф(х).

					2				3		1			1			3 2
	Итак: γ		=		2		,	M [ X ] =	3	, D[ X ] =	1	,	F(x) =	1		2 2x −	3 2
															+Φ			,
					5				4		8			2	+Φ		2	,
	3		5		π e	4			4		8			2			2
P(−	3	< X <	5	) = 0,921.
P(−	4	< X <	4	) = 0,921.
	4		4

Литература

1.Пискунов Н.С. Дифференциальное и интегральное исчисления для ВТУЗОВ. М., 1962.

2.Гмурман В.Е. Теория вероятностей и математическая статистика.

3.Румшиский Л.З. Элементы теории вероятностей. М., 1966.

4.Севастьянов Б.А. Курс теории вероятностей и математической статистики.

М., 1982.

5.Чистяков В.П. Курс теории вероятностей. М., 1982.

6.Гмурман В.Е. Руководство по решению задач по теории вероятностей и математической статистике. М., 1975.

<<< < Предыдущая 1 23 / 33