Методические указания по теории вероятностей / 2008-04-16-08-34-я- указания

P( A) =1 − P( A) =1 − 16 = 65 .

Зависимые события. Условная вероятность. Формула полной вероятности

Событие А называется зависимым от события В, если вероятность появления события А зависит от того, произошло или нет событие В.

Вероятность того, что произошло А при условии, что произошло событие В, будем обозначать P(A/B) и называть условной вероятностью события А при условии В.

Например. В урне находятся 3 белых шара и 2 черных. Из урны вынимается один шар, а затем второй. Событие В – появление белого шара при первом вынимании. Событие А – появление белого шара при втором вынимании.

Очевидно, что вероятность события А, если событие В произошло, будет

P( A/ B) = 24 = 12 . Вероятность события А при условии, что событие В не произошло, будет P( A/ B) = 43 .

Справедливы следующие теоремы.

Теорема. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е.

P( AB) = P(B)P( A/ B) = P( A)P(B / A) .

В частности, отсюда получаем P( A/ B) = PP((ABB)) .

Теорема. Если событие А может произойти только при выполнении одного из событий В1, В2,…Вn, которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле

P( A) = P(B1 )P( A/ B1 ) + P(B2 )P( A/ B2 ) +... + P(Bn )P( A/ Bn ) .

Эта формула называется формулой полной вероятности.

Примеры. 1. Вероятность изготовления годного изделия данным станком 0,9. Вероятность появления изделия первого сорта среди годных изделий 0,8. Определить вероятность изготовления изделия первого сорта данным станком.

Событие В – изготовление годного изделия данным станком; событие А – появление изделия первого сорта. Очевидно, Р(В)=0,9, P( A/ B) = 0,8. Искомая вероятность будет

P( AB) = P(B)P( A/ B) = 0,9 0,8 = 0,72 .

2. К экзамену надо подготовить 25 вопросов. Студент пришел на экзамен, зная 20. Какова вероятность того, что студент ответит на все три вопроса билета?

Пусть события: А – студент знает первый вопрос; В – студент знает второй вопрос; С – студент знает третий вопрос.

Тогда нужная вероятность будет

P( ABC) = P( A)P(B / A)P(C.AB) = 2025 1924 1823 = 11557 .

3. В урну, содержащую два шара, опущен белый шар, после чего из нее наудачу извлечен один шар. Найти вероятность того, ч то извлеченный шар окажется белым, если равно возможны все предположения о первоначальном

P( A/ B3 ) =1. Тогда по формуле полной вероятности

P( A) = P(B1 )P( A/ B1 ) + P(B2 )P( A/ B2 ) + P(B3 )P( A/ B3 ) =

=13 13 + 13 23 + 13 1 = 23 .

4.В пирамиде 5 винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с прицелом, равна 0,95, для винтовки без прицела соответствующая вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок делает один выстрел из произвольной винтовки.

Пусть А – мишень поражена; В1 – произведен выстрел из винтовки с

попадания при первом выстреле р1=0,3, при втором р2=0,6, при третьем р3=0,8. При одном попадании вероятность поражения цели r1=0,4, при двух попаданиях r2=0,7, при трех попаданиях r3=1. Определить вероятность поражения цели при трех выстрелах.

Рассмотрим полную группу несовместных событий: В1 – было одно попадание; В2 – было два попадания;

В3 – было три попадания; В4 – не было ни одного попадания.

Определим вероятность каждого события. По теоремам умножения и сложения вероятностей будем иметь

P(B1 ) = p1 (1 − p2 )(1 − p3 ) +(1 − p1 ) p2 (1 − p3 ) +(1 − p1 )(1 − p2 ) p3 = 0,332 .

P(B2 ) = p1 p2 (1 − p3 ) + p1 (1 − p2 ) p3 +(1 − p1 ) p2 p3 = 0,468 .

P(B3 ) = p1 p2 p3 = 0,144 .

P(B4 ) = (1 − p1 )(1 − p2 )(1 − p3 ) = 0,056 .

Пусть событие А – цель поражена. Выпишем условные вероятности поражения цели при осуществлении каждого из событий В1, В2, В3, и В4.

P( A/ B1 ) = 0,4 , P( A/ B2 ) = 0,7 , P( A/ B3 ) =1, P( A/ B4 ) = 0 .

Тогда по формуле полной вероятности

P( A) = P(B1 )P( A/ B1 ) + P(B2 )P( A/ B2 ) + P(B3 )P( A/ B3 ) + P(B4 )P( A/ B4 ) = 0,6044

Формула Байеса

Вновь рассмотрим полную группу несовместных событий В1, В2,…Вn вероятности появления которых P(B1 ) , P(B2 ) ,…, P(Bn ) . Событие А может

произойти только вместе с каким-либо из событий В1, В2,…Вn, которые будем называть гипотезами. Тогда по формуле полной вероятности

P( A) = P(B1 )P( A/ B1 ) + P(B2 )P( A/ B2 ) +... + P(Bn )P( A/ Bn ) .

Если событие А произошло, то это может изменить вероятности гипотез P(B1 ) , P(B2 ) ,…, P(Bn ) . По теореме умножения вероятностей

P( AB1 ) = P(B1 )P( A/ B1 ) = P( A)P(B1 / A) ,

откуда

Полученная формула называется формулой Байеса. Здесь Р(А) определяется формулой полной вероятности.

Примеры. 1. 30% приборов собирает специалист высокой квалификации и 70% специалист средней квалификации. Надежность работы прибора, собранного специалистом высокой квалификации, 0,9, надежность прибора, собранного специалистом средней квалификации, 0,8. Взятый прибор оказался надежным. Определить вероятность того, что он собран специалистом высокой квалификации.

Событие А – безотказная работа прибора; В1 – прибор собран специалистом высокой квалификации;

В2 – прибор собран специалистом средней квалификации.

Выпишем вероятности гипотез: P(B1 ) = 0,3, P(B2 ) = 0,7 .

2. Батарея из трех орудий произвела залп, причем два снаряда попали в цель. Найти вероятность того, что первое орудие попало, если вероятности попадания в цель каждым из орудий равны р1=0,4, р2=0,3, р3=0,5.

Формула Бернулли

Если производится n независимых испытаний, в каждом из которых вероятность появления события А одна и та же и равна р, то вероятность того, что событие А появится в этих n испытаниях k раз, выражается формулой

В частности, отсюда Рn(0)=qn, Рn(1)=npqn-1, … , Рn(n)=pn.

Примеры. 1. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.

2. Определить вероятность того, что в семье, имеющей 5 деталей, будет не больше трех девочек. Вероятности рождения мальчика и девочки предпо-

Формула Пуассона

При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно, например, 0,951000 вычислить трудно. В этом случае для вычисления вероятности того, что в n испытаниях (n – велико) событие произойдет k раз используют формулу Пуассона

Pn (k) = λkk! e−λ ,

где λ=np=const – среднее число появлений события в n испытаниях. Примеры. 1. Устройство состоит из 1000 элементов, работающих неза-

висимо один от другого. Вероятность отказа любого элемента в течении времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.

2. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути 0,004. Найти вероятность того, что в пути повреждено меньше трех изделий.

n=500, p=0,004, λ=2.

По теореме сложения вероятностей

P = P500 (0) + P500 (1) + P500 (2) = e−2 +12! e−2 + 24! e−2 = 5e−2 = 0,68 .

3. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятность того, что магазин получит более двух разбитых бутылок.

λ=np=1000·0,003=3

P1000 (k > 2) =1 − P1000 (k ≤ 2) =1 −(P1000 (0) + P1000 (1) + P1000 (2))=

=1 −(e−3 +3e−3 +4,5e−3 )= 0,5678 .

Случайные величины

Случайной называется величина, которая в результате испытания принимает одно и только одно возможное значение, какое именно заранее неизвестно.

Случайные величины делятся на дискретные и непрерывные. Случайная величина называется дискретной, если в результате испыта-

ния она принимает одно из значений х1, х2, … , хn, … с соответствующей ве-

роятностью р1, р2, … , рn, …

Непрерывной называется случайная величина, которая может принимать любое значение из некоторого промежутка.

Например, число студентов на лекции – дискретная случайная величина, продолжительность лекции – непрерывная.

Закон распределения дискретной случайной величины

Соответствие между возможными значениями хk случайной величины Х и их вероятностями рk называется законом распределения вероятностей дис-

То, что случайная величина Х принимает одно из значений х1, х2, … , хn,

n

есть достоверное событие и поэтому должно выполняться равенство ∑pk =1

k =1

∞

(в случае бесконечной последовательности значений ∑pk =1).

k =1

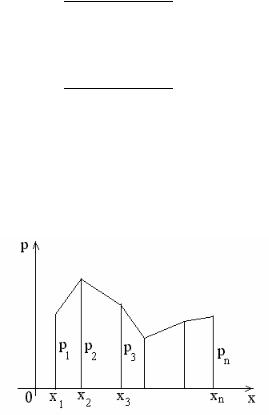
Закон распределения может быть задан графически в виде многоугольника распределения вероятностей, т.е. в виде ломаной, соединяющей точки (хk, рk).

Примеры. 1. Переменная величина Х есть число очков, выпадающее на верхней грани игральной кости при ее однократном бросании. Составить закон

распределения этой случайной величины.

Так как любое число очков при однократном бросании кости выпадает с вероятностью P = 16 , то закон распределения случайной величины имеет вид:

2. Вероятность попадания при каждом выстреле р=0,8. Имеется три снаряда. Определить вероятность того, что будет израсходован один снаряд, два снаряда, три снаряда, если стрельба ведется до первого попадания или промаха всеми тремя снарядами. Составить таблицу распределения случайной величины Х – числа израсходованных снарядов.

Пусть Х – число израсходованных снарядов. Обозначим P( X = xk ) - ве-

роятность того, что будет израсходовано хk снарядов. Тогда

Р(х=1)=0,8, Р(х=2)=(1-р)р=0,16, Р(х=3)=(1-р)2=0,04.

Таблица распределения будет иметь вид

3. Экзаменатор задал студенту 4 дополнительных вопроса. Вероятность того, что студент ответит на любой заданный вопрос 0,9. Составить закон распределения случайной величины Х – числа ответов на заданные вопросы.

Числовые характеристики дискретной случайной величины

Пусть имеем дискретную случайную величину Х с законом распределе-

ния

Математическим ожиданием дискретной случайной величины Х называется сумма произведений всех ее возможных значений на их вероятности

n

M [ X ] = x1 p1 + x2 p2 +... + xn pn = ∑xk pk .

k =1

∞

Для бесконечной случайной величины: M [ X ] = ∑xk pk .

k =1

Можно показать, что при большом числе испытаний среднее арифметическое наблюдаемых значений близко к ее математическому ожиданию.

Математическое ожидание случайной величины Х называется центром распределения вероятностей случайной величины.

Математическое ожидание обладает следующими свойствами.

1.M[C]=C, где С=const.

2.M[CX]=C·M[X].

Характеристиками рассеивания возможных значений случайной величины вокруг математического ожидания служат, в частности, дисперсия и среднеквадратичное отклонение.

Дисперсией случайной величины Х называют математическое ожидание квадрата отклонения значений величины от ее математического ожидания:

Дисперсию удобно вычислять по формуле

D[X]= M[X2] – (M[X])2.

Дисперсия обладает следующими свойствами.

1.D[C]=0, где С=const.

2.D[CX]=C2·D[X].

3. Для независимых случайных величин Х и У D[X+Y]= D[X] + D[Y]. В частности, из свойств дисперсии следует, что

D[С+Х]= D[X]

D[X - Y]= D[X] + D[Y].

Среднеквадратичным отклонением случайной величины называется ко-

Найдем ее математическое ожидание, дисперсию и среднеквадратичное отклонение.

M[X]=2·0,3+3·0,4+4·0,3=3;

D[X]=(2 – 3)2·0,3+(3 – 3)2·0,4+(4 – 3)2·0,3=0,6;

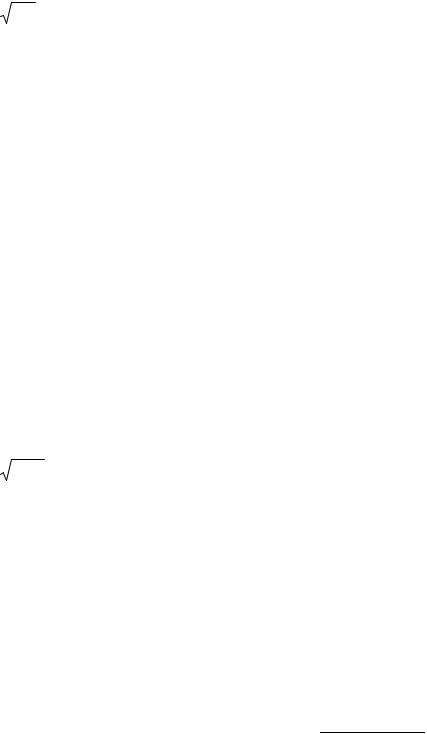
σ[ X ] = 0,6 = 0,77 .

2. В урне 6 белых и 4 черных шара. Из нее три раза подряд извлекают шар, причем каждый раз вынутый шар возвращают в урну. Пусть Х – число извлеченных белых шаров. Составить закон распределения этой величины, определить ее математическое ожидание, дисперсию и среднеквадратичное отклонение.

Вероятность вынуть из урны белый шар р=0,6. Чтобы найти закон распределения случайной величины Х, воспользуемся формулой Бернулли, для

Определим числовые характеристики случайной величины.

M[X]=0,288+0,864+0,648=1,8

D[X]= M[X2] – (M[X])2=1·0,288+4·0,432+9·0,216 – 3,24=0,72. σ[ X ] = 0,72 = 0,85.

Биномиальный закон распределения дискретной случайной величины

Закон распределения дискретной случайной величины Х, которая может принимать n+1 значение 0,1,2,…,n, описываемый формулой Бернулли Pn (k) = Cnk pk qn−k , называется биномиальным. Запишем биномиальный закон в

Определим числовые характеристики биномиального распределения. Пусть Х – число появлений события А в n испытаниях. Если обозначим через Xk – число появлений события А в k-ом испытании, то

Можно показать, что для распределения Пуассона

M[X]= D[X]=λ=np.

Функция распределения непрерывной случайной величины. Плотность распределения

Рассмотрим непрерывную случайную величину Х, заданную а некотором интервале (а, b). Закон распределения вероятностей для такой величины должен позволять находить вероятность попадания ее значения в любой ин-

тервал (х1, х2).

Функция распределения непрерывной случайной величины Х называют функцию F(x), определяющую для каждого значения x (a,b) вероятность

2.F(x) – неубывающая функция, т.е. если х1< х2, то F(x1)≤ F(x2).

3.P(x1 < X < x2 ) = F(x2 ) − F(x1 ) .

4.Р(Х= x1)=0.