Билеты по математической статистике с ответами / Вопросы по ТВиМС [8-14]

8. Выборка из нормального распределения. Представление Хи-квадрат распределения с помощью нормальных. Распределение Стьюдента. Распределение Фишера-Снедекора.

Пусть выборка из N(0, 1).

Введем некоторые распределения , используемые в матстатистике.

Рассмотрим случайную величину . Говорят что имеет -распределение(или распределение Пирсона ) с n степенями свободы. Плотность распределения величины имеет вид

где - гамма – функция Эйлера, определяемая равенством

Семейство -распределение является подмножеством двухпараметрического семейства гамма-распределений Г(b,p), p,b0, с плотностями

При b=1/2, p=n/2, n N. Известное свойство , что сумма двух независимых гамма-распределений Г(b,p) и Г(b,q) снова имеет гамма-распределение Г(b,p+q) , здесь следует непосредственно из представления в виде суммы квадратов незвис нормальных величин.

Пусть сл. в. Y независима от . Рассмотрим случайную вел-ну Распределение величины T_n называется распределением Стьюдента с n степенями свободы. Соответствующая плотность распределения имеет вид

Отметим , что плотность распределения Стьюдента симметрична относительно нуля.

Распределения Фишера-Снедекора F(n₁,n₂) определяется как распределение сл. в. независимы и распределены как и . Плотность распределения Фишера- Снедекора представляется в виде

9. Выборка из нормального распределения. Лемма Фишера.

Лемма: Пусть X₁,X₂,…X_n- выборка из нормального распределения N(a, σ²). Тогда

1) ;

2) и S²– независимы

3) имеет -распределение с (n-1) степенью свободы;

4) имеет распределение Стьюдента с (n-1)степенью свободы.

Доказательство:

1. пусть Y_i=X_i-a распределена по N(0, σ²).

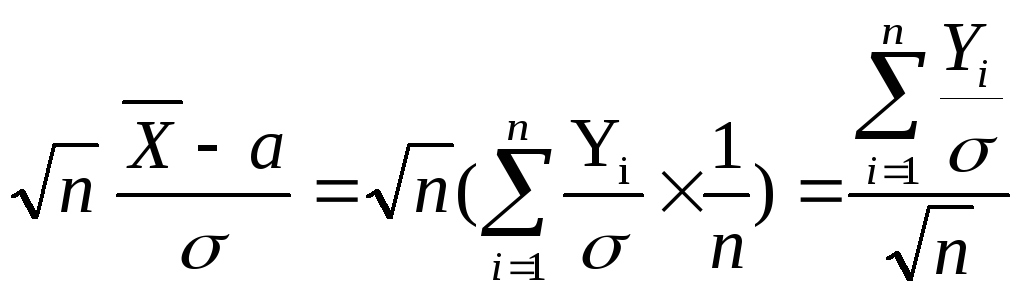, где величина распространена по закону N(0,n), а величина по закону N(0,1).

2. рассмотрим новые величины : , где A- ортогональная матрица , первая строка которой состоит из из чисел равных .

Вычислим матрицу ковариации: отметим что матожидание

Рассмотрим , т.к.

(*)

П.2 cov()

П. 3 следует из представления (*) , т.к. - НОРСВ имеющие нормальное распределение N(0,1).

4) представим

Следствие:

Если X₁…X_n и Y…Y – две независимые нормальные выборки из N(a₁, σ₁₎ и N(a₂ , σ₂), то статистика s₁² / s₂² имеет распределение Фишера – Снедекора.F(n₁ , n₂) .

10. Примеры параметрических семейств распределений.

1) Распределение Бернулли : Bi(1, p)- биномиальное распределение с параметрами 1 и p.

Дискретное распределение , сконцентрированное в точках {0;1} ; P(X₁=1)=p. Параметр θ=p[0;1]

2)Биномиальное распределение

Дискретное распределение, сконцентрированное в точках {0,1…}

P(X₁=k)=C_m^k p^k (1-p)^m-k , k=0,1…m

Параметр θ=(m,p). mN, p[0,1]

3)Семейство распределений Пуассона Pas(λ).

Дискр. распр., неотрицательное, сконцентрированное в точках {0,1…}

P(X=k)= λ^k\(k!)*exp(-λ), k=0,1… θ = λ

4)Геометрическое распр Geom(p)

Дискретное, значения N

P(X₁=k)=p (1-p)^k , k=0,1,… θ =p

5)Нормальное , абсолютно непрерывное распределение N(a, σ²).

p _θ (x)=

Параметр

6) Показательное Exp(α)

Абсолютно непрерывное

Параметр θ = α>0

7)распределение Лапласа L(a,b)

Абсолютно непрерывное

8)Гамма Г(α,p)

Абсолютно непрерывное

11. Постановка задачи точечного оценивания параметра. Функция потерь. Риск.

Пусть ()- статистический эксперимент, результатом которого является набор наблюдений X₁…X_n. Задача точечного оценивания заключается в том, чтобы используя результаты наблюдений, выбрать из множества параметров θ значение, наиболее подходящее в том или ином смысле.

Пусть в качестве оценки параметра θ (или функции от пар-ра g(θ)) выбрана оценка .Для определения близости оценки к истинному значению пар-ра θ вводится функция потерь W(δ, θ) удовлетворяющая следующим условиям:

• неотрицательность W(δ, θ)

• если δ=0, то потери нулевые: W(θ, θ)=0

Наиболее употребительными функциями потерь являются W (δ, θ)=( δ - θ)² - функция потерь Гаусса и W(δ, θ)= |δ - θ| - функция потерь Лапласа.

Функция потерь – величина случайная, зависящая от двух параметров.

Точность оценки измеряется функцией риска R(δ, θ)=E_θ W(δ, θ), где E_θ берется при условии , что распределение соответствует значению параметра θ , т.е. средними потерями при оценивании с помощью δ.

Риск в случае функции потерь Гаусса R(δ, θ)=E_θт.н. средне квадратичное отклонение

Хотелось бы найти оценку , минимизирующую риск при каждом значении θ. Однако в такой постановке задача неразрешима. Действительно, если выбрать в качестве оценки параметра θ некоторое постоянное значение δ = θ₀ , θ₀, то при θ= θ₀ данная оценка абсолютно точна, т.е. имеет нулевой риск. Ясно , что подобная оценка с точки зрения матстатистики абсолютно бесполезна, однако приведённый пример показывает , что , за исключением тривиальных случаев (когда параметр определяется абсолютно точно), оценки , минимизирующей риск при каждом не существует.Для преодоления этой трудности можно ограничить класс рассматриваемых оценок:

• рассматривать только состоятельные оценки

• рассматривать только несмещенные оценки

12)Несмещенное оценивание. Теорема единственности несмещенной оценки с равномерно минимальной дисперсией. Примеры несмещ оценок. Пример параметрического семейства для которого не существует несмещенной оценки.

Оценка параметрической функции называется несмещенной , если при любом значении параметра

или просто

Смещением оценки называется величина .

Отметим что выборочная дисперсия не является несмещенной. С учетом независимости наблюдений (не умаляя общности считаем что ):

Тогда смещение . Нетрудно заметить что несмещенной оценкой дисперсии будет .

Несмещенная оценка не всегда может быть построена.Рассмотрим семейство распределений Пуассона. 1) θ= λ →-несмещенная оценка; 2)если Ограничимся одним наблюдением и построим несмещенную оценку:

, т.е. равенство не достижимо.

несмещенной оценки.

Риск несмещенной оценки совпадает с её дисперсией, поэтому если существует равномерно наилучшая из несмещенных оценок (т.е. имеющая наименьший среди всех несмещенных оценок риск при каждом значении ), то она называется несмещенной с равномерно минимальной дисперсией(НРМД).Т.е.

, где δ^*- несмещ оценка.

Теорема:параметра θ .

Доказательство : пусть существует две - НРМД оценки

Рассмотрим полусумму оценок -несмещ оценка.

Но

Т.о.

. Случайная величина равна нулю.. чтд.

13)Допустимые и недопустимые оценки. Оптимальная, в смысле среднеквадратического риска, оценка дисперсии в классе оценок, пропорциональных выборочной дисперсии и ее смещение.

Какая из оценок лучще: S² или S’²?

.

Найдем наилучшую оценку дисперсии в классе всех оценок вида S²(λ)= λS’², по выборке из нормального распределения N(a, σ²) . Только при λ=1 оценка S(λ) является несмещенной . Вычислим среднеквадратичное отклонение (риск) оценок этого типа

По лемме Фишера

Тогда в итоге получим

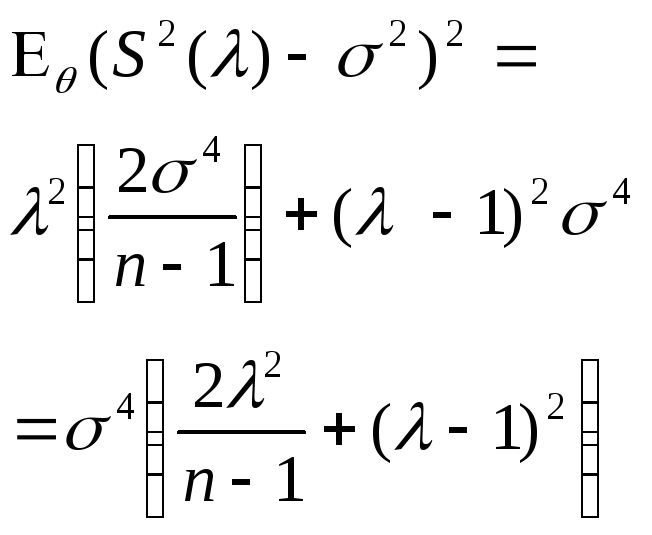
- минимум выражения в скобках достигается при данном значении

-смещенная оценка, наилучшая в данном классе оценок дисперсии нормальной выборки

Оценка называется недопустимой в данном классе если существует оценка такая что

Вывод: Оценка S’² и S² – недопустимые в классе оценок вида (при фиксированном n S₁ лучше S’)

14)Минимаксный и байесовский подходы. Метод построения байесовских оценок. Пример (байесовская оценка среднего нормального распределения с нормальным априорным распределением параметра)

Оценка называется минимаксной если она минимизирует максимальный риск , т.е.

или

Другой подход : Байесовский.

Пусть Q распределение задано на множестве

Байесовским риском оценки , с соответствующим функции потерь W, называется величина

Оценка минимизирующая байесовский риск, называется байесовской.

Пусть на задана (мера) вероятность , плотность которой (относительно доминирующей меры ) задается формулой , где - плотность р-ния θ, а - условная плотность р-ния при условии θ [(- где - мера Лебега)],относительно некоторой доминирующей меры . Байесовский риск(функция потерь Гаусса)

Найдем минимум этой функции по оценкам . Поскольку , фиксируем X, будем минимизировать интегральное выражение по d

Тогда-байесовская оценка.

Совместная плотность

Условная плотность (апостериорная)

- формула Байеса в непрерывном случае

-апостериорное матожидание при условии .

Пример

Пусть выборка из N(a, σ²), σ² –известно; а ~ N()

(σ², -известны, =а- параметр)

Построим байесовскую оценку

Совместная плотность

Т.о плотность можно представить в виде

Фиксируем X, расс-м апостериорную пл-ть

Условное матожидание

- байесовская оценка для функции потерь Гаусса. При больших n эта оценка близка к выборочному среднему . - хорошая (состоятельная ) оценка , если имеет нормальное распределение.