Билеты по математической статистике с ответами / Вопросы по ТВиМС (39-45)

39. Различные постановки задач проверки статистических гипотез. Задачи проверки согласия, однородности, независимости, случайности. Основной метод построения критериев значимости. Альтернативы и различимость.

При анализе различных типов данных возможны различные постановки задач.

Проверка согласия.

Тип данных:

а) однородные – выборка

б) неоднородные – со связями (регрессионная модель)

Гипотеза согласия:

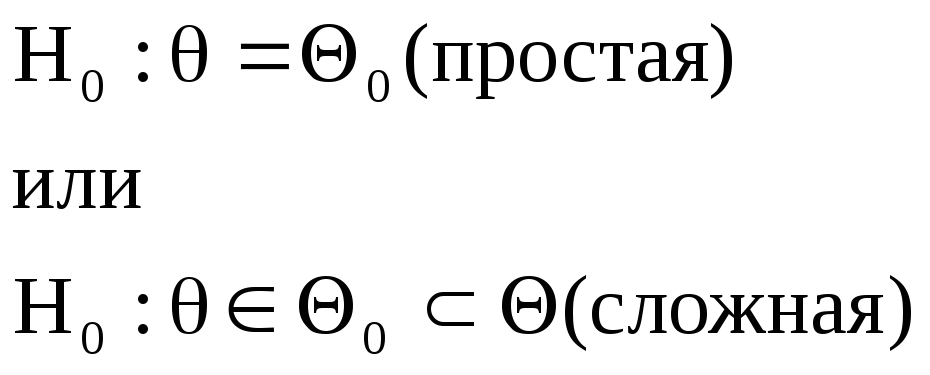
Задача проверки гипотезы согласия в указанной модели – задача проверки согласия (обычно используется ранговый критерий)

Проверка однородности:

Тип данных :

Две (несколько) выборок ~F, ~G

() – независимы

Гипотеза однородности:

(т.е. X₁ и Y₁ имеют одинаковое распределение)

Проверка независимости:

Тип данных:

Выборка из k-мерного распределения с функцией распределения F=F(x₁…x_n), F_i – распределение компонент.

Гипотеза независимости:

- это задача проверки независимости.

Проверка случайности:

х₁,…,х_n – какие-то наблюдения (не обязательно независимые, но обязательно одинаово распределенные)

Гипотеза случайности:

Θ – множество всех распределений

Θ₀ – множество распределений с независимыми и одинаово распределенными компонентами.

Альтернативы и различимость:

Например:

- при альтернативе

Как можно их точно различить?

При фиксированном количестве данных нельзя (!) сказать, что H₀ верна с какой-либо вероятностью (т.к. близкие параметры не различимы). При определенных условиях регулярности граница различимости О(1/)

, n- число данных

Если не рассматривать альтернативу, то критерии, решающие задачи без альтернативы, наз-ся критерий значимости.

Проверка значимости

Ответ: Н₀ отвергается на уровне α либо Данные не противоречат Н₀.

Методы построения критерия значимости

Пусть

- основная гипотеза.

Задача- построить критерий значимости уровня α.

Статистика критерия .

а) - не зависит от параметра при .

б) распределение не зависит от параметра при (если (б) сохраняется и при , то такой критерий бессмысленен).

Распределение известно (напр. ф.р. - G(x)).

Тогда нерандомизованный критерий строиться:

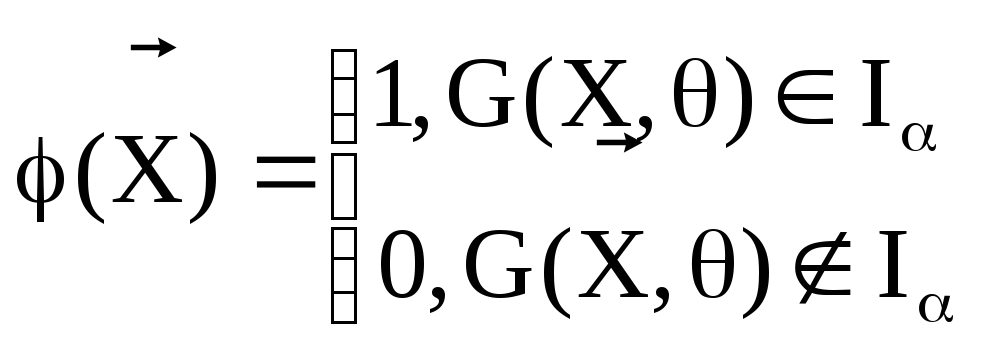
Возможен асимптотический подход.

40. Проверка гипотез о параметрах нормального распределения.

На примере критерия Стьюдента.

1)Данные - выборка из . - неизв.

Задача параметрическая.

Гипотеза: а=а₀ (сложная гипотеза, т.к. σ неизвестно).

Критерий Стьюдента:

Статистика критерия .

- не зависит от мешающего параметра.

При θ= (Н₀)

- не зависит от θ.

Распределение ~S_n-1

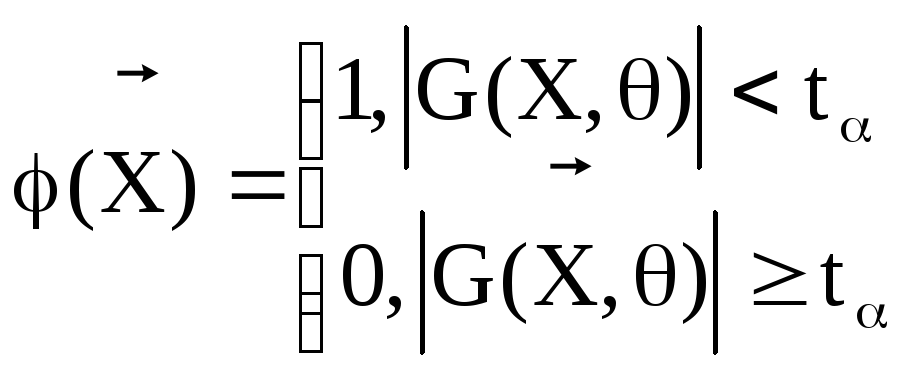
Распределение Стьюдента симметрично

Принимаем гипотезу, если она попала в интервал (<t_α), иначе отвергаем.

2) 2 выборки. По двум выборкам обычно выбирается с одинаковыми дисперсиями. Надо построить статистику для проверки гипотезы однородности.

.

41. Критерий согласия Колмогорова.

Пусть х₁…х_n – выборка из непрерывного распределения в ф.р. F – полностью неизв. F₀ – фиксированная ф.р.

(простая гипотеза согласия, но не параметрическая, т.к. ф-я многомерная).

Критерий Колмогорова:

Статистика критерия: , F_n(x) – выборочная (эмпирическая) ф.р.

Асимптотический критерий , , К – ф.р. Колмогорова.

Для вычисления D_n достаточно вычислить , , , .

Вар.ряд X(1) X(2)

F0(Xi)

|| A

|| B

max(A,B) || C

42. Критерий хи-квадрат для проверки простой гипотезы согласия.

Разбивается вся вещественная прямая на зоны.

Ø, I_i - интервал

Данные группируются (гистограмма)

n_i – число наблюдений в i-й зоне

I_i – зона

Проверка:

H₀ : F=F₀ (простая гипотеза)

n_i можно назвать частотами, n_i – выборочные вероятности .

При справедливости H₀ рассмотрим теоретические вероятности

- теоретические вероятности попадания в зону.

Статистика критерия

Предельное распределение

X

Рассмотрим случайный вектор (n₁…n_r) имеет мультиномиальное распределение

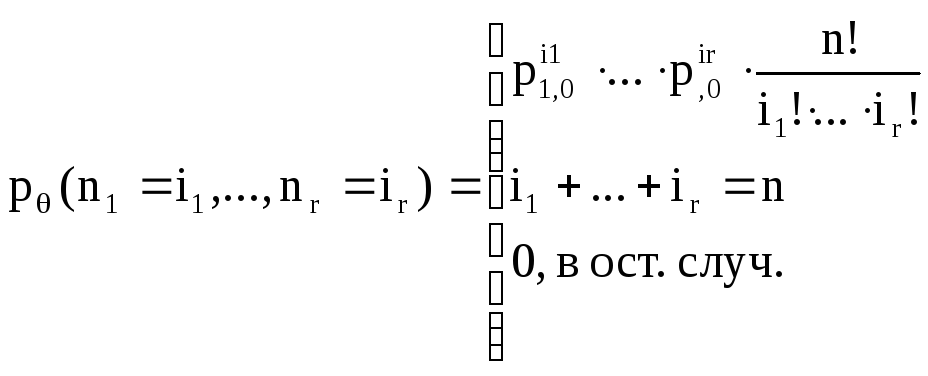
Матрица ковариации

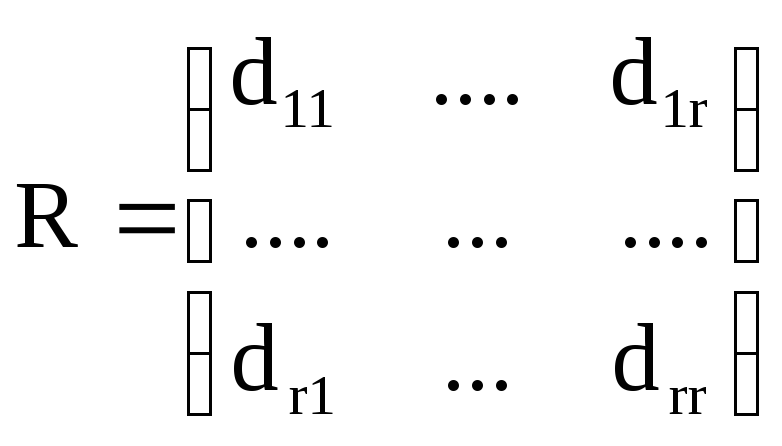
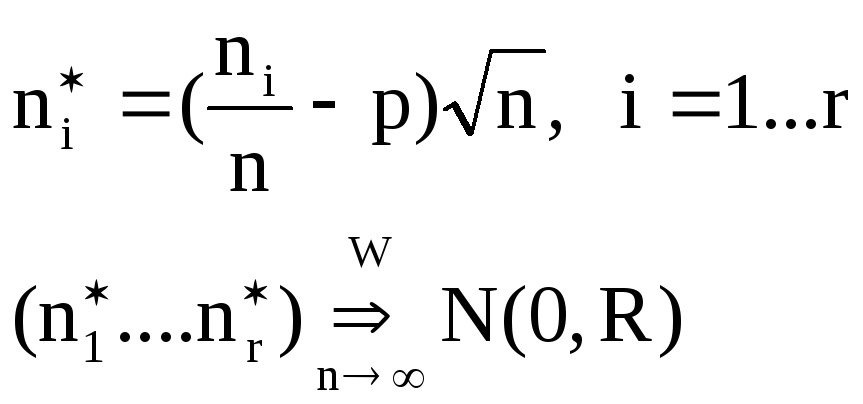
Известно, что, если X~N_k(0,D)

X^TD^-1X~

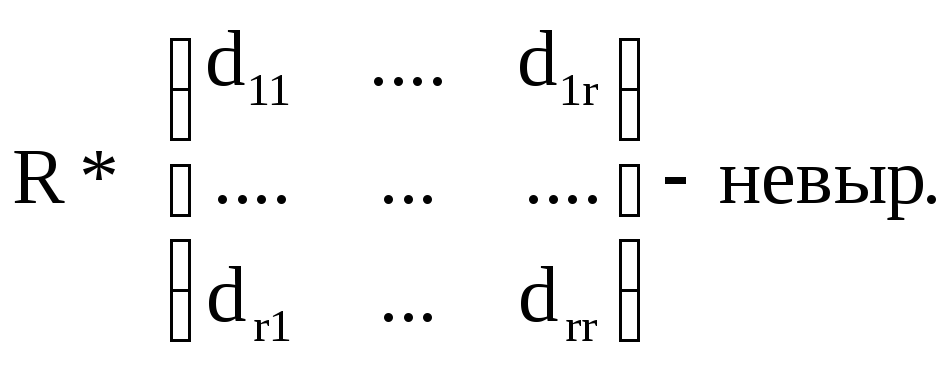
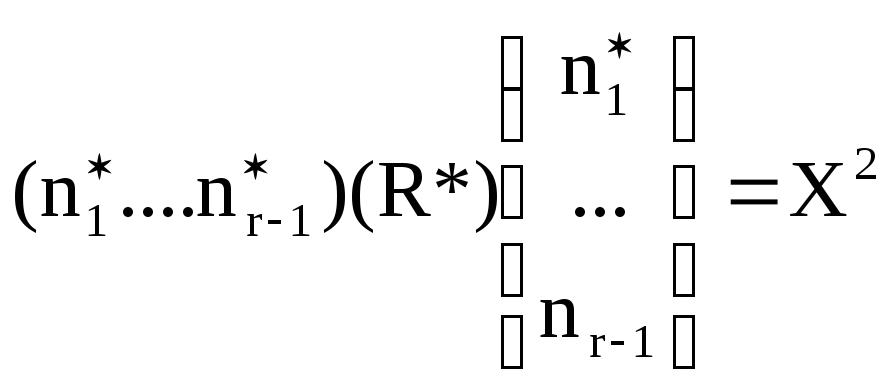
Критерий (ас.)

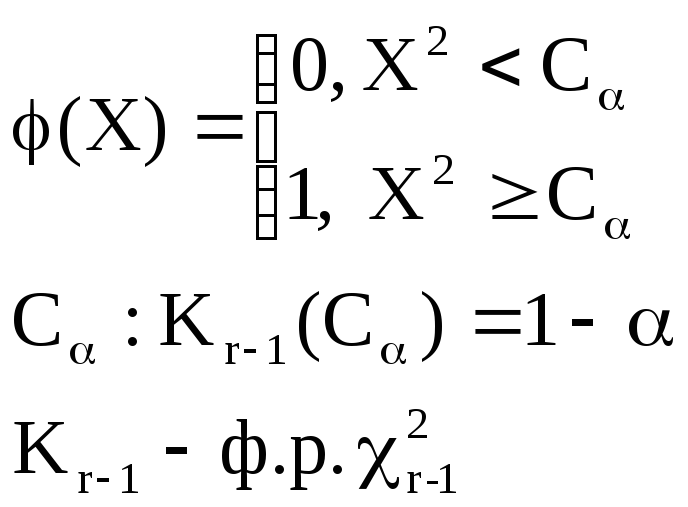
43. Критерий хи-квадрат для проверки сложной параметрической гипотезы согласия.

,,

Например: x₁…x_n~N(a,σ²)

H₀ : a=a₀

dimΘ₀=1

Возможны

H₀ :x₁~N(a,σ²), a,σ² – неизв.

dimΘ₀=2

Поставим задачу проверки значимости

n_i – частоты

p_i(θ) – зависит от θ

-не является статистикой даже при Н₀

I. Мультиномиальное ОМП

n_i~мульт.распр-е (p₁(θ),…, p_n(θ))

Мульт. функция правдоподобия

Если p_i – дифф-мы

Решая это уравнение, получиться оценка (мультиномиальная) ОМП

! Нельзя использовать ОМП по не группированным данным.

Пусть - мультиномиальное ОМП

Выберем статистику

критерия для сложной гипотезы

II.

Утверждение: пусть p(θ) – дважды дифф. по θ.

Матрица имеет ранг m –полный ранг, тогда ~ и

44. Постановка задач линейной регрессии. Метод наименьших квадратов. Геометрическая интерпретация. Оценка по методу наименьших квадратов. Примеры.

Линейная регрессия.

Модель:

Y₁,…,Y_n – независимые (некоррелированные) наблюдения

Пусть предполагается, что справедлива следующая модель .

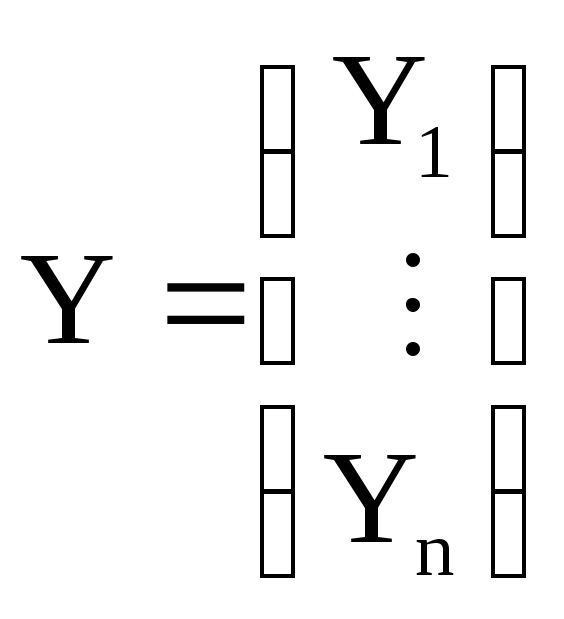- наблюдения (отклики), X’ – n*m –матрица (известны, характеризуют условия проверки эксперимента). Отклики линейно зависят от условий через параметр β. β – неизвестный параметр = . 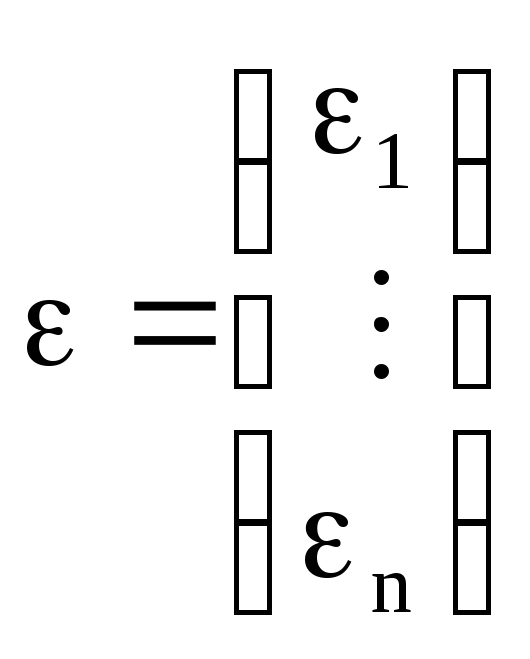-ошибка (шумы).

Основные предположения:

а)

б)

- мешающий параметр – неизвестен.

В условиях (а), (б) EY=X’β.

Задача точечного оценивания – построить оценки параметра β при мешающем параметре .

Оценка по методу наименьших квадратов (МНК)

, где норма

Примеры:

1) Измерительный прибор

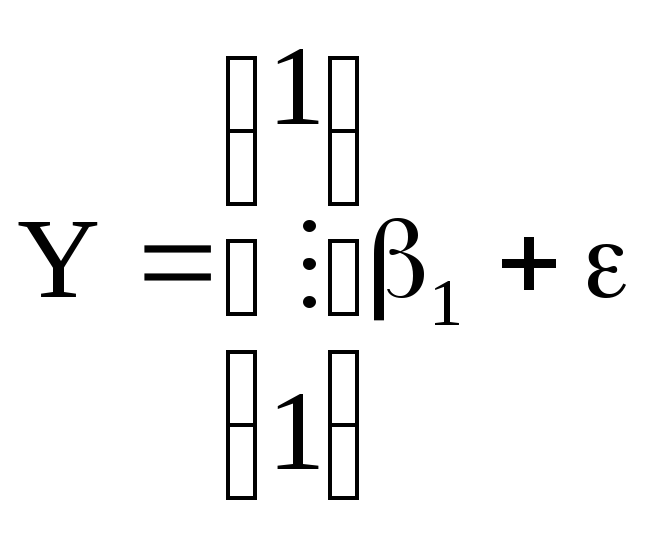/некор. О.Р.С.В./

Прямая на плоскости . - хар-ка процесса.

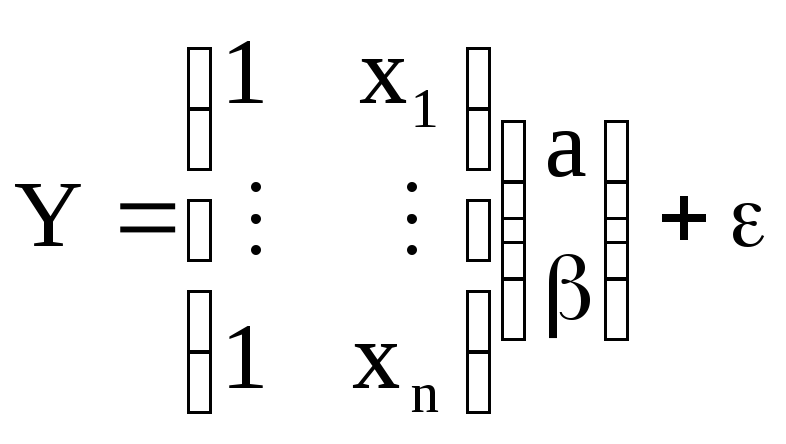
В матричной форме - нормальные уравнения. Если rk(XX^T)=m (т.е. rkX=m), то матрица будет обратимой , получаем -оценка по МНК.

Геометрическая интерпретация:

– i-я строка матрицы X’, то .

_.

_- столбец. -расстояние между элементами Y и X’b.

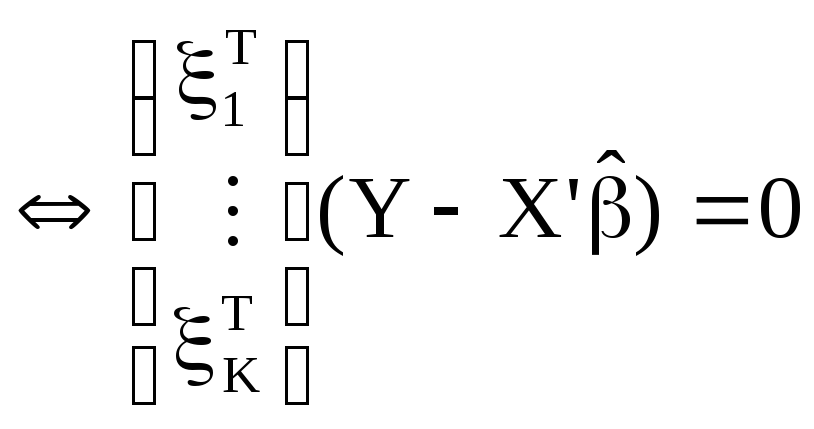
Вывод: решение существует.

45. Функции параметра, допускающие несмещенную оценку (ДНО). Теорема Гаусса-Маркова.

Определение: линейная функция параметра называется ДНО - функцией, если существует такая матрица А – матрица оценки, т.ч. .

Лемма: Сβ – ДНО матрица S: С=SX’

Док-во: Сβ – ДНО , . Ч.т.д.

Теорема (Гаусса-Маркова): Пусть - ДНО – функция. Тогда несмещенная оценка . , т.ч. С=AX’ (т.е. столбцы С – элементы V_m). Данная оценка – оценка по МНК. Пусть - другая лин. несм.оценка, тогда (т.е. - НРМД оценка в классе линейных оценок).

3