Основы дискретной математики (Назарова И.А.)

1. Множество. Операции над множествами. Алгебра множеств.

Множество – объединение в одно целое различимых между собой элементов.

Конечное множество – множество, состоящее из конечного числа элементов.

Бесконечное множество – множество, состоящее из бесконечного числа элементов.

Пустое множество – множество, не содержащее ни одного элемента - 

Универсальное – множество, содержащее все возможные элементы.

О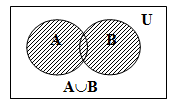 перации над множествами

1) Объединение множеств A и B (A  B) – множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств.

2 ) Пересечение множеств A и B (AB) – множество, состоящее из всех элементов, принадлежащих каждому из этих множеств.

3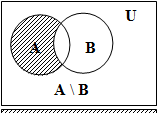 ) Разность множеств A и B (A \ B) – множество, состоящее из всех элементов множества A , не принадлежащих множеству B.

4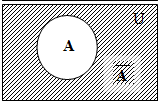 ) Дополнение множества A в универсальном множестве U ( , A) – множество, состоящее из всех элементов универсального множества U, не принадлежащих множеству A.

5 ) Симметрическая разность множеств A и B (AB или AB) – множество, состоящее из всех элементов, принадлежащих в точности одному из этих множеств.A  B = (A \ B)  (B \ A) = (A  B) \ (A  B)

Основные законы алгебры множеств

1) коммутативные законы

А  В = В  А

А  В = В  А

А  В = В  А

2) ассоциативные законы

А  (В  С) = (А  В)  С

А  (В  С) = (А  В)  С

3) дистрибутивные законы

А  (В  С) = (А  В)  (А  С)

А  (В  С) = (А  В)  (А  С)

4) законы с  и u

А   = А А  U = А А  = U

А   =  А  U = U А  = 

=  = U

6) законы идемпотентности

А  А = А А  А = А = А

7) законы поглощения

А  (А  В) = А

А  (  В) = А  В

А  (А  В) = А

А  (  В) = А  В

8) законы Де Моргана

= 

= 

9) законы склеивания

(А  В)  (  В) = В

(А  В)  (  В) = В

2. Бинарные отношения и их свойства.

Бинарное отношение на множествах X и Y – произвольное подмножество прямого произведения двух множеств   Х x Y = {(x,y) | xX, yY}.

Если (x,y), то (x,y) находятся в отношении  или связаны отношением :

х  y или y = (х)

Область определения D бинарного отношения - множество первых элементов каждой упорядоченной пары. D = {x | (x,y)  }

Область значений J бинарного отношения - множество вторых элементов каждой упорядоченной пары. J  = {y | (x, y)  }.

Способы задания отношений

1. список пар

2. характеристическая функция

3. графическое изображение

4. матрица отношения

Свойства бинарных отношений

Пусть  задано на множестве X,   Х2

1) рефлексивность:  х  Х х  х .

2) антирефлексивность:  х  Х х  х.

3) нерефлексивность:  х  Х (x, x)  .

4) симметричность:  х, y  Х х  y => y  х.

5) антисимметричность:  х, y  Х х  y, y  х x = y.

6) транзитивность:  х, y, z  Х х  y, y  z => x  z.

Отношение порядка – антисимметрично, транзитивно.

Отношение нестрого порядка ( ) - рефлексивно, антисимметрично, транзитивно.

Отношение строгого порядка ( ) - антирефлексивно, антисимметрично, транзитивно.

В отношениях полного порядка все элементы сравнимы между собой, а в отношениях частичного порядка не все элементы сравнимы между собой.

Отношение эквивалентности (  ) - рефлексивно, симметрично, транзитивно .

Класс эквивалентности для х : [ x ] = { y Х | x  y }

Обратное отношение получается путём перестановки значений в парах исходного отношения.

Композиция отношений  и  - отношение, состоящее из пар

 ○  = {(x, z)| х  у, y  z }