Медиана распределения

Определяется дискретных случайных величин:

P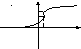(x>)>½

P(x<)<½

_x0

Когда на графике есть ступени ли разрывы, тогда в качестве медианы берется x₀, т.к. скачок участвует и вP(x>) и вP(x<).

Если:

Тогда в качестве медианы можно рассматривать любое значение на этой ступени (чаще всего берут середину ступени).

Пусть теоретической характеристикой является , тогда что собой представляет^*.

Выборочная функция распределения:

Для этого упорядочим выборку в порядке возрастания:

x₁<x₂<…<x_n, те же самые, но в порядке возрастания.

x₁x₂x_n

Возможны 2 случая:

1. Медиана попадает на ступеньку

2. Медиана попадает между ступенек.

Если n– нечетное, то ½ не попадает на ступеньку, тогда в качестве выборочной медианы

^=x_(k+1)чтобы справа и слева было одинаковое число скачков.

Если n=2k, то можно взять любое число из (x_(k),x_(k+1)).

1) Пусть распределение специального вида

Пусть F(x) – равномерное распределение от 0 доb

Выборочный аналог величины b.

b– это крайняя правая точка, аналогb– является максимум.

b^*=x_(n)– максимальное значение выборки.

2) Среднеарифметическое – это оценка Е.

Рассмотрим

^m

m–Eцентр симметрии плотности распределения – это медиана.

Что взять в качестве оценки Е или ?

Пусть мы рассматриваем плотность распределения:

p(x)=- это не нормальное распределение

У нормального распределения быстро убывают концы, E– не существует, поэтому такая оценка неправильна.

Пусть в качестве оценки мы возьмемx.

f(t)=e^itme^-|t| - характеристическая функция

f_x(t)=(e^itm/ne^-|t|/n)ⁿ=e^itme^-|t|=f(t)

т.е. f_x(t) иf(t) для одного наблюдения совпадают, значит совпадаютf_xиf_x. С ростомnизменений не будет, такая оценка очень плоха – никаких приближений к параметру не происходит приn(это объясняет, что Е не существует у такого распределения).

Если взять в качестве оценки m, то получится достаточно неплохой результат.

Гистограмма:

Вместо плотности рассматривается допредельный аналог плотности распределения.

p(x)=F`(x)=

допредельный аналог = гистограмма

n1

n2

nk

i=1,2,…,k

Такая ступенчатая функция называется гистограммой или выборочной плотностью распределения.

Площадь под графиком = 1

ⁿⁱ/_n=1

Теорема:p^*(x)p(x) приn, тогдаmax(h_i) 0 при i<k.

Доказательство:возьмемi

X(a_i,a_i+h_i) – некий интервалi

Введём вспомогательную случайную величину y_i=||_(a,a+h)(x_i),i=1,…,n, тогдаy_i– независимая случайная величина = {1, еслиx_i€ интервалу; 0, в противном случае}

По закону больших чисел ¹/_nⁿ_i=1y_iEy_i=P(x_i(a,a+h))=_a^a+hp(x)dx, тогда

Т.к. h0, то правая часть =p(x)h+0(h), получимч.т.д.

Чаще всего используют гистограмму, когда мало параметров.

14. Оценивание параметров, требования к оценкам, примеры составления несмещенных оценок.

Пусть имеется выборка xс функцией распределенияF(x,). Мы интересуемся, либо, либо функцией=().

Оценкой называется любая функция от выборки, которая не зависит от параметров.

(x₁,…,x_n)=x

Ф(х) – оценка.

Свойства оценок:

Пусть Т=Т(х) = оценка.

1) Оценка Т называется состоятельной, если Т сходится к оцениваемому параметру по вероятность приn:

Tприn

2) Оценка Т называется несмещённой, если мат.ожидание оценки =

E_T=для любых

Для несмещенной оценки среднее арифметическое =0

Для смещенной оценки среднее арифметическое >0

3) Эффективность оценки.

Несмещенная оценка называется эффективной, если она имеет minдисперсию среди всех несмещенных оценок.

Если она не смещенная DT=E(T-)², тогда расстояние между среднеарифметическим и оценкой должно бытьmin.

Теорема:Если Т – несмещенная оценкаиDT0, то Т состоятельная.

Доказательство:Если она несмещенная, тоP(|T-|>)<^DT/^0 по неравенству Чебышева ч.т.д.

Примеры:

1.x– оценкаE

Ex=E(¹/_nⁿ_i=1x_i)=¹/_nⁿ_i=1Ex_i=^mn/_n=m, тогдаxявляется несмещенной оценкой параметраm, она будет состоятельной, когда существуетEX.

Когда существует EX, тоxE(доказано)

¹/_nⁿ_i=1x_imприn, требуется, чтобы существовалоm.

Dx=¹/_n²ⁿ_i=1Dx_i=^DX_i/_n, т.к. всеDx_i– одинаковыDx_i0, если она существует (из предыдущей теоремы она несмещенная и состоятельная).

Оценки эффективные, если выборка из нормального распределения.

2. Оценка дисперсии.

S²=¹/_nⁿ_i=1(x_i-x)²

Является ли она несмещенной?

Можно считать, что Ex_i=0 (т.к. оценкаS²инвариантна относительно сдвига, т.е. если всеx_iзаменить наx_i-Ex, тоS²будет тем же самым). Можно заменить и считать, что Еx_i=0.

S²=¹/_nⁿ_i=1x_i²-x²

ES²=Ex₁²-Ex²=Dx₁-Ex²

Ex²=E(¹/_nⁿ_i=1x_i¹/_nⁿ_i=1x_j)= ¹/_n2ⁿ_i,j=1Ex_ix_j=¹/_n2(ⁿ_i=j=1Ex_i²ⁿ_ij=1Ex_iEx_j=0)=¹/_n2ⁿ_i=1Ex_i²=Dx₁/n, поэтому ES²=DX₁-Ex²=DX₁-Dx₁/n=^(n-1)/_nDX₁

S²– является смещенной оценкой, чтобыS²стала несмещенной, надо рассматривать оценку:S₁²=¹/_n-1ⁿ_i=1(x_i-x)²

15. Метод максимального правдоподобия в оценивании параметров. Пример.

1. Метод моментов.

Пусть теоретическое распределение зависит от .

Пусть -n-мерный параметр.

Можно образовать nвыборочных моментов, например,¹/_nⁿ_j=1x^k_j=S_k,k=1,2,…,m, тогдаS_kEX^k, тогда имеет место примерное равенство

Ex^k=_-^x^kp(x,)dx=m_k(),x– зависит от параметра

Получаем систему из mуравнений

{ S_k=m_k(),k=1,2,…,m

- называется оценкой, полученной по методу моментов. Не очень плохие оценки. В зависимости от параметраF(x,) получается более гибкая оценка, т.к. моменты зависят отm.

2. Метод максимального правдоподобия.

Пусть существует два аквариума.

100 золотых

100 серебренных

Некто вытаскивает рыбку. Он требует ответить из какого она аквариума.

Пусть теперь в первом аквариуме 99 золотых и 1 серебряная, а во втором наоборот.

В этом случае существует возможность ошибиться. Возникает вероятность ошибки.

Если в первом аквариуме 98 и 2, тогда вероятность ошибки еще больше.

Когда число золотых и серебряных рыбок будет одинаково. Вероятность ошибки 50%, при уменьшении золотых рыбок в первом аквариуме, вероятность ошибки будет падать.

Нам надо выбрать 1 из 2-х решений. Наблюдаем событие {1з}.

Вероятность получения золотой рыбки больше, смотря из какого аквариума.

Пусть у нас существует дискретное распределение и x=(x₁,x₂,…,x_n) – случайный вектор, те значения, что мы выбираем.

P(x₁=x₁,x₂=x₂, … ,x_n=x_n)=L()

Выбираем при которой такая вероятность максимальна. Эту вероятность назовем функцией правдоподобияL()

L() – функция правдоподобия.

Метод: Оценка максимального правдоподобия, это есть argmaxL(

argmaxL(

Для непрерывного распределения L(=p(x,)=Пⁿ_i=1p(x_i,).

Мы выбираем , чтобы функция правдоподобия была максимальна.

- состоятельная, асимптотически нормальная, асимптотически несмещенная.

Асимптотически несмещенная – это значит, что 

В этом случае ²– называется асимптотическая дисперсия.

Пример:

1. Пусть существует схема Бернулли. Существует выборка x₁,…,x_n

P(x=1)=p

P(x=0)=q=1-p

Наша задача получить оценку p– роль

Образуем функцию правдоподобия L(p)=p^mq^n-m

Выбираем параметр так, что получаем максимальную функцию.

p=^m/_n

Эта оценка состоятельна и несмещенная.

2. EX– известно и будем оцениватьD

Выборка из нормального распределения.

N(m,²),m– известно

Оценка максимального правдоподобия для D.

Функция правдоподобия.

p(x)=,=²

L(=L(²)=

Надо ²выбрать, чтобы функция правдоподобия была максимальна.

Можно показать, что эта функция имеет максимум (минимум иметь не может)

=0

=0

- несмещенная, состоятельная оценка²

3) N(m,²)m,²- неизвестны

=(m,²)

Функцию правдоподобия нужно дифференцировать и по mи по²и решить систему.

)=

Отсюда в качестве оценки максимального правдоподобия m=¹/_nⁿ_i=1x_i=x– состоятельная, несмещённая.

=0

- состоятельная,смещенная оценка, хотя асимптотически не смещенная

4) Пусть существует равномерное распределение

0 b

p(x)={¹/_b,x(0,b); 0,x(0,b)}=¹/_b||_(0,b)(x)

L(b)=¹/_bⁿПⁿ_i=1||_(0,b)(x_i)=1, когда всеx_i(0,b)

L(b)=¹/_bⁿПⁿ_i=1||_(0,b)(x_i)= ¹/_bⁿ ||_(0,b)(x_max)

Пример:

x(t)=at+b+

x_i=at_i+b+_ii=1,2…n

 - погрешности; t– момент времени, в который происходит измерение.

_iN(0,^)

Неизвестны коэффициенты линейной зависимости.

Нормальная случайная величина p_i(x)=

L(a,b)=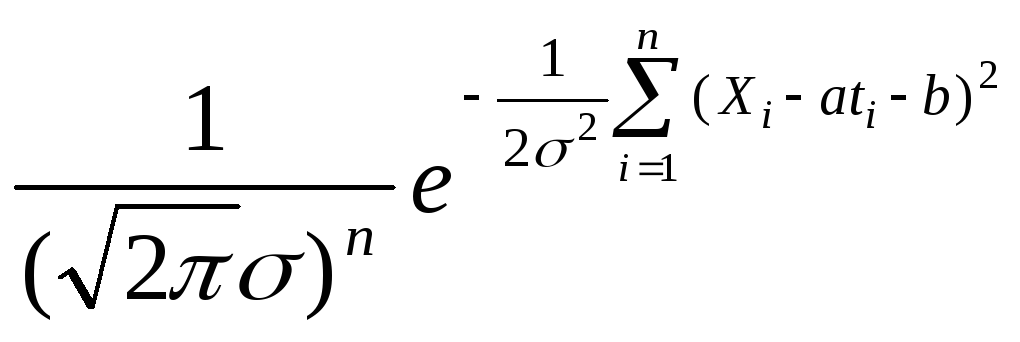

min = - ?

/a =-2t_i=0

/b =-2=0

x=¹/_n

t=¹/_n, xt = ¹/_n

t

xt-xt-at²+ at ²=0

,

Здесь метод максимального правдоподобия совпадает с методом наименьших квадратов.

Оценки являются асимптотически нормальными и их можно сравнивать между собой.

16. Доверительный интервал. Примеры.

Пусть есть деталь длиной m.

Измеряем ее nраз, все измерения имеют нормальные погрешности.

x₁,…,x_mN(0,²)

x_i=m+_i

В качестве оценки можно взять x=m+¹/_nⁿ_i=1_i=m+_n

Dx=D_n=^/n

Ex=m

1-- уровень доверия (доверительная вероятность)^m

 - Уровень значимости

Эти величины находятся с помощью таблиц нормального распределения.

Пример:

Считаем, что дисперсия известна.

- это доверительный интервал

Можно добиться того, чтобы длина интервала стала мала – увеличить n.

Длина детали в этом интервале известна, с хорошей вероятностью:

Мы строим доверительный интервал с известной дисперсией:

Пример:

²– неизвестна.

S²=¹/_nⁿ_i=1(x_i-x)²– оценка для выборочной дисперсии (²)

S²– смещенная оценка.

Несмещенная оценка: S²=¹/_n-1ⁿ_i=1(x_i-x)²(нормированная)

Если мат. ожидание известно, то:

- квадрат распределения.

Известно, что в случае S²=¹/_n-1ⁿ_i=1(x_i-x)²

;

Если , тоpимеет распределение Стьюдента, с одной степенью свободы.

T_n-1=- распределение Стьюдента сn-1 степенью свободы.

т.е. существует единственное отличие: надо пользоваться таблицами распределения Стьюдента с n-1 степенью свободы, вместо таблиц нормального распределения.

При данном уровне доверия

P(N(0,1)>^X/₂)=^/₂

P(N(0,1)<^X/₂)=^/₂

Тоже для случая распределения Стьюдента.

Пример:

Выборка из нормального распределения N(m,²)

Интересуемся ², пустьmизвестно.

В качестве основы возьмем случайную величину: ¹/^ⁿ_i=1(x_i-m)²

Она имеет распределение _n²(n– степени свободы)

Для этого распределения существуют таблицы.

_n

Сумма площадей хвостов=

P(¹/^ⁿ_i=1(x_i-m)²>X_/2)=^/₂(1)

P(¹/^ⁿ_i=1(x_i-m)²<Y_/2)=^/₂(2)

Если X_/2,Y_/2подобрать, так что выполняются соотношения (1), (2), то

P(Y_/2<¹/^ⁿ_i=1(x_i-m)²<X_/2)=1-

17. Лемма Неймана Пирсона. Пример критериев, построенных согласно этой Лемме.

x₁,…x_n,p(x,)

Существует гипотеза H₀,H₁

Пусть гипотезы простые.

H₀:=₀p(x,_)=p₀(x)

H₁:=₁ p(x,₁)=p₁(x)

Задача: вычислить, какая из гипотез верна, но можем ошибиться.

Ошибка первого рода: отвергнуть H₀, когда она верна.

Пусть - вероятность ошибки 1-го рода.

Ошибка второго рода: принять H₀, когда она неверна.

Пусть ₁– вероятность ошибки второго рода.

 - уровень значимости <₀, т.е. мы условно минимизируем₁

Лемма Неймана-Пирсона:

Пусть существует выборка X=(x₁,…,x_n)

Плотность выборки p₀(),p₁() – плотности распределения.

H₀;p()=p₀()

H₁;p()=p₁()

Образуем в RⁿобластьD={} - критическая область, критерий проверки гипотезы.

Если D, тоH₀– отвергается.

Если мы используем такой критерий, то вероятность ошибки первого рода фиксирована =_, а вероятность ошибки второго рода минимальна.

Вероятность ошибки первого рода:

=_DP₀()d*

Вероятность ошибки второго рода:

_=_D`P₁()d**

D` - дополениеD

т.е. при условии, что * фиксирован, ** будет минимален при любом критерии.

Замечания:

1. C–const: выполняется=P₀()d{}

С можно однозначно найти по уровню значимости.

2. P()=P(=)

Если распределение дискретно, то всё остаётся справедлим при условии, что Cвыбрано, так, что выполняется.

Пример:N(m,²),^- известно

H₀:m=m₀

H₁: m=m₁

D={:}={:}={:}

={:}={:}

1. Пусть m₁>m₀– поделим наm₁-m₀

D={:}

2) Пусть m₁<m₀, тоD={:}

Алгоритм:

m₁>m₀

p(>C)=p(=

Находим x_

P(N(0,1))>X_)=

=X_

С=

если x>C=> гипотезу отвергаем

Пример:

Выборка из закона Пуассона с неизвестным параметром :

X=(x₁,…,x_n)p(x)=P(X=x)

H₀:p(x)=P₀(x)=_

H₁:p(x)=P₁(x)=_

XDH₀– отвергается.

D:{XRⁿ:}

₀– вероятность ошибки первого рода – уровень значимости

_- вероятность ошибки второго рода

=1-_- мощность критерия

p₁(x)=p(X=x)= x=0,1,2…

p()==

1)_>_

∑X_i>C₂ x>C₃

2)_<_

x<C₃

P₀(x<C₃)=

P₀(ⁿ_i=1x_i<C₂)=

C₂=nC₃

ⁿ_i=1x_i– имеет распределение Пуассона с параметромn

18. Критерий Колмогорова-Смирнова их непараметричность.

Критерий Колмогорова:

Пусть имеется выборка с функцией распределения F(x).

H₀: F(x)=F₀(x)

H₁: F(x)F₀(x)

Выборочная функция распределения:

F_n^*(x)^pF(x)

Расстояние:

(F_n^*,F₀)=nSup_x|F_n^*(x)-F₀(x)|=D_n не зависит отF₀.

F_n^*- теоретическая,F₀ - гипотетическая

Если - маленькая, то беремP(D_n<x)k(x) приn

k(x)=1-^_k=-e^-k2x2- функция распределения Колмогорова.

Можно построить следующий критерий:

D_n>C, тоH₀– отвергается

D_n<C, тоH₀находится в согласии с нашими наблюдениями.

Алгоритм:

1) Фиксируем уровень значимости.

2) По таблице Колмогорова подбираем X_, чтобыP(D_n>X_)=.

Если Н₀верна, то значит произошло очень маловероятное событиеX_,D_n стремится к конечному пределу, а если Н₀неверна, тогда оценкаD_n

Критерий Колмогорова является не параметрическим.

Покажем, что распределение D_nне зависит отF₀(x), если гипотеза верна.

Лемма Смирнова:

1. X– случайная величина сF(x) – непрерывная функция распределения, тогдаY=F(x) имеет равномерное распределение на [0,1]

2. Если Y имеет равномерное распределение на [0,1], тоF^-1(Y) имеет непрерывную функцию распределенияF(X).

Следствие:

Если x₁,…,x_n имеют функцию распределенияF(X), независимые иy₁,…,y_nнезависимые, тогда они имеют стандартное равномерное распределение.

Док-во:

P(Y<x)=P(F(x)<x)=P(X<F^-1(x))=F(F^-1(x))=x

Выборочная функция распределения:

F_n^*(x)=¹/_nⁿ_i=1||_(-,x)(x_i)

sup_x|F_n^*(x)-F(x)|=sup_x|¹/_nⁿ_i=1(||_(-,x)(x_i)-F(x))|=sup_y|¹/_nⁿ_i=1(||_(-,F`(y))(x_i)-F(F^-1(y))|=

sup_y|¹/_nⁿ_i=1(||_(0,y)F(x_i)-y)|=sup_y|¹/_nⁿ_i=1(||_(0,y)(y_i)-y)|

Критерий одинаковый для любого распределения, т.е. не параметрический.

Критерий Колмогорова-Смирнова:

Имеются две выборки:

x₁,…,x_n F(x)

y₁,…,y_mG(x)

F(x) иG(x) неизвестны.

H₀ : F(x)=G(x)

H₁ : F(x)G(x)

Критерий: гипотеза H₀отвергается, еслиD_n,m>C.

19. Критерий ². Примеры.

Есть выборка x₁,…,x_n, разбиваем вещественную прямую на интервалы.

n₁n₂n_k

_₂_k

Критерий:

²=

p_i=P₀(x_i) – нулевая гипотеза

H₀:F(x)=F₀(x)

Если гипотеза верна, то распределение стремится к ²_n-1степенями свободы, если неверна, то².

{²>C} => гипотеза отвергается

p(²_n-1>C)=- пользуемся таблицей распределения для²_n-1степенями свободы.

Пример:

20 лет собирали сведения о количестве кавалеристов, погибших в результате гибели под ними коней; данные были получены по ежегодным докладам 10 полков, всего 200 докладов

Число погибших x	0	1	2	3	4	5	6
Число донесений rx	109	65	22	3	1	0	0
npi (по Пуассону)	108,7	66,3	20,2	4,1	0,6	0,07	0,01

x=x=(165+222+33+41)/200= 0,6%

p_i=^i/_i!e^-

Данные группируют

Число погибших x	0	1	2	>3
Число донесений rx	109	65	22	4
npi (по Пуассону)	108,7	66,3	20,2	4,8

²=0,32

P(_²>t_α)=0,05

t_α=6.

Дополнительный материал:

Пример:

1. Рассмотрим единичный круг. Равномерное распределение.

Совместная плотность распределения точки a=0. Одномерная плотность распределения точки а не равна нулю.

p₁(x)=когдаxнаходится в интервале от [-1;1], еслиx[-1,1], плотность=0

Эта плотность не равна 0, по оси yтоже плотность не равна 0 => у[-1,1], т.е. одномерные плотность не равны, а совместная плотность равна 0, т.е. координаты этого вектора зависимы.

Получение одномерной плотности распределения из двумерной:

Пусть есть вектор (x,y) с плотностьюp(x,y), тогда плотность компонентыx:

p(x)=.

Пусть F₁(x₁) – функция распределения случайной величиныF₁(x₁)=P(X<x₁)=_x<x1p(x,y)dxdy=

Функцию распределения продифференцируем.

P₁(x₁)=(F₁(x₁))`=.

Замечание:эта формула верна и для любого числа компонентов. Если мы имеемp(x₁,…,x_n) и по каким-то компонентам, мы проинтегрируем, от интеграла получим плотность распределения другого случайного вектора, который получится вычеркиваем из исходного тех компонент по которым мы проинтегрируем.

Теорема Эссена(для примера без доказательства):

Пусть существует последовательность независимых случайных величин, они могут иметь разное распределение x₁,…,x_n, рассматривается сумма этих величин:

S_n=ⁿ_i=1x_i

Вводится обозначение:

В_n=DS_n=ⁿ_i=1Dx_iиm_n=ES_n=ⁿ_i=1Ex_i

L_n=

Имеет место неравенство: sup|L_n

C– некая постоянная величина

Т.о. если L_n0, тогда нормированная сумма независимых случайных величин равномерно сходится к нормальному распределению.

Частный случай:

Если E|x_i|³<A,Ex_i²>k, тогдаB_n>kn

L_n<, стремится к 0 со скоростьюn

Лемма:

Пусть функция F(x) непрерывна, последовательностьF_n(x)F(x) для любогоx,

отсюда sup|F_n(x)-F(x)|0

Доказательство:

1. Пусть существует плоскость, на которой присутствует функция распределения.

Разобъем ось у.

Пусть >0,aразбиение такое, что 0<y_i+1-y_i<.

Пусть x_k– такая точка, чтоF(x_k)=y_k– т.к.F(x) – непрерывна, то такое распределение всегда найдется.

2. Покажем, как связаны 0<F_n(x_k+1)-F_n(x_k)<|F_n(x_k+1)-F(x_k+1)|+F(x_k+1)-F(x_k)

|F(x_k)-F_n(x_k)|<3

можно представить, что nтакое большое, что каждое из 3-xслагаемых не превосходит.

3. Для любого x, найдется такоеk, чтоx_k-1<x<x_kи рассмотрим |F_n(x)-F(x)|:

|F_n(x)-F(x)|<|F_n(x)-F_n(x_k)|+|F_n(x_k)-F(x_k)|+|F(x_k)-F(x)|<F_n(x_k+1)-F_n(x_k)++F(x_k)-F(x_k-1), т.к.F_n(x) – возрастает, то |F_n(x)-F_n(x_k)|<F_n(x_k+1)-F_n(x_k), т.к.F_nсходится кFв каждой точке, то |F_n(x_k)-F(x_k)|<вместо |F_n(x)-F(x)|<3++=5

x_k-1<x<x_k

|F_n(x)-F(x)|<5мы доказали равномерную сходимость, ч.т.д.

Семейство нормальных распределений.

Пусть существует стандартное нормальное одномерное распределение

гдеX- нормальная стандартная случайная величина.

Если гдеX- нормальная стандартная случайная величина, тоY– будет нормальной случайной величиной.

Характерная функция стандартного нормального распределения , тогда

Нам удобно, что семейство распределения было задано относительно предела случайных величин.

Если , то и распределения сходятся – замкнутость относительно предельных переходов

Если , тогда- это есть константа случайной величиныY.

Y=b

Вырожденные, нормальные случайные величины, у которых дисперсия = 0 – это постоянная и EX= этойconst.

Свойство: семейство нормальных распределений замкнуто относительно предельных переходов и линейных преобразований.

Если Y=aX+b,X-нормальное, тоY- нормальное.

Нормальное распределение замкнуто относительно сложения нормальных независимых величин: если X,Yнормальные независимые, тогдаX+Yнормальные.

Нормальное распределение полностью определяется, гдеэтоEX, аэтоDX, можно вычислять плотность распределения,производя линейные преобразования случайных величин.

Пусть ,-независимые, то чтобы найти плотность распределенияY,достаточно определить параметры для случайной величиныY:

зная характеристики иможно определить,.

Пример:

Пусть Xимеет нормальное распределение с параметрами 1,1:- обозначает мат ожидание и дисперсию.

Пусть имеет

Найти:

1. Написать плотность распределения

2. Написать плотность распределения

Формула преобразованной случайной величины

Семейство многомерных нормальных распределений.

X– стандартный нормальный вектор, у каждого компонента существует нормальное распределение.

в качестве нормальной величеныстандартная нормальная (1)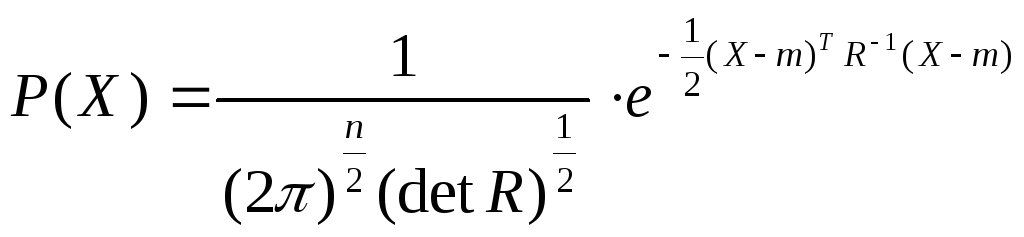

- ковариационная матрица

- вектор математического ожидания

Особенность: Если - вырождена, тогда- не существует и.

Формула не применима.

Надо переходить к приделу, мы не всегда получаем const.

Если матрица имеет, то распределение сосредоточено в-мерном подпространстве исходного- мерного пространства, т.е. существует переменные лишние.

Существует замкнутость относительно предельных переходов.

(1)говорит, что существует замкнутость относительно линейных преобразований.

Существует замкнутость относительно сложения независимых нормальных случайных величин.

! Компоненты нормального вектора – нормальны. Кроме того, пусть существует- нормальный вектор:

разобьем его на дваи на, то два последних под вектора будут нормальными.

Упражнение: Для двумерного нормального распределения

- нормальное

- дисперсия

-коэффициент корреляции.

Следствие из формулы:ЕслиX,Y– нормальные, то из равенстваследует независимость компонент. Совместная плотность распределения распадается в произведение – а это независимость компонент.

Если существует мерный вектор- нормальный.

это означает независимость компонент, еслитои- независимы.

Независимость и некорреляционность - одно и тоже для нормальных векторов.

Т.е. если X,Y–нормальные и, то- тоже нормальный, его распределение можно рассчитать (учитывая, что X,Y– зависимы)

Момент нормального распределения.

Пусть X–случайная величина имеет

?

Возьмем характеристическую функцию

ряд Тейлора ряд Тейлора.

по формуле:

В частности

Семейство биномиальных распределений.

,

- обозначение семейства.

Семейство распределений Пуассона.

-обозначение семейства.

- сумма независимых случайных величин.

- независимая величина с распределением Пуассона с параметром, тогдаX– случайная величина с параметромn.

Асимптотическая нормальность выборочной медианы.

n=2k+1

X₍₁₎<X₍₂₎<…<X_(2k+1)

X_(k+1)=

p(x)=C_2k+1^k,1,kF^k(x)(1-F(x))^kp(x)=(2k+1)!/k!²F^k(x)(1-F(x))^kp(x)

Y=(2k+1) (X_(k)-) - будем доказывать асимптотическую нормальность этой медианы

F(M)=½

P_y(y)=**

n!nⁿe^-n

*=

==

=

Доказали, что выборочная медиана асимптотически нормальная/

x₍₁₎<…<x_(k+1)<…<x_(2k+1)

x_(k+1)=- выборочная медиана

n(x_(k+1)-),

Рассмотрим пример, когда для оценки первого параметра существует 2 оценки

Если распределение симметрично, то медиана = мат.ожиданию

Какая из этих оценок лучше?

Определяется по дисперсии

^m=

Медиана имеет только асимпототическую дисперсию

Dx=^/n

Дисперсия выборочной медианы:

D=

p(x)=

D=- хуже дисперсия.

Если мы сомневаемся в нормальном распределении, то лучше выборочная медиана.