Шпаргалка по теории вероятности

1.

Классическое определение вероятности.

Имеется конечное число равновероятных событий (исходов) – ω₁ ω₂ …. ω_n

Любое множество элементарных исходов называется событие: A, B, C…

Вероятность события А : p(A)=n(A)/n , где n(A) – число элемент. исходов, входящих в А.

Геометрическое определение вероятности.

А – событие.

А  A'

A' – множество, сопоставленное событию А

Для А' определена мера μ(А') (длина, площадь)

Ω – достоверное событие

Ω  Ω' ; μ(Ω')

Вероятность события А : p(A)= μ(А') / μ(Ω')

3.

Парадокс Бертрана.

При различных сопоставлениях событию А множества А' получается различный ответ в решении задачи.

Задача. Имеется круг. В нем выбирается хорда. Определить вероятность того, что длина хорды будет больше длины стороны правильного треугольника, вписанного в этот круг.

Решение 1.

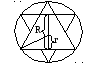Все хорды перпендикулярны фиксированному диаметру. Тогда имеется соответствие между хордами и точками на диаметре – точки пересечения. Впишем 2 правильных треугольника . Все хорды большие его стороны лежат между треугольниками. P =r/R=1/2

Решение 2.

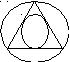Каждая хорда круга однозначно определяется координатой е середины. Ч/з каждую точку круга можно провести только одну хорду, которая будет больше стороны треугольника. P=r² / R² =1/4

Решение 3.

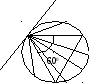Можно рассматривать те хорды, у которых закреплен один из концов. P=60/180 = 1/3

4,

Аксиоматика Колмогорова.

Пусть F - некоторая система подмножеств множества элементарных событий Ω, F={A, B, …}, A CΩ , B CΩ, … Множество F называется алгеброй (σ-алгеброй), если выполнены следующие условия:

1. Ω € F

2. Если А € F, то Ā € F. (Ā – дополнительное событие к А, заключ. в том, что А не произошло)

3. Если А € F и B € F, то А U B € F и А ∩ B € F.

P- вероятностное распределение на σ-алгебре (алгебре F). P(A) – вероятность события А, где А € F. Выполнены следующие аксиомы:

1. P(Ω)=1

2. 0<=P(A)<=1.

3. Если A,B € F и A∩B=0, то P(AUB)=P(A)+P(B)

Сумма А+В (AUB) – называется такое событие, которое состоит в том, что либо произошло А, либо В, либо оба.

Из А следует В (А=> B) если событие А может произойти только с В.

Дополнение (отрицание) к событию А – Ā, называется событие, которое состоит в том, что А не произошло.

Разности событий А\В называется такое событие, которое состоит в том, что А произошло, а В не произошло.

5.

Свойства вероятности.

1. P(Ø)=0

2. P(Ā)=1-P(A)

3. A(B, то P(A)<P(B)

4. 0<=P(A)<=1

5. Непрерывность вероятности

А) А₁C=A₂C=….C=A_nC=…… A=U^∞_n=1A_n => lim_n∞ P(A_n)=P(A)

B) B₁)=B₂)=….)=B_n)=…… B=∩^∞_n=1B_n => lim_n∞ P(B_n)=P(B)

6.

Теорема сложения вероятностей.

P(AUB) = P(A)+P(B)-P(AB)

Обобщенная теорема сложения вероятностей.

События А,В,С

P(AUBUC)=P(A)+P(B)+P(C)-P(AB)-P(BC)-P(AC)+P(ABC)

P(A₁UA₂U…UA_n)=ΣP(A_i) – Σ_i≠j P(A_iA_j) + Σ_i≠j≠kP(A_iA_jA_k) - ……(-1)ⁿ⁺¹ P(A₁…A_n)

Задача о рассеянной секретарше.

Секретарше надо разослать n писем. Она разложила письма в конверты и заклеила их, не надписав адреса. Событие А заключается в том, что хотя бы один адресат получит свое письмо. А_i – i – й адресат получит адресованное ему письмо.

А=UA_i

P(A_i)=1/n

P(A_iA_j)=1/((n-1)n) => P(A)=1-1/(n(n-1))*C_n²+……=1-1/2!+1/3!-1/4!+…+(-1)ⁿ⁺¹*1/n!=1-1/e

7.

Условная вероятность.

Имеется 2 события А и В. P(A/B)=P(AB)/P(B). А произошло при условии, что произошло В.

Теорема умножения (из определения условной вероятности).

P(AB)=P(A/B)*P(B)

P(ABC)=P(A/BC)*P(BC)=P(A/BC)*P(B/C)*P(C)

8.

Независимость событий.

А не зависти от В, если P(A/B)=P(A)

B не зависти от A, если P(B/A)=P(B)

P(A/B)/P(B)=P(A), P(B)≠0

P(B/A)/P(A)=P(B), P(A)≠0

Если А не зависит от В, то и В не зависит от А.

А и В называются независимыми, если P(AB)=P(A)*P(B)

Событие, имеющее вероятность =0 не зависит от любого события.

События A,B,C: P(AB)=P(A)*P(B)

P(AC)=P(A)*P(C) P(ABC)=P(A)*P(B)*P(C)

P(CB)=P(C)*P(B)

Если А и В независимы, то Ā и В тоже независимы. P(ĀB)=P(Ā)*P(B)

9.

Формула полной вероятности.

Событие А

Гипотезы – Н₁……Н_n: 1. H_i ∩ H_j =0 при j≠i ; 2. A C UH_i ;

Формула полной вероятности P(A)=Σ P(A/H_i)*P(H_i)

10.

Формула Байеса.

Событие А

Гипотезы – Н₁……Н_n: 1. H_i ∩ H_j =0 при j≠i ; 2. A C UH_i ;

P(H_j/A) = P(A/H_j)*P(H_j) / P(A)= P(A/H_j)*P(H_j) / (Σ P(A/H_i)*P(H_i))

11.

Схема Бернулли.

Есть n-независимых испытаний. Каждое испытание имеет 2 исхода – успех или неудачу.

Вероятность успеха – p, неудачи – q=1-p

Успех – 1, неудача – 0.

Есть множество Ω.

ω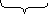={1100…11010} – элементарное отдельное событие.

n

A C=Ω

P(ω)=p^m q^n-m, где m – число успехов (единиц) в ω

P(A)=Σ _ω€A P(ω) (ω€A)

P(Ω)=Σ _ω€A P(ω)=Σ_ω p^m q^n-m= Σⁿ_m=0 C_n^m p^m q^n-m= (p+q)ⁿ=1

P_n(m)= C_n^m p^m q^n-m – вероятность того, что произойдет ровно m успехов.

P_n(n)=pⁿ – все успехи

P_n(0)=qⁿ – все неудачи

P( хотя бы один успех) =1-qⁿ

P( хотя бы одна неудача) =1-pⁿ

Полиномиальная схема.

Имеется последовательность n испытаний. Каждое испытание имеет k исходов (н-р игральная кость)

P_n(m₁…m_k)

Количество исходов m₁- первого типа; m₂ – второго типа и т.д.

m₁+m₂+…+m_k=n

P_n(m₁…m_k) = C_n^m1.m2,..mk p₁^m1 p₂^m2 …p_k^mk

p₁^m1 – вероятность первого исхода и т.д.

C_n^m1.m2,..mk = n!/( m₁!...m_k!) – число способов, с помощью которых можно множество из n элементов разбить на k подмножеств.

P_n(m₁, m₂) – вероятность того, что число успехов находится в интервале (m₁, m₂)

12.

Теорема Пуассона.

P_n(m) - m – фиксировано, n стремится к бесконечности.

Вероятность p имеет порядок 1/n

Последовательность серии испытаний

Е₁: p₁,q₁ – одно испытание

……………….

Е₂: p_n - n испытаний

p_n~λ/n, при λ>0

np_n λ при n∞

Теорема : P_n(m)  λ^m/m!*e^{- λ}, для всех m=0,1,2…

13.

Локальная теорема Муавра – Лапласа.

x=x_n,m=(m-np)/ (√(npq)), m – число успехов.

|x|<C при n∞

√(npq)* P_n(m) ~ 1/(√(2π))*exp(-x_n²/2)

Интегральная теорема Муавра – Лапласа.

x=x_n,m=(m-np)/ (√(npq)) n ∞

P(a<=m<b)≈ Φ((b-np)/ (√(npq))) - Φ((a-np)/ (√(npq)))

Φ(x)=1/(√(2π)) ∫^x_-∞ exp(-t²/2) dt

14.

Случайные величины.

Вероятностное пространство – (Ω, F, P)

Ω – множество элементов (ели оно конечно, то пространство дискретное)

F – событие

P – вероятность

Случайной величиной называется функция, заданная на Ω.

X=X(ω), ωЄ Ω

{ω: X(ω)<a} ЄF для всех а ЄR¹

{ω:X(ω) ЄB} Є F для всех ВЄß

ß - σ-алгебра борелевских множеств – содержит все конечное объединение интервалов (и бесконечные множества)

P(X(ω)) ЄB)

Опр. Рассмотрим μ(В)=P(ω:X(ω) ЄB)

μ(В) – задана на множестве В Є ß

μ(В) – распределение случайной величины Х.

Функция распределения случайной величины.

F(x)=P(X<x)=P (ω:X(ω)<x)

P(a<=X<b)= μ([a,b))= μ(-∞, b) - μ(-∞,a)=F(b)-F(a)

A= U_iЄ(1..n)[a_i,b_i)

P(X ЄA)= μ(U_iЄ(1..n)[a_i,b_i))=Σ _iЄ(1..n) μ([a_i,b_i))= Σ _iЄ(1..n)(P(X<b_i) – P(X<a_i))

Свойства функции распределения.

1. 0<=F(x) <=1

2. F(x) не убывает

3. 1) lim F(x)=1 при x ∞ 2) lim F(x)=0 при x -∞

4. F(x) – непрерывна слева, приближается к х слева

Это полный набор свойств. Если хотя бы одно свойство не выполнено, то это не функция распределения.

15.

Свойства плотностей распределения.

Случайная величина Х имеет дискретное распределение, если ее множество значений конечно.

p(X=x_k)=p(x_k), x_k пробегает всевозможные значения X.

p(x_k) – дискретная плотность распределения.

F(X)=p(X<x)= Σ _xk<X p(x_k)

Свойства дискретной плотности распределения.

1. p(x)>=0, p(x)<=1

2. Σ_k p(x_k)=1

Случайная величина Х имеет абсолютное непрерывное распределение, если существует такая функция p(x)>=0, т.ч. F(x)= ∫^x_-∞ p(t) dt

p(x) – плотность распределения случайной величины Х. p(x)=F'(x)

Свойства плотности распределения.

1. p(x)>=0

2. ∫^+∞_-∞ p(x) dx =1

16.

Математическое ожидание.

EX – мат.ожидание

EX=Σ^∞_i=1 x_i*p_i – для дискретных случайных величин

EX = ∫^+∞_-∞x*p(x) dx – непрерывная случайная величина

Механическая интерпретация мат.ожидания – центр масс системы.

Свойства мат. ожидания.

1. E(aX+bY)=aEX+bEY

2. EX>=0, если Х>=0 2a. X>=0 и EX=0 => X=0 с вероятностью 1.

3. Y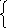=φ(X) => EY=Eφ(X)= Σ^∞_i=1 φ (x_i)*p(X=x_i) – дискр. случ. величина.

∫^+∞_-∞ φ(x)*p(x) dx

4. Y= φ(X,Y)

EY= Σ_i,j φ (x_i, y_i)*p(X=x_i,Y=y_i) -дискр.случ.вел.

∫^+∞_-∞ ∫^+∞_-∞ φ(x,y)*p(x,y) dx dy

5. EC=C, C-const

6. Если случайные величины не зависимы X и Y и имеют математическое ожидание, то математическое ожидание произведения, есть произведение математических ожиданий.

E(XY)=EX*EY

Это распространяется на любое число сомножителей

18.

Дисперсия случайной величины.

DX = EX(X-EX)² – математическое ожидание квадрата отклонения случайной величины от его математического ожидания.

Дисперсия – степень компактности, насколько сконцентрировано значение случайной величины вокруг математического ожидания.

Свойства дисперсии.

1. D(X)>=0

2. D(X)=0  X=C=EX

3. D(X+C)=DX

4. D(CX)=C²D(X)

5. Если X и Y независимы, то D(X+Y) = DX+DY

Распространяется на любое число независимых слагаемых.

6. D(X)= EX² – (EX)²

19.

Мат. ожидание и дисперсия нормального закона

Нормальное распределение - p(x) = 1/(√(2π)* σ)*exp(-(x-m)²/(2σ²))

Математическое ожидание – EX= ∫^+∞_-∞ x p(x) dx=m

Дисперсия D(X)= σ²

20.

Мат. ожидание и дисперсия биноминального распределения

Биноминальное распределение - p(X=m)= C_n^m p^m q^n-m

Математическое ожидание EX=np

Дисперсия DX=npq

21.

Мат. ожидание и дисперсия закона Пуассона

Закон Пуассона p(X=k)=λ^k/k!*e^-λ, λ>0, k=0,1,2…

Математическое ожидание – EX= λ

Дисперсия DX= λ

22.

Ковариация.

Мера зависимости X,Y

cov (X,Y)=E((X-EX)(Y-EY))=E(XY)-E(X)*E(Y)

Коэффициент корреляции.

ρ= ρ(X,Y)=cov(X,Y)/( √(DX)* √(DY))

Свойства коэффициента корреляции

1. cov(X+C₁,Y+C₂)=cov (X,Y) ; ρ(X+C₁,Y+C₂)= ρ(X,Y)

2. cov (C₁X,C₂Y)=C₁C₂ cov(X,Y); ρ(C₁X,C₂Y)=C₁C₂/ |C₁C₂| * ρ(X,Y)

3. если X,Y независимы, то cov(X,Y)= ρ(X,Y)=0 ; обратное неверно

4. -1<=ρ<=1

если ρ=1  Y=aX+b и а>0

ρ=-1  Y=aX+b и а<0

Коэффициент корреляции – мера линейной зависимости между X и Y

Двумерное нормальное распределение.

(Плотность распределения двумерного нормального вектора).

Вектор (X,Y)

EX=m₁, EY=m₂, DX=σ₁², DY= σ₂²

ρ – коэффициент корреляции X,Y

p(X,Y)=1/(2π* σ₁ σ₂* √(1- ρ²))*exp {1/(2(1- ρ²))*[ (x-m₁)²/ σ₁² + (y-m₂)²/ σ₂² - 2ρ*(x-m₁)*(y-m₂)/( σ₁* σ₂) ] }

23.

Случайные векторы

^-X^- = (X₁,X₂…X_n) – случайный вектор – набор случайных величин

^-X^- = ^-X^- (ω)

{ω: ^-X^- (ω)<^-a^-}

^-a^- <^-b^-  (a₁<b₁…a_n<b_n)

АЄßⁿ

{ω: X(ω) Є A}

Распределение случайного вектора

АЄßⁿ

μ(A) = p(X(ω) ЄA)=p(B) B={ω: X(ω) Є A}

Совместная функция распределения случ. вектора

F(^-x^-)=P(^-X^- < ^-x^-)=P(X₁<x₁…X_n<x_n)=F(x₁,…,x_n)

Плотность распределения

p(^-x^-) – плотность распределения случайного вектора ^-X^-

Непрерывный случ. вектор - F(^-x^-)= ∫^-x-_-∞ p(^-t^-) d^-t^- = ∫^x1_-∞ dt₁ … ∫^xn_-∞ p(t₁…t_n) dt_n

Дискретный случайный вектор - - F(^-x^-)= Σ_-Xk-<-x- p(^-X^-= ^-x_k^-)= Σ_-Xk-<-x- p(^-x_k^-)

Свойства функции распределения случ. векторов.

1. 0<=F(x₁..x_n)<=1

2. F(x₁..x_n) – не убывает по каждой переменной

3. lim F(x₁…x_n)=1

x₁ ∞

…..

x_n ∞

4. F(x₁..x_n) непрерывна слева по каждому аргументу

Свойства плотностей распределения.

1. p(x₁..x_n)>=0

2. p(x₁..x_n)= ∂ⁿ/(∂ x₁.. ∂x_n) * F(x₁..x_n)

3. ∫^+∞_-∞ dx₁ ∫^+∞_-∞ dx₂… ∫^+∞_-∞ p(x₁..x_n)dx_n=1

26.

Неравенство Чебышева.

Вспомогательное неравенство

Y>=0 случайная величина δ>0

p(Y> δ)<=EY/ δ

Основное неравенство

X-случ. величина DX< ∞ ε>0

P(| X-EX| > ε)<+ DX/ ε²

Закон больших чисел

a_na

X_n=X_n(ω)

Для всех ε>0 X_n^p X

X_n сходится по вероятности к Х если для всех ε P(| X_n –X|> ε)0 при n0

Среднее арифметическое случайных величин стремится к постояннjq: (X₁+^…+X_n ) /n a при n ∞

Если EX_i=m и DX_i<C, то (X₁….X_n)/n ^p m (сходится по вероятности)

27.

Характеристическая функция

f_x(t)=Ee^itX=Ecos(tX)+iEsin(tX)

f(t)=Σ_k p_k e^itxk

f(t)= ∫^+∞_-∞ e^itx p(x) dx

Характеристическая функция определена для любых t и для всех случайных величин X.

f(t)= ∫^+∞_-∞ e^itx dF(x)

dF(x)=p(x)dx dF(x)=F(xt)-F(x)

Свойства характеристических функций

1. f(0)=1

2. | f(t) | <=1

3. Y=aX+b

f_y=e^itb*f_x(at)

4. Если X и Y независимы, то f_x+y(t)=f_x(t)*f_y(t)

5. Если E|X|ⁿ< ∞, тогда f_x(t) имеет n-ю производную и f⁽ⁿ⁾(t)=(i)ⁿ EXⁿ e^itX

6. f(t) – равномерно непрерывна

7. E|x|ⁿ< ∞ f(t)=1+Σⁿ_k=1 f^k(0)/k! *t^k +o(tⁿ) – функция Тейлора для характеристической функции

8. Распределение случайной величины Х однозначно определяется ее характеристической функцией.

9. "Непрерывность"

Существует Х, F(x), f(t)

………….

X_n , F_n(x), f(t)

Равносильны два факта

а) F_n(x)  F(x) в каждой точке непрерывной функции F(x)

b) f_n(t) f(t) для всех t

29.

Центральная предельная теорема Леви.

X₁….X_n – последовательность независимых случайных величин.

EX=m, DX=σ²

P((x₁+..+x_n-nm)/ (σ*√n)<x)_n∞Φ(x)

Φ(x)=1/(√(2π)) ∫^x_-∞ exp(-t²/2) dt

30.

Производящие функции.

X>=0 – случайная величина X ЄZ

P(X=k)=p_k для всех k

Производящей функцией называется функция: ψ(z)= Σ^∞_k=0 z^kp_k=Ez^x ; |z|<=1

Свойства производящих функций.

1. ψ(0)=p₀

2. ψ(1)=1

3. p_k-?

ψ(z)= Σ^∞_k=0 1/k! ψ^(k)(0) z^k

p_k=1/k! ψ^(k)(0) для всех k

Производящая функция однозначно определяет распределение

4. dⁿ/dzⁿ ψ(z)|_z=1 = Σ^∞_k=n k(k-1)…(k-n+1) z^k-1 p_k |_z=1=EX(X-1)…(X-n+1)

5. ψ_aX+b(z)= Σ^∞_k=0 z^ak+b p_k = z^b Σ^∞_k=0 z^akp_k=z^b ψ_x(z^a)

6. X,Y – независимые случайные величины

Ψ_x+y(z)= ψ_x(z)* ψ_y(z)

32.

Условное мат. ожидание

Усл. мат. ожидание случайной величины Y при X=x – E_x(Y) –функция от x

Свойства условного математического ожидания.

1. Если Z=g(X), где g – некоторая неслучайная функция от Х, то E_z(E_x(Y))=E_z(Y)

В частности E(E_x(Y))=E(Y) (правило повторного ожидания)

2. Если Z=g(X), то E_x(ZY)=ZE_x(Y)

3. Если случайные величины X и Y независимы, то E_x(Y)=E(Y)

33.

Условное распределение.

Вектор (X,Y)

p(x,y) – совместная распределение

p₁(x)= ∫^+∞_-∞ p(x,y) dx – распределение величины x

p₂(y)= ∫^+∞_-∞ p(x,y) dy – распределение величины y

Условное распределение p(x/Y)=p(x,y)/p₂(y)

E(X/Y)= ∫^+∞_-∞ x p(x/Y) dx Y-фиксировано

cov (X,Y) =E(X-EX)(Y-EY)=EXY-EXEY

ρ(X,Y)=cov(X,Y)/√(DX DY)

X=(x₁ x₂)^T

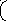
R₁ 0

R= 0 R₂

R₁- ковар. матрица x₁

R₂- ковар. матрица x₂

Для случайных векторов ^-x^- и ^-y^-

p(^-x^-/^-y^-)=p(^-x^-,^-y^-)/ p₂(^-y^-)=∫^+∞_-∞ p(^-x^-,^-y^-) d^-x^-

p(^-x^-/^-Y^-)

E(^-x^-/^-Y^-)=∫^+∞_-∞ ^-x^- p(^-x^-/^-Y^-) d ^-x^-

X₁ и X₂ – 2 подвектора вектора ^-X^-

R₁₁ R₁₂

R= R₂₁ R₂₂ - ковариационная матрица

R₁₁ – s*s

R₂₂ – m*m

X – n- мерный

X₁ – s – мерный

X₂ – m – мерный

s+m=n

E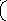X=m= m₁

m₂

E(X₁/X₂)=R₁₂ R₂₂^-1 (X₂-m₂) +m₁ и является нормальным случайным вектором N с мат. ожиданием m₁ и ковар. матрицей R₁₂R₂₂^-1R₂₁

34.

Марковские цепи.

Имеется некоторая система, которая может находится в некотором числе состояний а₁…а_n

Будем считать, что имеются моменты времени, в которые система переходит из одного состояния в другое. a_i0  a_i1  … a_ik

n=1 n=1 n=k

Заменим состояния числами 1…n

i₀  i₁  …  i_k за к моментов времени.

Переходы являются случайными. Возникает вероятности: p(i_k/ i_k-1…i₀) – в момент времени к

i_k-1…i₀ – предшествующие состояния.

x₀….x_n – случайные состояния системы.

x_i Є (0..n)

p(x_k=i_k/x_k-1=i_k-1…x₀=i₀)

Система обладает Марковским свойством, если p(x_k=i_k/x_k-1=i_k-1…x₀=i₀)= p(x_k=i_k/x_k-1=i_k-1) = (информация о предыдущих состояниях забыта) = p_k (i_k-1, i_k)=p(i_k-1, i_k) – если выполнено последнее равенство, то цепь Маркова однородна, т.е. не зависит от момента времени, а зависит только от состояния.

Для однородных цепей Маркова p_ij – вероятность перехода из состояния i в состояние j за один такт.

Матрица перехода за один шаг P. Элементы этой матрицы p_ij>0. Матрица вырожденная – сумма элементов каждой строки равна 1.

Распределение в момент времени k: q^(k)=(q₁^(k)…q_n^(k)), q_i^(k)=P(X_k=i).

Распределение Марковской цепи определено двумя объектами – q⁽⁰⁾ и P.

q⁽⁰⁾ =(q₁…q_n), q_i⁽⁰⁾=P(x₀=i) – начальное распределение

Формула Чепмена – Колмогорова (формула полной вероятности в ситуации, связанной с Марковскими цепями)

p_ij(n+m)=Σ^N_r=1 P_i,r(n)*P_r,j(m) для всех i,j или P^(n+m)=P⁽ⁿ⁾ P^(m) (равносильные формулировки)

35.

Классификация состояний Марковских цепей.

Два состояния i и j. j достижима из i (i j), если существует n т.ч. p_ij(n)>0

Два состояния сообщаются, если j достижима из i и i достижима из j. (ij)

Несущественное состояние – из него можно выйти, а нельзя попасть из других. (i)

Поглощающее состояние – можно попасть, но не выйдешь.

Если цепь находится в классе некоторых сообщающихся состояний, но она из него не выходит.

Периодичность.

Период состояния i – d_i – НОД для тех n, при которых p_ii(n)>0

Все периоды одинаковы для цепей с одним классом сообщающихся состояний, поэтому можно говорить о периоде всей Марковской цепи d.

36.

Классификация по возвратности.

Число состояний бесконечно. Состояние i возвратно, если вероятность когда-либо в него вернуться равна 1.

V_n-вероятность вернуться впервые на n шаге.

V_n=P_i(X₁≠I,…,X_n-1≠I, X_n=i)

Σ^∞_n=1 V_n=P_i =1 – вероятность возвращения.

Критерий возвратности

Теорема: Состояние i возвратно  когда Σ^∞_n=1 P_ii(n)= ∞

Следствия из критерия возвратности

1. Возвратность, это не свойство отдельного состояния, а свойство класса сообщающихся м/д собой состояний. Если i и j сообщаются и если одно возвратно, то и другое возвратно и наоборот.

2. Если цепь возвратна, то она возвратна в каждое свое состояние бесконечное число раз.

3. Если цепь состоит из одного класса сообщающихся состояний (конечное число), то цепь обязательно возвратна. Если цепь производит бесконечное число шагов через конечное число состояний, то ч/з одно она пройдет бесконечное число раз. По следствию 2 – цепь возвратна. Если цепь разбивается на к.-л. классы, то просто анализируется класс и не цепь, а класс будет возвратен.

Стационарное распределение Марковской цепи.

q⁽ⁿ⁾ = (q₁⁽ⁿ⁾ …q_N⁽ⁿ⁾)

q_i⁽ⁿ⁾ = P(X_n=i)

q⁽ⁿ⁾ не зависит от (n) – стационарная цепь.

q⁽ⁿ­­⁺¹⁾=q⁽ⁿ⁾ * P

Если существует стационарное распределение, то q=qP, Σ_i q_i = 1, q_i >=0

Стационарное распределение существует не всегда

q(P-E)=0

37.

Эргодическая теорема.

{1…N} существует n₀ т.ч. P_i,j⁽ⁿ⁰⁾>=0

Тогда существует набор π₁.. π_j >0 т.ч. Σ^N_j=1 π_j=1

P_ij⁽ⁿ⁾  π_j при т ∞

π = (π₁.. π_N) – вектор – стационарное распределение данной Марковской цепи

π= π*P

q_ij⁽ⁿ⁾  π_j для всех j при n ∞

Какое бы не было начальное распределение, цепь со временем приближается к стационарному распределению. (Цепь выходит на стационарное распределение).

38.

Закон больших чисел для цепей Маркова.

Схема Бернулли

m/n^p p при n ∞

x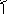_l= 1, успех

0, неудача

m/n= 1/n Σ^N_k=1 x_k – среднее число единиц

x₀ – состояние с номером i (фиксированное состояние)

x₀=i

j – фиксировано

þ_ij = 1/(n+1) Σⁿ_k=1 |_j(x_k) – среднее число посещений состояния j

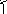|_j(x_k) = 1, x_k=j

0, x_k≠j

В условиях эргодической теоремы þ_ij ^p π_j

39.

Модель Эренфеста

Две урны с веществом. Между ними щель, в которую проходят частицы. Сначала в первой урне – i частиц, во второй m-i

Рассматривается Марковская цепь

Х_n – число частиц в первой урне

Найти матрицу переходных вероятностей

Вычислить стационарное распределение

Вычислить математическое ожидание числа частиц в первой урне

Матрица пишется в зависимости от числа частиц в первой урне.

k-й столбец: k-я строка - 0, (k-1) – я стр. – (m-k+1)/m, (k+1) – я стр. – (k+1)/m. Остальные нули.

Стационарное распределение находится из решения системы π (P-E)=0

π₀ = 1/2^m, π_k = C^k_m / 2^m k=0,…m

Мат. ожидание EX=Σⁿ_k=0 k C^k_m / 2^m = m/2 (половина всех частиц)