Шпора ТВИМС

(54)

   Доказательство:    Обозначим через величину , т.е. среднюю арифметическую n случайных величин. Случайная величина имеет математическое ожидание  

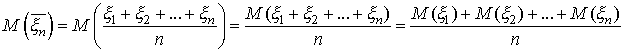
   и дисперсию  

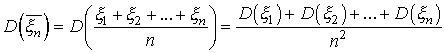
   (здесь мы воспользовались свойствами математического ожидания и дисперсии). Применяя к случайной величине вторую лемму Чебышева, найдем, что  

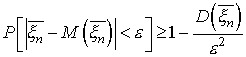
   т.е.  

   так как при любом i, и следовательно,  

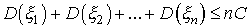
   Учитывая, что вероятность любого события не превосходит единицы, получим  

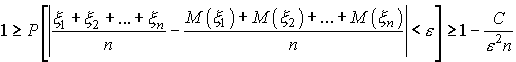
   Переходя к пределу при , имеем  

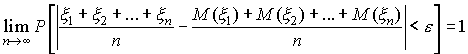
Теперь тетр.

Теорема Бернулли

            Пусть производится п независимых испытаний, в каждом из которых вероятность появления события А равно р.

            Возможно определить примерно относительную частоту появления события А.

 

            Теорема. Если в каждом из п независимых испытаний вероятность р появления события А постоянно, то сколь угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний р достаточно велико.

            Здесь т – число  появлений события А. Из всего сказанного выше не следует, что с увеличением число испытаний относительная частота неуклонно стремится к вероятности р, т.е. 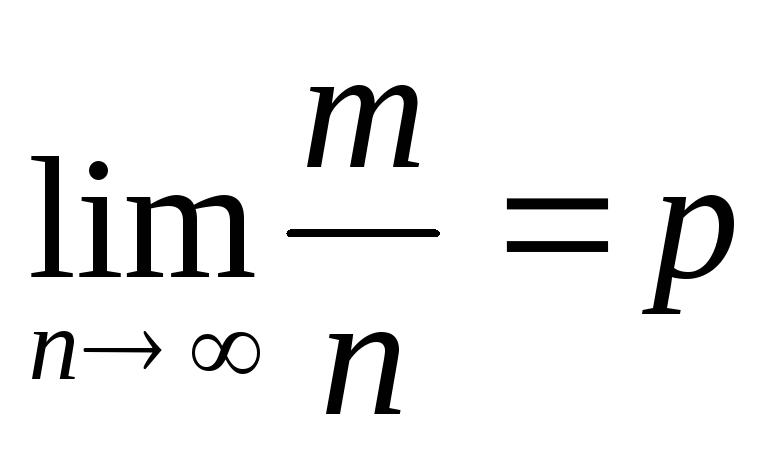. В теореме имеется в виду только вероятность  приближения относительной частоты к вероятности появления события А в каждом испытании.

32