1 Дифференциальное уравнение (ду) первого порядка, его решения (частные и общее).
Частный и общий интегралы дифференциального уравнения.
Иногда частное или общее решение уравнения удается найти только в неявной форме: f(x, y) = 0 или G(x, y, С1, С2, ..., Сn) = 0.
Такие неявно заданные решения называются частным интегралом или общим интегралом уравнения.
Интегральной
кривой
называется график
решения геометрически неопределённого
интеграла
(первообразной),
представляющего собой семейство
«параллельных» кривых
,
где каждому числу С соответствует
определенная кривая семейства. График
каждой кривой и называется интегральной
кривой.
Интегральные кривые для
.
З
адача
Коши и её геометрическая интерпретация
Геометрический смысл задачи Коши заключается в том, чтобы во множестве всех интегральных кривых системы найти ту, которая проходит через точку (t0, x0)
Постановка задачи Коши. Общий вид ОДУ без выделения вектора произвольных постоянных C таков F(t, J(m)x) = 0.
(а) Геом интерпретация задачи Коши для ДУ 1-го порядка [ y' = f ( x , y ), y(xo) = yo ]: Найти интегральную кривую дифф уравнения y' = f ( x , y ), проходящую через данную точку Mo(xo; yo).
|
Теорема существования и единственности решения задачи Коши.
Пусть
функция
непрерывна
в области
и
удовлетворяет в этой области одному из
трех условий:
А:
функция
удовлетворяет условию Липшица по
:
,
В:
существует и ограничена частная
производная
,
D: существует и непрерывна частная производная .
2 Геометрический смысл дифференциального уравнения
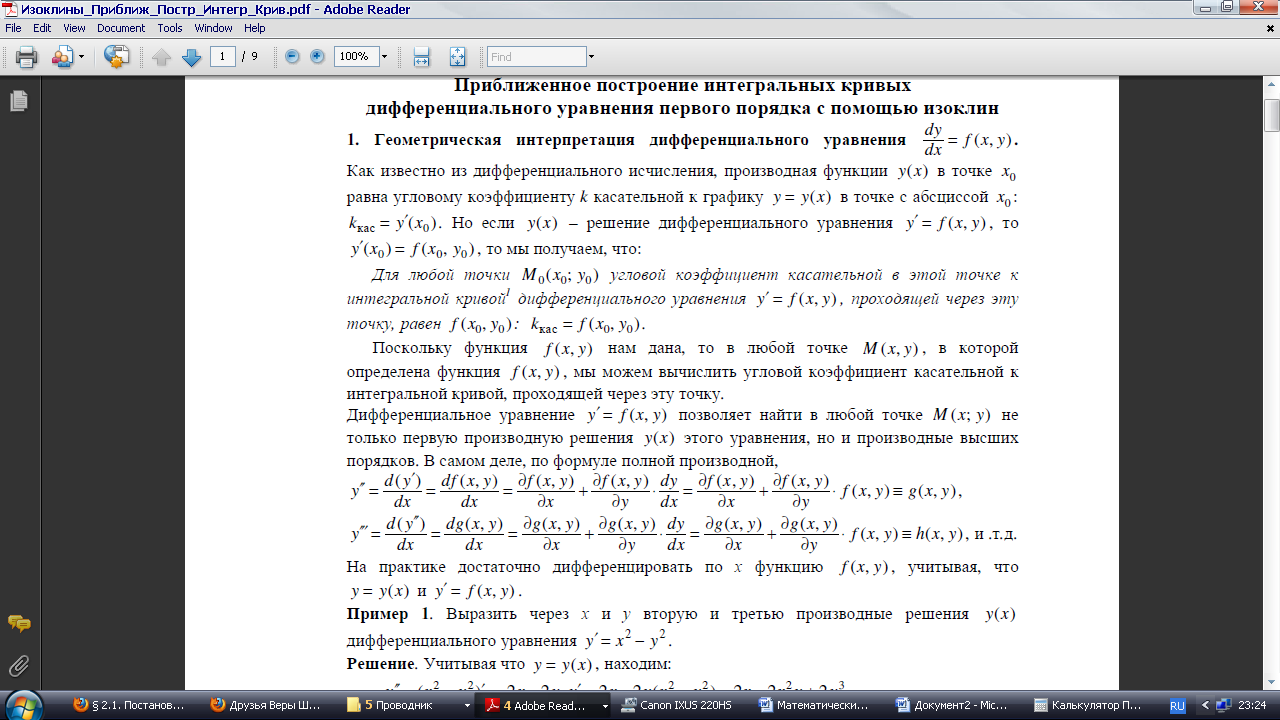
Изоклины и их применение для приближенного геометрического построения интегральных кривых для ДУ первого порядка.
3 Классы ДУ 1-го порядка
1) ДУ с разделяющими переменными
Уравнение с разделяющимися переменными имеет вид
.
В
этом уравнении переменные «можно
разделить», т.е. функции от x
и dx собрать в правую часть,
а функции от y и dy
– в левую часть. Затем интегрируем
полученное соотношение и получаем
соотношение вида
.
.
y' = f (x) g ( y)
y' =
.
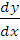Разделить переменные.
Проинтегрировать.
2) ДУ с однородной правой частью
Правая
часть однородного уравнения зависит
от отношения
:
.
Это
позволяет заменить отношение новой
переменной
или
.
.
Получено
уравнение с разделяющимися переменными.
Если
,
то исходное уравнение уже является
уравнением с разделяющимися переменными.
3) ДУ линейные
Существует два метода решения линейного уравнения: метод вариации произвольной постоянной и метод подстановки.
Метод вариации произвольной постоянной будет встречаться нам часто: при решении неоднородных линейных уравнений высшего порядка, при решении неоднородных систем линейных уравнений.
При решении методом вариации произвольной постоянной сначала решают однородное уравнение (с нулевой правой частью)
Это – уравнение с разделяющимися переменными.
.
Затем
варьируют произвольную постоянную,
полагая
.
.
Подставляем в неоднородное уравнение:
.
При вариации произвольной постоянной здесь обязательно должны сократиться два члена, в этом идея метода.
,
где С – произвольная постоянная.
.
Видно, что общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения. Это справедливо не только для линейных уравнений первого порядка, но и для линейных уравнений высших порядков, и для линейных систем. Там подобное утверждение называется теоремой о структуре общего решения неоднородного уравнения или системы.
Замечание.
Решая уравнение методом вариации,
обязательно приводите его к виду
(если при
стоит
коэффициент, то делить на него обязательно),
иначе метод вариации даст ошибку.
При решении методом подстановки полагают
.
Мы видели выше, что решение действительно
является произведением двух функций
от x. Этот факт здесь и
используется.
.
Подставляем в уравнение:
.
Теперь
решают либо уравнение
,
определяя отсюда
,
либо уравнение
,
определяя отсюда
.
Здесь при интегрировании не надо
добавлять константу, она появится позже,
при отыскании второй функции. В первом
случае, остается найти v
из
.
Теперь
=
,
как и выше.
Во
втором случае остается найти u
из
,
.
Теперь = , как и выше.