1. Способы задания нечеткой импликации. Привести примеры.

Нечеткой импликацией или просто — импликацией нечетких высказываний и (записывается как: и читается — "из следует ", "ЕСЛИ , ТО ") называется бинарная логическая операция, результат которой является нечетким высказыванием, истинность которого может принимать значение, определяемое по одной из следующих формул.

1). Классическая нечеткая импликация, предложенная Л. Заде:

Т( ) = max{min{T( ), Т( )}, 1– T( )}. (1)

Эту форму нечеткой импликации называют также нечеткой импликацией Заде.

2). Классическая нечеткая импликация для случая T( ) T( ):

Т( ) = max{T(¬ ), Т( )}= max{1–T( ), Т( )}. (2)

Эту форму нечеткой импликации иногда называют нечеткой импликацией Гѐделя.

3). Нечеткая импликация, предложенная Э. Мамдани:

Т( ) = min{T( ), Т( )} (3)

Эту форму нечеткой импликации также называют нечеткой импликацией Мамдани

или нечеткой импликацией минимума корреляции.

4). Нечеткая импликация, предложенная Я. Лукасевичем:

Т( ) = min{1, 1–T( )+Т( )} (4)

Эту форму нечеткой импликации также называют нечеткой импликацией Лукасевича.

5). Нечеткая импликация, предложенная Дж. Гогеном:

Т( ) = min{1, T( )/Т( )} где Т( )>0 (5)

Эту форму нечеткой импликации также называют нечеткой импликацией Гогена.

6). Нечеткая импликация по формуле граничной суммы:

Т( ) = min{1, T( )+Т( )} (6)

7). Нечеткая импликация по формуле произведения:

Т( ) = T( )+Т( ). (7)

8). Нечеткая импликация, предложенная Н. Вади:

Т( ) = max{T( )∙Т( ), 1– T( )}. (8)

Нечеткая импликация играет важную роль в процессе нечетких логических рас-

суждений. Так же, как и в математической логике первый ее операнд (нечеткое высказывание) называется посылкой или антецедентом, а второй — заключением или консетентом.

Хотя классическая нечеткая импликация находит наибольшее применение при решении

прикладных задач и она остается справедливой в случае обычных высказываний классической логики, остальные способы вычисления нечеткой импликации в отдельных ситуациях оказываются более эффективными с вычислительной точки зрения.

Пример 7.4. Рассмотрим составное нечеткое высказывание в форме нечеткой имплика-

ции: "Если О. Бендер имеет довольно высокий рост, то завтра будет пасмурная погода",

при этом представим, что истинность входящих в него элементарных нечетких высказываний равна T( ) = 0.7 и T( ) = 0.2. Тогда истинность этой нечеткой импликации, вычисленная по основной формуле (1), равна Т( ) = 0.3, по формуле (3) — Т( ) = 0.2, по формуле (4) — Т( ) = 0.5, по формуле (5) — Т( ) = 0.29, по формуле (6) —Т( ) = 0.9, по формуле (7) — Т( ) = 0.14, по формуле (8) — Т( ) = 0.3

2. Выбор оптимальных проектов в нечеткой среде.

Метод решения задачи принятия слабоструктурированных решений (ПССР) в условиях нечеткой неопределенности изображен на рисунке.

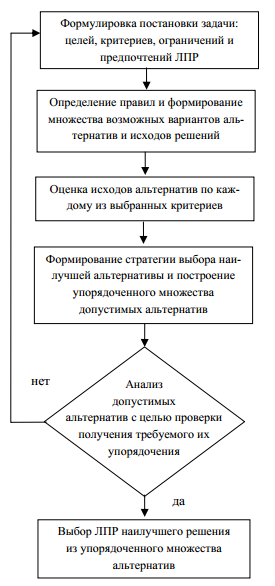
рисунок

На первом этапе формулируется постановка задачи: цели, критерии, ограничения и предпочтения ЛПР. На втором этапе определяются правила, на основе которых формируется множество возможных для рассматриваемой ситуации вариантов альтернатив решений и соответствующих им исходов. На третьем этапе осуществляется оценка исходов альтернатив по каждому

из выбранных критериев. На четвертом этапе строится (или выбирается) решающее правило – стратегия определения и выбора наилучшей альтернативы в соответствии с критериями и предпочтениями ЛПР. На основе этой стратегии формируется упорядоченное множество допустимых альтернатив – предпочтительных из возможных

для текущей ситуации. Анализ допустимых альтернатив определяет, получено ли требуемое упорядочение альтернатив. Если не получено, то возвращаются к предыдущим этапам для осуществления соответствующих уточнений и корректировок параметров построенных моделей и правил исходной задачи. Если требуемое упорядочение получено, то из него ЛПР выбирает наилучшее решение с учетом личных предпочтений.

Во многих задачах ПР в нечеткой среде результат выбора той или иной альтернативы в качестве решения оценивается нечетким числом. Для m альтернатив формируется m базовых нечетких чисел-оценок. При наличии n возможных исходов каждой альтернативы образуется mn нечетких чисел-оценок. При этом количество их значений равно количеству базовых чисел-оценок (m). Для решения таких задач предлагаются модифицированные − нечеткие аналоги известных критериев, например байесовского и дисперсии.