
- •Глава 2
- •§1 Основные математические понятия.
- •§2 Макроскопические и микроскопические системы. Постулат равновероятности. Эргодическая гипотеза. Статистический вес. Флуктуации.
- •§3 Распределение Больцмана.
- •§4 Распределение Максвелла.
- •§5 Основное уравнение молекулярно-кинетической теории идеальных газов.
- •§6 Функция Больцмана
- •§7 Распределение энергии по степеням свободы.
- •§8 Статистики Ферми-Дирака и Бозе-Эйнштейна.
- •Глава 3. Процессы переноса.
- •§1 Длина свободного пробега, среднее число столкновений.
- •§2 Явления переноса.
- •§3 Молекулярная теория явлений переноса в газах.
- •Глава 4. Реальные жидкости и газы.
- •§1 Силы и потенциальная энергия межмолекулярного взаимодействия.
- •§2. Уравнение Ван-дер-Ваальса
- •§ 3. Изотермы Ван-дер-Ваальса и их анализ.
- •Часть 7—6 — отвечает газообразному состоянию;
- •Часть 2—1 — жидкому;
- •Часть 6—2, — горизонтальный участок, соответствующий равновесию жидкой и газообразной фаз вещества.
- •§ 4. Внутренняя энергия реального газа
- •§ 5. Свойства жидкостей. Поверхностное натяжение
- •§ 6. Смачивание
- •§ 7. Давление под искривленной поверхностью жидкости
- •§ 8. Капиллярные явления
- •§ 9. Испарение, сублимация, плавление и кристаллизация. Аморфные тела
- •§10. Фазовые переходы I и II рода
- •§ 11. Диаграмма состояния. Тройная точка
Глава 2
§1 Основные математические понятия.
Как мы раньше говорили, с одной стороны, информация о положениях и скоростях всех отдельных частиц системы идеального газа является наиболее полной мыслимой информацией, а с другой стороны, в своей непосредственной форме она неприменима для анализа свойств и поведения системы. Чтобы информацию, содержащуюся в этих сведениях, можно было использовать, необходимо свести ее к некоторым обобщенным характеристикам совокупности частиц таким образом, чтобы они отражали наиболее существенные свойства этой совокупности, были бы легко обозримыми и сформулированными математически. Эти вопросы разработаны в теории вероятностей и математической статистике.
Разделим
объем, который занят идеальным газом,
на две равные части. Будем считать, что
можем различать частицы и следить за
положением отдельной частицы, не оказывая
актом наблюдения существенного влияния
на ее движение и состояние наблюдаемой
системы в целом. Допустим, что система
находится в неизменных внешних условиях.
Рассмотрим событие, состоящее в том,
что изучаемая частица находится в одной
из половин объема. Тогда результат
каждого наблюдения сводится к утверждению,
что событие либо произошло, т.е. частица
находится в данной половине объема,
либо не произошло, т.е. ее нет в этой
половине. Обозначим
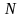 - общее число наблюдений или «испытаний»;
- общее число наблюдений или «испытаний»;
 - число испытаний, когда событие произошло,
т.е. частица находилась в рассматриваемой
половине объема;
- число испытаний, когда событие произошло,
т.е. частица находилась в рассматриваемой
половине объема;
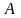 - само событие. Вероятность
наступления события
определяется формулой:
- само событие. Вероятность
наступления события
определяется формулой:

Здесь
существенно очень большое
 число испытаний в системе, находящейся
в неизменных условиях. Вместо требований
испытаний над одной и той же системой
в неизменных условиях можно говорить
о совокупности отдельных испытаний над
большим числом одинаковых систем. Это
большое число одинаковых систем
называется ансамблем
систем.
число испытаний в системе, находящейся
в неизменных условиях. Вместо требований
испытаний над одной и той же системой
в неизменных условиях можно говорить
о совокупности отдельных испытаний над
большим числом одинаковых систем. Это
большое число одинаковых систем
называется ансамблем
систем.
Для непрерывных случайных величин вводится понятие плотности вероятности. Плотностью вероятности равняется вероятность нахождения молекулы в бесконечно малом объеме, отнесенном к этому объему:
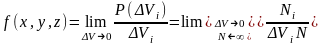 ,
где
,
где
 - координаты точки, к которой стягивается
бесконечно малый объем
- координаты точки, к которой стягивается
бесконечно малый объем
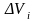 .
.
Случайная величина считается заданной, если заданы спектр ее значений и функция распределения плотности вероятности принимать эти значения. Функция плотности вероятности является непрерывной, дифференцируемой, конечной и нормированной на 1.
Из
этого определения следует, что если
произвести
 наблюдений, то в объеме
наблюдений, то в объеме
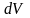 в окрестности точки
в окрестности точки
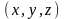 молекула будет обнаружена в
молекула будет обнаружена в
 случаях.
случаях.
В
конечном объеме
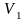 молекула окажется обнаруженной
молекула окажется обнаруженной
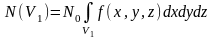 раз. Отсюда следует, что вероятность
раз. Отсюда следует, что вероятность
 быть обнаруженной при наблюдении в
объеме
для молекулы равна:
быть обнаруженной при наблюдении в
объеме
для молекулы равна:
 .
.
Если
в качестве объема взять все пространство
 ,
то при каждом испытании частица окажется
в какой-то точке пространства и,
следовательно, число наблюдений частицы
в объеме
равно числу испытаний
,
т.е.
,
то при каждом испытании частица окажется
в какой-то точке пространства и,
следовательно, число наблюдений частицы
в объеме
равно числу испытаний
,
т.е.
 и следовательно вероятность нахождения
частицы в объеме равна единице. Условие
и следовательно вероятность нахождения
частицы в объеме равна единице. Условие
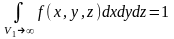
называется условием нормировки плотности вероятности. Оно выражает факт существования молекулы.
Среднее значение непрерывно изменяющейся величины (еще называют математическим ожиданием случайной величины с учетом вероятности):
 ,
,
где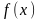 - плотность вероятности распределения
случайной величины х.
- плотность вероятности распределения
случайной величины х.
Дисперсия. «Разброс» величины около ее среднего значения характеризуется дисперсией. Она определяется средним квадратом отклонения рассматриваемой величины от ее среднего значения и задается формулой для непрерывной случайной величины:
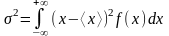
Корень квадратный из дисперсии называется стандартным или среднеквадратичным отклонением.
Функция
распределения вероятностей.
Вероятность того, что случайная величина
х
принимает значения, меньшие некоторого
заданного числа х0,
т.е.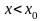 определяется формулой:
определяется формулой:
 .
.
Функция
 называется функцией
распределения вероятностей.
называется функцией
распределения вероятностей.
В
физике принято характеризовать
распределение вероятностей посредством
плотности вероятности. При этом слова
«плотность» и «вероятность» опускаются,
и говорится просто о распределении.
Например, функция
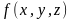 называется просто функцией распределения
координат. Можно говорить о функциях
распределения скоростей, импульсов и
т.д. вид функции распределения зависит
от физических условий, свойств частиц
и т.д. Однако имеются наиболее типичные
распределения, которые реализуются при
весьма общих физических условиях. Это
распределение Гаусса, Биномиальное
распределение, распределение Пуассона
и т.д.
называется просто функцией распределения
координат. Можно говорить о функциях
распределения скоростей, импульсов и
т.д. вид функции распределения зависит
от физических условий, свойств частиц
и т.д. Однако имеются наиболее типичные
распределения, которые реализуются при
весьма общих физических условиях. Это
распределение Гаусса, Биномиальное
распределение, распределение Пуассона
и т.д.
