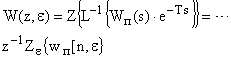11.3. Типовая структура импульсной системы.

 

Рис. 7. Расчетная схема импульсной САУ

 

• Если время замкнутого состояния ключа мало, то сигнал на его выходе можно заменить последовательностью 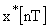дельта-функций, с площадью :

.

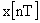• В таком случае реакция непрерывной части — это суперпозиция весовых функций 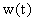, которую можно рассматривать и как непрерывный сигнал 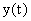, и как дискретную последовательность .

• Импульсным фильтром считают импульсный элемент (ключ) с непрерывной частью на выходе. За истинный сигнал фильтра принимают выходную последовательность только в дискретные моменты времени , где n = ..., -2, -1, 0, 1, 2,...

• Задача идеального импульсного элемента (ИИЭ) в модели — сформировать для дальнейшего математического описания системы либо последовательность импульсов типа -функций с площадью 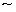, либо решетчатую функцию, в основе которой единичная импульсная функция 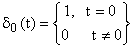с амплитудой .

• Задача экстраполятора — математически описать выходную последовательность реального импульсного звена (экстраполяция — это прогнозирование (синтез) сигнала между значениями решетчатой функции).

• Коэффициент передачи квантователя (ИИЭ) обратно пропорционален периоду квантования, а коэффициент передачи экстраполятора нулевого порядка равен периоду. Таким образом общий коэффициент передачи квантующей и восстанавливающей цепи, т.е. ИЭ обычно равен единице.

 

11.3.1.Обобщенная модель импульсного элемента

 

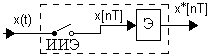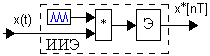
Рис. 8. Обобщенная модель импульсного элемента

 

Приведенные весовая и передаточная функции разомкнутой импульсной системы.

Если ИИЭ выдает решетчатую функцию, то можно ввести понятие "приведенной весовой функции" — . Это отношение выходного сигнала к значению единственной дискреты поданной на вход экстраполятора.

Если ИИЭ выдает последовательность типа функций, то для непрерывной части совместно с экстраполятором можно вывести понятие приведенной непрерывной передаточной функции:

,

при этом

.

 

Дискретная передаточная функция САУ

 

Знание приведенной решетчатой весовой функции позволяет найти реакцию импульсного фильтра на входную величину произвольного вида — . Рассмотрим реакции на отдельные значения входной величины в дискретные моменты времени:

• на

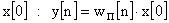
• на

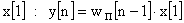
• на

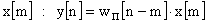
Следовательно реакция на всю входную последовательность будет равна:

;

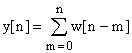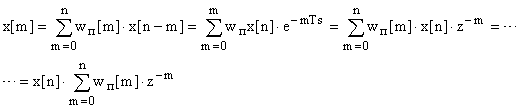
Здесь первоначально изменен порядок суммирования (свертка), а затем учли запаздывание оператором запаздывания . Если устремить n к бесконечности, то, очевидно, что сомножитель для есть дискретная передаточная функция:

.

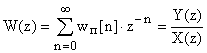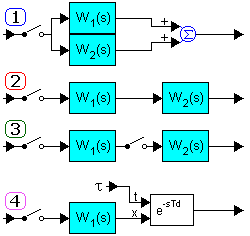
И поскольку она является Z-преобразованием приведенной решетчатой весовой функции, то ее можно представить как Z-преобразование от обратного преобразования Лапласа приведенной передаточной функции экстраполятора и непрерывной части:

.

Часто для краткости записи знак операции опускают записывая:

.

 

Правила преобразования структурных схем дискретных систем

 

те. !!! где: — относительное смещение, которое отсчитывается от начала предыдущего такта ( ; .

 

Передаточная функция системы с экстраполятором нулевого порядка и звеном запаздывания

 

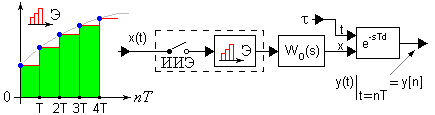
Рис. 9. Схема экстраполятора нулевого порядка

 

Экстраполятором нулевого порядка являются, во-первых – устройства “выборки-хранения” (УВХ) и, во-вторых, цифро-аналоговые преобразователи (ЦАП).

Найдем изображение Лапласа для единичного импульса:

.

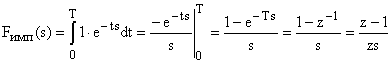Тогда Z-изображение экстраполятора и непрерывной части со звеном запаздывания:

,

где: ; ; не учитывает коэффициент передачи ИИЭ равный .

 

Передаточная функция системы с экстраполятором, осуществляющим АМ первого или второго рода

 

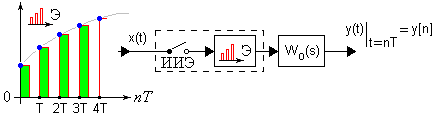
Рис. 10. Структурная схема импульсной САУ с экстраполятором нулевого порядка.

 

Найдем изображение Лапласа для частично заполненного импульса:

.

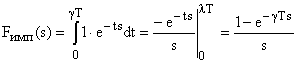Тогда Z-изображение экстраполятора и непрерывной части со звеном запаздывания:

,

где: ; не учитывает коэффициент передачи ИИЭ равный .

Если , то , тогда:

К этой формуле, в первом приближении, сводится и амплитудной модуляции второго рода.

 

Передаточная функция замкнутой импульсной системы

 

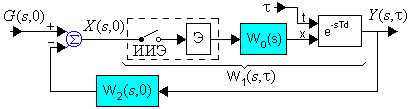
Рис. 11. Структурная схема импульсной САУ

 

Опишем систему в изображениях Лапласа:

.

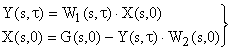Следовательно

.

Отсюда следует, что

или

те.:

.

Передаточная функция по ошибке может быть получена решением системы относительно ошибки .

Поскольку запаздывание не определяет свойства системы в области низких частот, практически всегда для оценки качества могут быть использованы формулы

Для учета особенности определения импульсной передаточной функции от последовательно включенных непрерывных блоков используется правило 2 преобразования структурных схем.

 

Передаточная функция для возмущений

 

Рис. 12. Структурная схема САУ с учетом внешних возмущений

 

Поскольку для произведения двух операторных многочленов: (изображение возмущения) и нельзя найти Z-преобразование раздельно, см. правило 2, то передаточную функцию по возмущению удобно определять для эквивалентных возмущений , приведенных к входу ИЭ:

.

 

Частотные передаточные функции импульсных систем

 

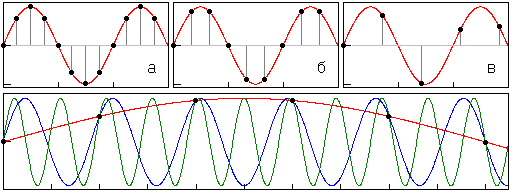
Рис. 13. Дискретная синусоидальная последовательность .

 

Особые свойства последовательности :

1. Функция может быть как периодической — рис. 13а и 13б, так и непериодической — рис. 13в.

2. Амплитуда образующей непрерывной функции может быть максимальным значением последовательности a — рис.13а, а может не является им — рис.13б.

3. Последовательность не изменится, если на вход ключа подавать сигналы с частотами, отличающимися на частоту дискретизации: .

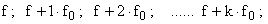Запишем закон изменения синусоидальной последовательности в экспоненциальной форме:

,

тогда выходная величина импульсного фильтра:

;

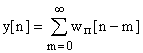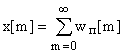
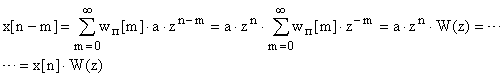
Таким образом, передаточная функция при подстановке — есть частотная передаточная функция САУ. Все остается в силе и для и .

Очевидно, что частотные передаточные функции , и обладают периодическими свойствами ( ). Это видно и из нижней части рис.13, поскольку одну и ту же входную последовательность могут вызывать входные сигналы с разными частотами .