
- •Введение
- •Пояснительная записка
- •Предмет изучения дисциплины
- •Цель и задачи дисциплины
- •Требования к уровню подготовки студента, завершившего освоение дисциплины (результат обучения)
- •Общая характеристика дисциплины и распределение учебного времени по видам занятий
- •Содержание программы
- •Тема 5. Транспортная задача
- •Раздел 3. Модели планирования и управления в сетях
- •Тема 6. Нелинейное программирование
- •Тема 7. Теория оптимального управления
- •Тема 8. Методы и модели сетевого планирования и управления
- •Раздел 4. Многокритериальные задачи и введение в теорию безкоалиционных игр
- •Тема 9. Методы решения многокритериальных операционных задач
- •Тема 10. Игровые модели операций
- •Раздел 5. Детерминированные и стохастические модели
- •Тема 11. Имитационное моделирование
- •Тема 12. Модели систем массового обслуживания
- •Тема 13. Модели управления запасами
- •Содержание самостоятельной работы студентов по дисциплине
- •Содержание индивидуальной работы студентов по дисциплине*)
- •Порядок текущего, модульного и итогового контроля академической успешности студентов, критерии оценки знаний
- •9.1. Шкала оценивания академической успешности студента по ects
- •9.2. Рейтинговая оценка академической успешности студента за семестр
- •Общие требования к оформлению самостоятельной работы.
- •Вариант № 13
- •Вариант № 19
- •Вариант № 25
- •Часть II.
- •Варианты 1-10
- •Варианты 11-20
- •Варианты 21-30
- •Варианты 1-10
- •Варианты 11-20
- •Варианты 21-30
- •Варианты 1-10
- •Варианты 11-20
- •Варианты 21-30
- •Варианты 1-10
- •Варианты 11-20
- •Варианты 21-30
- •Часть ш. Примеры решения задач Задание № 3. Задача об оптимальной производственной программе
- •Решение
- •Задание № 4. Задача сетевого планирования и управления
- •Решение
- •Задание № 5. Задачи систем массового обслуживания
- •6.1. Одноканальная система обслуживания
- •Решение
- •Многоканальная система в магазин, в среднем, в час заходят 30 человек. В магазине один продавец. Каждый покупатель находится в магазине около 12 мин..
- •Если принять на работу еще одного продавца, то на сколько изменятся следующие характеристики:
- •Решение
- •Задание № 7. Задачи управления запасами
- •7.1.Задача планирования дефицита
- •Решение При регулярных поставках товара можно использовать модель оптимального размера заказа с фиксированным временем его выполнения.
- •Тогда оптимальный размер заказа составит величину
- •Максимальный размер запаса за один цикл
- •7.2.Задача закупок со скидками
- •Решение
- •Тогда оптимальный размер заказа составит величину
- •Тогда оптимальный размер заказа составит величину
- •Тогда оптимальный размер заказа составит величину
- •Вопросы к экзамену по дисциплине «Методы оптимизации и исследование операций»
- •Литература
Часть ш. Примеры решения задач Задание № 3. Задача об оптимальной производственной программе
Предприятие планирует выпускать четыре вида продукции. Объемы ресурсов трех видов (в условных единицах - УЕ), затраты каждого ресурса на изготовление единицы продукции и цена единицы продукции (в условных денежных единицах - УДЕ) приведены в таблице.
Вид продукции Вид ресурса |
П1 |
П2 |
П3 |
П4 |
Объем (УЕ) |
Р1 |
3 |
2 |
4 |
5 |
4800 |
Р2 |
3 |
0 |
4 |
4 |
4200 |
Р3 |
10 |
8 |
6 |
8 |
10000 |
Цена на единицу продукции (УДЕ) |
48 |
50 |
45 |
50 |
|
Найти оптимальную производственную программу для получения наибольшей прибыли, считая сбыт любого количества продукции обеспеченным.
Вопросы:
Сколько продукции каждого вида следует производить?
Какова ожидаемая максимальная выручка от продажи продукции?
Выяснить, какой из ресурсов наиболее дефицитен, какой из видов продукции наиболее убыточен?
Определить пределы устойчивости двойственных оценок к изменению запасов ресурсов?
На сколько изменится максимальная выручка, если запасы ресурсов каждого вида уменьшатся на 100 единиц?
Решение
Для того, чтобы ответить на поставленные вопросы, необходимо:
а) построить модель исходной и двойственной задач;
б) решить исходную задачу симплексным методом;
в) найти оптимальное решение двойственной задачи;
г) дать экономическую интерпретацию основным и дополнительным переменным оптимальных решений исходной и двойственной задач.
Составим экономико-математическую модель данной (исходной) задачи (задачи об оптимальной производственной программе или задачи об оптимальном распределении ресурсов):
Z = 48x1 + 50x2 + 45x3 + 50x4 max, (1)
 3x1
+ 2x2
+ 4x3
+ 5x4
4800, (2)
3x1
+ 2x2
+ 4x3
+ 5x4
4800, (2)
3x1 + 4x3 + 4x4 4200, (3)
10x1 + 8x2 + 6x3 + 8x4 10000, (4)
xj
0,
![]()
а) Исходная задача записана в стандартной симметричной форме, поэтому построим двойственную ей ЗЛП, пользуясь правилами построения двойственных задач:
f = 4800у1 + 4200у2 + 10000у3 min (5)
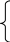 3у1 + 3у2
+10у3
48, (6)
3у1 + 3у2
+10у3
48, (6)
2у1 + 8у3 50, (7)
4у1 + 4у2 + 6у3 45, (8)
5у1 + 4у2 + 8у3 50, (9)
у1 0, у2 0, у3 0. (10)
б) Для решения ЗЛП симплексным методом необходимо ее записать в канонической форме
max Z = 48x1 + 50x2 + 45x3 + 50x4 + 0·(x5 + x6 + x7) (11)
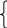 3x1
+ 2x2
+ 4x3
+ 5x4
+ x5
= 4800, (12)
3x1
+ 2x2
+ 4x3
+ 5x4
+ x5
= 4800, (12)
2x1 + 4x3 + 4x4 + x6 = 4200, (13)
10x1 + 8x2 + 6x3 + 8x4 + x7 = 10000. (14)
Решение задачи проводим в симплекс-таблицах (таблица 1.1). Первоначальный опорный план – допустимое базисное решение, которое получаем из расширенной матрицы А системы уравнений (12 – (14).

 3 2 4 5 1 0 0 4800
3 2 4 5 1 0 0 4800
А ~ 2 0 4 4 0 1 0 4200
10 8 6 8 0 0 1 10000
Таблица 1.1
Номер |
Базисные переменные |
Ci б |
План bi |
48 |
50 |
45 |
50 |
0 |
0 |
0 |
Qij=bi /aij |
|
симплекс-таблицы |
строки i |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
|
|||
I |
1 |
X5 |
0 |
4800 |
3 |
2 |
4 |
5 |
1 |
0 |
0 |
2400; 960 |
2 |
X6 |
0 |
4200 |
3 |
0 |
4 |
4 |
0 |
1 |
0 |
1050 |
|
3 |
X7 |
0 |
10000 |
10 |
8 |
6 |
8 |
0 |
0 |
1 |
1250; 1250 |
|
4 |
Zm = 0 |
Δ1=-48 |
Δ2=-50 |
Δ3=-45 |
Δ4=-50 |
Δ5=0 |
Δ6=0 |
Δ7=0 |
Q14=min; a14=5 - разреша-ющий элемент |
|||
II |
1 |
X4 |
50 |
960 |
3/5 |
2/5 |
4/5 |
1 |
1/5 |
0 |
0 |
2400 |
2 |
X6 |
0 |
360 |
3/5 |
-8/5 |
4/5 |
0 |
-4/5 |
1 |
0 |
|
|
3 |
X7 |
0 |
2320 |
26/5 |
24/5 |
-2/5 |
0 |
-8/5 |
0 |
1 |
483,3 |
|
4 |
Zm = 48000 |
Δ1=-18 |
Δ2=-30 |
Δ3= -5 |
Δ4= 0 |
Δ5=10 |
Δ6=0 |
Δ7=0 |
Q32=min; a32=24/5-разреша-ющий элемент |
|||
Ш |
1 |
X4 |
50 |
2300/3 |
1/6 |
0 |
5/6 |
1 |
1/3 |
0 |
-1/12 |
920 |
2 |
X6 |
0 |
3400/3 |
7/3 |
0 |
2/3 |
0 |
-4/3 |
1 |
1/3 |
1700 |
|
3 |
X2 |
50 |
1450/3 |
13/12 |
1 |
-1/12 |
0 |
-1/3 |
0 |
5/24 |
|
|
4 |
Zm = 62500 |
Δ1=14,5 |
Δ2=0 |
Δ3=-7,5 |
Δ4=0 |
Δ5=0 |
Δ6=0 |
Δ7=6,25 |
Q13 = min; a13=5/6 –разреша-ющий элемент |
|||
IV |
1 |
X3 |
45 |
920 |
1/5 |
0 |
1 |
6/5 |
2/5 |
0 |
-1/10 |
|
2 |
X6 |
0 |
520 |
11/5 |
0 |
0 |
-4/5 |
-8/5 |
1 |
2/5 |
|
|
3 |
X2 |
50 |
560 |
11/10 |
1 |
0 |
1/10 |
-3/10 |
0 |
1/5 |
|
|
4 |
Zm = 69400 |
Δ1=16 |
Δ2 = 0 |
Δ3=0 |
Δ4= 9 |
Δ5= 3 |
Δ6=0 |
Δ7=5,5 |
Все Δj 0, отсюда план -оптимален |
|||
|
|
|
У4* |
У5* |
У6* |
У7* |
У1* |
У2* |
У3* |
|
||
По критерию оптимальности полученный план оптимален, т.е. х2*= 560, х3*= 920, х6*=520, х1*= х4*= х5*= х7*= 0, т.е. Х* = (0; 560; 920; 0; 0; 520; 0).
в) Из последней строки IV-ой симплекс-таблицы определяем оптимальный план двойственной задачи
Y* = (3; 0; 5,5; 16; 0; 0; 9).
Экстремальное значение целевой функции Zmax = fmin = 69400.
г) Оптимальное решение двойственной задачи (объективно-обусловленные оценки) Y* показывает, что производство продукции вида П2 и П3 (им соответствуют нулевые оценки y5 и y6) – рентабельно, а П1 и П4 – убыточно. Наиболее убыточным является производство П1 (т.к. 16>9). Дефицитный ресурс имеет положительную оценку, т.е. Р1 и Р3 – дефицитные ресурсы (запасы – х5 и х7 -равны нулю). Поскольку 5,5 > 3, то ресурс Р3 более дефицитен, чем Р1.
Для того, чтобы найти пределы устойчивости двойственных оценок к изменению запасов ресурсов, построим матрицу D, обратную к матрице Ã. В основной матрице коэффициентов А выберем векторы, соответствующие базисным переменным в оптимальном решении (х2, х3, х6).
 2 4 0
2 4 0
à ~ 0 4 1
8 6 0
Определитель матрицы
 2 4 0
2 4 0
Δ(Ã) = 0 4 1 = 20 ≠ 0,
8 6 0
т.е. обратная к Ã матрица существует. Транспонируем матрицу Ã
 2 0 8
2 0 8
ÃТ ~ 4 4 6
0 1 0
и к каждому элементу матрицы ÃТ найдем алгебраическое дополнение:
![]()
![]()
![]()
Аналогично, А21 = 8; А22 = 0; А23 = -2; А31 = -32; А32 = 20; А33 = 8.
Таким образом, матрица

 -6 0 4
- 0,3 0 0,2
-6 0 4
- 0,3 0 0,2
D = Ã-1 ~ (1/20) 8 0 -2 = 0,4 0 -0,1
-32 20 8 -1,6 1 0,4
По формулам (7) и (8) первого раздела данного пособия определим нижнюю и верхнюю границу интервалов устойчивости для каждого вида ресурса.
Сначала последовательно перенумеруем базисные перменные хk (k=1,2,3):
х1 =х2*= 560, х2 =х3*= 920, х3 = х6*=520.
Каждая строка матрицы D соответствует своей переменной хk (k=1,2,3), а каждый столбец – двойственной переменной уi (у1 = 3, у2 = 0, у3 = 5,5).
Определим отклонение в нижнюю сторону для ресурса Р1. Находим положительные элементы в первом столбце матрицы D. Это d21 = 0,4, соответствующий х2 = 920. Отсюда
![]() {x2/d21}
= 920/0,4 = 2300.
{x2/d21}
= 920/0,4 = 2300.
Определим отклонение в верхнюю сторону для ресурса Р1. Находим отрицательные элементы в первом столбце матрицы D. Это d21 = -0,3, соответствующий х1 =560 и d31 = -1,6, соответствующий х3 = 520.
Отсюда верхняя граница
Δb1+ = |max{xk/dk1}|=|max{-560/0,3; -520/1,6}|=|max{-1867; -325}| =|-325| = 325.
Таким образом, в интервале изменений запасов ресурса первого вида
b1
![]() {b1
-
{b1
-![]() ;
b1
+ Δb1+}
= {4800 - 2300; 4800 + 325} = {2500; 5125}
;
b1
+ Δb1+}
= {4800 - 2300; 4800 + 325} = {2500; 5125}
сохранится теневая (внутренняя) цена на этот вид ресурса у1*= 3 УДЕ.
Точно также найдем интервалы устойчивости у2* =0 и у3* =5,5 (УДЕ).
b2
{b2 -![]() ;
b2
+ Δb2+}
= {4200 - 520; 4200 + 0} = {3680; 4200};
;
b2
+ Δb2+}
= {4200 - 520; 4200 + 0} = {3680; 4200};
b3
{b3
-![]() ;
b3
+ Δb3+}
= {10000 - 1300; 10000 + 9200} = {8700; 19200}.
;
b3
+ Δb3+}
= {10000 - 1300; 10000 + 9200} = {8700; 19200}.
Изменение экстремального значения целевой функции исходной задачи при уменьшении объема каждого отдельно взятого ресурса на 100 УЕ считаем по Ш-ей теореме двойственности Z = bi · yi (i=1,2,3).
Для Р1 - Z b1 =-100 = 3 · (-100) = -300 (УДЕ); для Р2 - Z b2 =-100 = 0 – недефицитный вид ресурса; для Р3 - Z b3 = -100 = 5,5· (-100) = -550(УДЕ).
Ответы на вопросы:
Каждого вида продукции следует производить: П1= 0 (УЕ), П2= 560 (УЕ), П3 = 920 (УЕ), П4 = 0 (УЕ).
Ожидаемая максимальная выручка от продажи продукции составляет Zmax = 69400 (УДЕ).
Наиболее дефицитен ресурс Р3, наиболее убыточным является производство продукции вида П1.
Пределы устойчивости двойственных оценок к изменению запасов ресурсов: b1 {2500; 5125}; b2 {3680; 4200}; b3 {8700; 19200}.
Если запасы ресурсов каждого вида уменьшатся на 100 единиц, то максимальная выручка для Р1 – уменьшится на 300 УДЕ; для Р2 - останется без изменений и для Р3 - уменьшится на 550 УДЕ.
