54.? 55. Методика вывода формулы вычисления объёмов наклонного параллелепипеда и произвольной призмы. (53 см)

56.? 57. Методика введения понятий цилиндра, конуса, усеченного конуса и методика нахождения их площадей поверхностей и объёмов.

Общая характеристика:

Весь круг вопросов по этой теме можно условно разделить на 2 гр.

I. цилиндр и конус: а)опред.,поверхность,осев.сечен.,сеч.перпендик.оси; б)вписан. и описан.многогранники; в)объем; г)площ.боков.поверхн. При этом, разница изложения дан.материала состоит в порядке двух последн.пунктов. II. Шар и сфера: а)определение,сечен.плоскостью; б)объем шара; в)площадь сферы. Различен порядок изучения. Цилиндр и конус изучаются по единому плану. При изучении этих тел учитель должен подеркивать общее и различное при названии этих тел и их элементов(шир. Использовать методы сравнения, сопоставления и аналогий).

Сравнение учебников в трактовке опр. Ц. и К: а) по существу строгого определения этих понятий нет – лишь описание; б) во всех учебн.под цилиндром и конусом понимают геом.тело, т.е. ограничен.пространствен.область вместе с границей; в) Погорелов: цилиндр - тело, состоящее из двух кругов, не лежащих в одной плоскости и совмещаемых ||-ым переносом и всех отрезков, соедин-х соответствующие точки этих кругов. При этом вначале идет речь не о прямом круговом цилиндре, а о цилиндре общего вида(наклон.). однако, впоследствии делается оговорка: в дальнейшем будем рассматривать только прямой круговой цилиндр, для краткости назыв-ый просто цилиндр. Атанасян: перед описанием цилиндра, рассмат-ся цилиндрич.поверхности, а затем на основании этого делается описание цилиндра, кот., в отличие ото учебн.Погорелова, сразу выступает как прямой круговой цилиндр. Шлыков: цилиндр-тело,кот. образуется при вращении прямоугольника вокруг оси, содержащего его сторону. Аналогич.описывается и конус.

После описания Ц.и К. (или в процессе описания) вводятся понятия образующей, оси, основания, h, осевых сечений, S_{полн.пов.}, S_{бок.пов.}, вершины конуса и угла в осевом сечении К., касательной пл-ти. Во всех случаях целесообразно широко использовать модели, плакаты с рисунками тел и их элементов. Рассказать учащимся где в жизни всречаются такие формы( в быту и архитект.)

У Атанасяна

Понятие цилиндра вводится с его построения: окружность, проводят прямые перпендик-е пл-ти α, отрезки заключенные между α и β = цилиндрическая поверхность. Отрезки – образующие. Говорится о сходстве с параллельным переносом на в-р ОО1.

Есть чертеж цилиндра с указанием его частей.

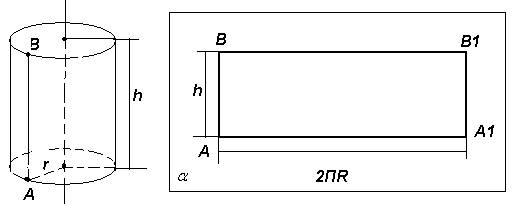
Тело, ограниченное цилиндрич. поверхностью и двумя кругами наз. цилиндром. Цилиндрич-я поверхность наз. боковой поверхностью, круги – основаниями. Образующие цилиндрич. пов-ти = образующие цилиндра. Длина образующей – высота цилиндра, радиус основания – радиус цилиндра. Осевое сечение – прямоугольник. Цилиндр получ-ся вращением прямоуг-ка.

Замечание: круговой наклонный цилиндр. Парабола- основание.

S поверхности цилиндра: разрезали и развернули. За площадь боковой поверхности цилиндра принимают площадь развёртки.

Т.к площадь прямоугольника AB*AA1=2пrh, то

Sбок=2πrh.

Площадь полной поверхности цилиндра – сумма площадей боковой поверхности и двух оснований.

Площадь каждого основания , тогда Sполн=2πr(r+h).

Конус – аналогично (коническая поверхность, вращаем прямоуг. треуг., развертка).

Тело, ограниченное коической поверхностью и кругом с грницей L, наз. конусом. Коническая поверхность наз. боковой поверхностью конуса, а круг – основанием конуса. Точку Р называется вершиной конуса, а образующие конической поверхности – образующими конуса. Осевое сечение –равнобедренный треугольник.

S= -площадь кругового сектора, 2πr= , Площадь боковой поверхности конуса равна произведению половины длинны окружности на образующую. Sбок=πrl,

Площадь полной поверхности конуса называется сумма площадей боковой поверхности и основания. Sполн=πr(l+r).

Далее усеченный конус, даются определения, получ. при вращении трапеции (прямоугольной).

Возьмём произвольный конус и проведём секущую плоскость, перпендикулярную его оси. Эта плоскость пересекается с конусом по кругу и разбивает конус на две части. Одна из частей представляет собой конус, а другая называется усечённым конусом.

Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую. Sбок=π(r+ r1)l (с выводом), l образующая.

У Погорелова Тела вращения.

Цилиндр – тело, кот. состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих точки этих кругов.

Конус – тело, которое состоит из круга – основание конуса, точки не лежащей в плоскости этого круга – вершина конуса и всех отрезков, соединяющих вершину с точками основания.

Далее идут определения как у Атанасяна. Определение конуса похоже на определение цилиндра. Вывод формул аналогичен.

Шлыков.

Цилиндр. Опр: Прямым круговым цилиндром или просто цилиндром наз геометрич-е тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, кот. перпендикулярны к образующим цилиндрич-й поверхности. + определение как у Атанасяна.

Определение равностороннего цилиндра (h=d). Далее все как у Атанасяна.

Опр: Круговым конусом наз. геометрич-е тело, ограниченное полостью конической поверхности и плоскостью перпендикулярной оси этой поверхности. Определения далее как у Атанасяна. Усеченный конус.

В цилиндр призму (правильную), в конус правильную пирамиду. У Погорелова все словами.