
6.3 Согласно принципу виртуальных перемещений
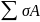 +
ф
=
0;
+
ф
=
0;
Qσx - a1* σх*В = 0;
а1 = Q/ В, = Q/ В,
Окончательный вид дифференциального уравнения движения системы:
В = Q
Задание 7.(уравнение Лагранжа)
Составить для данной механической системы уравнение Лагранжа.
Найти: закон изменения обобщенной координаты, считая, что состояние начинается из состояния покоя.
Уравнение Лагранжа – удобный алгоритм получения дифференциального уравнения.
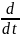 (
(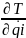 )
-
)
-
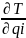 = Qi,
I
= 1,2…, p,
p
– число степеней своды системы.
= Qi,
I
= 1,2…, p,
p
– число степеней своды системы.
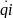 =
=
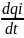 ,
обобщенная скорость.
,
обобщенная скорость.
Данная система имеет одну степень свободы р = 1, следовательно её положение определяется одной обобщенной координатой q. В качестве этой координаты выбрана координата х, характеризующая перемещение 1-го тела.
Для
него составим уравнение Лагранжа:
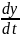 (
(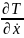 )
-
)
-
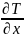 = Q.
= Q.
Т – кинетическая энергия системы,
Q – обобщенные силы,
- полная производная,
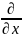 – частная
производная.
– частная
производная.
1) Т = В*V12 = В* 2;
2)
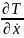 =
В*
=
В*
= В*
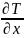 =
0;
=
0;
3) левая часть уравнения примет вид: В ;
4)
σх, σА =
 = Qσх;
= Qσх;
5) подставив полученные ворожения, подставим в дифференциальное уравнение Лагранжа, получим окончательное уравнение: В = Q.
Сравнив полученный результат с результатом 3-го и 6-го заданий, результат одинаковый, это доказывает мы получили уравнение движения системы тремя различными способами.
