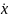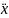Воронежский Государственный Технический Университет
Кафедра: Теоретической и прикладной механики.
РГЗ
По теоретической механике
Раздел: механика.
Вариант: 4
Выполнил:
Студент группы АО – 101
Бакуменко А. В.
Принял:
Доцент кафедры Т и МП
Бестужева Н. П.
Воронеж 2012 г.
Описание механической системы.
Механическая система состоит из: груза (1), сплошного цилиндрического катка (1), ступенчатых шкивов (2) с радиусами R и r. Массу считать равномерно распределенной по его ободу.
Звенья соединены нитями, намотанными на шкив.
Таблица 1. Исходные данные.
m1 , кг |
m2 , кг |
m3 , кг |
m4 , кг |
M , н*м |
S1 , м |
R2 , м |
r2 , м |
R3 , м |
r3 , м |
R4, м |
Угол α0 |
12 |
2 |
4 |
2 |
0,6 |
0,8 |
0,3 |
0,1 |
0,3 |
0,1 |
- |
30 |
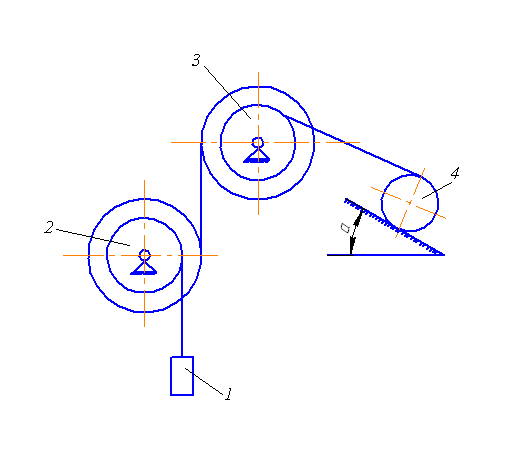
Рис. 1. Схема механизма.
Задание 1. Статика.
Необходимо произвести анализ сил, действующих на механизм, учитывая силы тяжести каждого звена, постоянный крутящий момент М и внешние реакции связей.
Найти: натяжение нити между 1 и 2 телом в случаи равновесия системы, используя условие равновесия груза 1.
Необходимые значения берутся из таблицы 1.
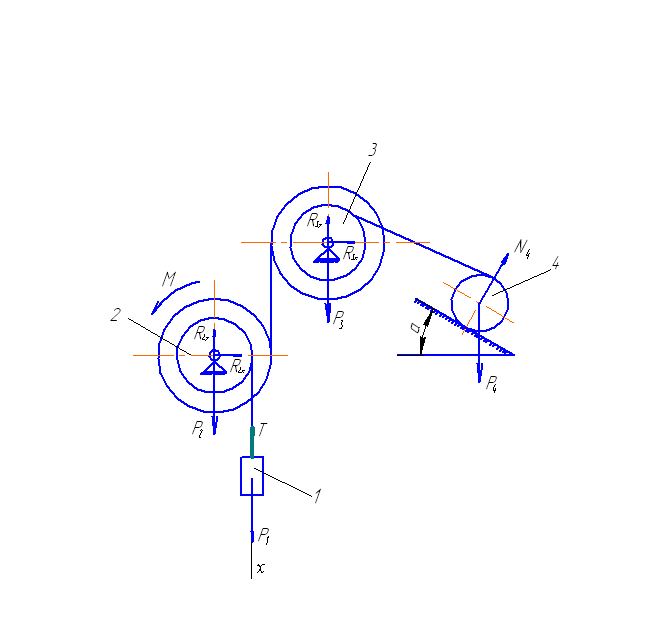
Рис. 2.
{Р1; Р2; Р3; Р4; R2х; R2у; R3х; R3у; Т; N4; М}
Так как груз свободно подвешен, то сила трения отсутствует.
За обобщенную координату принимаем координату х.
Р1 = m1 + g; Р2 = m2 + g; Р3 = m3 + g ; Р4 = m4 + g ;
В случаи равновесия системы:
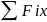 =
0;
=
0;
T
= Р1*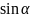 –
f
Р1*
–
f
Р1*
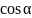 ;
так как α
= 90ْ
то
= 1 , cosα
= 0
;
так как α
= 90ْ
то
= 1 , cosα
= 0
Т = Р1; Т = 120 (н)
Задание 2. Кинематика.
Считая, что в данный момент времени скорость первого тела V1,
Выразить:
- скорость тел, совершающих поступательное движение;
- угловые скорости 2, 3, 4 звеньев и скорость центра масс 4 звена, через V1;
- угловые ускорения 2, 3, 4 и ускорении центра масс 4 звена, через а1;
- смещение всех звеньев, через смещение первого тела S1;
Необходимые значения берутся из таблицы 1.
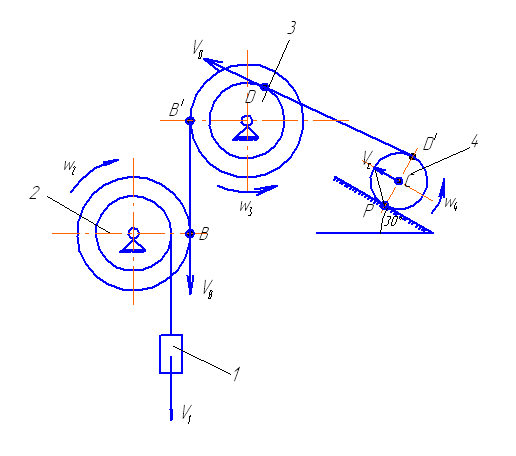
Рис. 3.
Механизм с одной степенью свободы.
Так как тела 2, 3 и 4 совершают вращательное движение связь между ω и Vимеет вид:
ω = V/R; V- скорость тела, R- радиус шкива(кратчайшее расстояние до ось вращения).
От
суда вытекает соотношение V
= ω
*R;
V
=
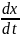 = x˙
= x˙
ω2
=
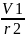 ;
;
VB
=
ω2*
R2;
ω3
=
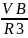 =
=
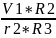 ;
;
Скорость точки С найдём с помощью мгновенного центра скоростей (МЦС) Р. Угловая скорость 4-го звена будет равна, угловой скорости точки С.
VD
=
ω3*
r3
=
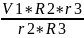 ;
ω4
=
;
ω4
=
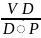 =
=
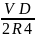 =
=
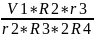 ;
;
Скорость точки С найдём с помощью мгновенного центра скоростей (МЦС) Р. Угловая скорость 4-го звена будет равна, угловой скорости точки С.
Vс
=
ω4*
CP
= ω4*
R4
=
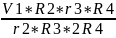 =
=
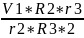 ;
;
Связь между скоростью и обобщенной координатой Х, позволяет выразить связи между конечными смещениями S1 и φ через обобщенную координату.
V1 | a1 = V1˙
ω2; ω3; ω4; | ε2 = ω2˙; ε3 = ω3˙; ε4 = ω4˙;
Vс | ас = Vс˙
Таблица 2. Связь между скоростями.
V1 |
ω2 |
ω3 |
ω4 |
Vс |
|
|
|
|
|
Таблица 3. Связь между ускорениями.
а1 |
ε2 |
ε3 |
ε4 |
ас |
|
|
|
|
|
Таблица 4. Связь между перемещениями.
S1 |
φ2 |
φ3 |
φ4 |
Sс |
х |
|
|
|
|
Таблица 5. Связь между виртуальными перемещениями.
σS1 |
σφ2 |
σφ3 |
σφ4 |
σSс |
σх |
|
|
|
|
Задание 3. Динамика.
Под действием сил тяжести система приходит в движение из состояния покоя. При движении на шкив 2 действует постоянный заданный крутящий момент М.
Найти:
- скорость 1-го тела V1 , в момент времени, когда его перемещении станет равно S1;
- ускорение 1-го тела а1;
- дифференциальное уравнение движения системы х(t);
Согласно теореме об изменении кинетической энергии
Т
– Т0
=
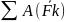
Так как по условию в начальный момент времени система находилась в покое, то Т0 = 0. Величина Т равна сумме энергии всех тел системы, исходя из этого выразим энергию через скорость V1.
Энергия системы примет вид:
Т = , Т = Т1+Т2+Т3+Т4;
Т1(пост)
=
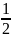 m1*
V12;
m1*
V12;
Т2(вращ) = I2* ω22, I2 = m2*R22, момент инерции 2-го тела, для 2-го шкива.
Т3(вращ) = I3* ω32, I3 = m3*R32, момент инерции 3-го тела, для 2-го шкива.
Т4(пл) = m4* Vс2 + I4* ω42, I4 = m4*R42, момент инерции 4-го тела, для однородного блока.
Т = m1* V12 + I2* ω22 + I3* ω32 + m4* Vс2 + I4* ω42;
Подставим значения моментов:
Т
=
m1*
V12
+
m2*R22*
ω22
+
m3*R32*
ω32
+
m4*
Vс2
+
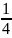 m4*R42*
ω42;
m4*R42*
ω42;
Подставим значение угловых скоростей и скорость 4-го звена:
Т = (m1* V12 + m2*R22*[ ]2 + m3*R32*[ ]2 + m4*[ ]2 + m4*R42*[ ]2;
Приведя подобные получим:
T = B* V12;
В
= m1
+
m2*[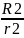 ]2
+ m3*[
]2
+ m3*[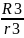 ]2
+ m4*[
]2
+ m4*[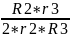 ]2
+
]2
+
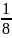 m4*[
m4*[ ]2;
B
= 66,75
]2;
B
= 66,75
Для
вычисления суммы работ внешних сил на
соответствующих перемещениях точек
системы
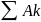 воспользуемся
анализом внешних сил (активных и реакций),
проведенных в задании 1. Работа постоянной
силы и крутящего момента вычисляется
по формулам:
воспользуемся
анализом внешних сил (активных и реакций),
проведенных в задании 1. Работа постоянной
силы и крутящего момента вычисляется
по формулам:
A(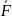 )
= Fs
)
= Fs ,
A(M) = ±M*φ.
,
A(M) = ±M*φ.
Где s – смещение точки приложения силы; χ = const – угол между векторами F и V, считается постоянным; φ – угол поворота тела.
Работа, совершаемая системой:
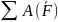 =
А(Р1)
+ А(М) + А(Р4);
выразим работы через смещение.
=
А(Р1)
+ А(М) + А(Р4);
выразим работы через смещение.
=
P1*S1
–
M*φ2
+ P4*Sc*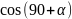 =
P1*S1
–
M*
+ P4*
=
P1*S1
–
M*
+ P4*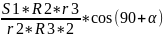 =
=
=
S1(P1
-
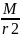 –
–
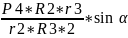 );
);
Сумма работ может быть записана в виде:
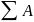 =
Q*S1;
=
Q*S1;
Q = P1 - – ; Q = 104 Учитывая, что Q и В const; Т0 = 0, получим:
В*V12 = Q*S1; (1)
В*V12 = 2*Q*S1;
V1
=
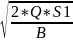 ;
;
Взяв за основу уравнение 1 выразим перемещение S1 через х, получим:
В*V12 = Q*х; продифференцируем по времени
В*
V1*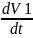 = Q*
= Q*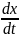 ,
так как
= а1,
= V1
уравнение
примет вид:
,
так как
= а1,
= V1
уравнение
примет вид:
В*а1 = Q;
а1
=
 а1
=
1,55 (м/с2)
а1
=
1,55 (м/с2)
=
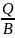
=
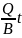 + C1
+ C1
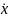 (0)
=
0; (из условия задачи)
(0)
=
0; (из условия задачи)
х
=
 t2
+ C1t
+ C2
x(0)
= 0; (из условия задачи)
t2
+ C1t
+ C2
x(0)
= 0; (из условия задачи)
В результате С1 = 0 и С2 = 0. Окончательный закон движения примет вид: х(t) = t2.