Решение разностных уравнений. Рекуррентный способ решения.

Рекуррентное решение может быть получено непосредственно из разностного уравнения.

Разрешим уравнение относительно координаты в момент .

Рекуррентное решение позволяет по известным прошлым значениям координат вычислить последующие значения. Т.е. задавая мы можем последовательно получать точки решения.

Достоинство: простота получаемых решений.

Недостатки: не получаем решение в виде формулы.

Пример:

Н

.у.:

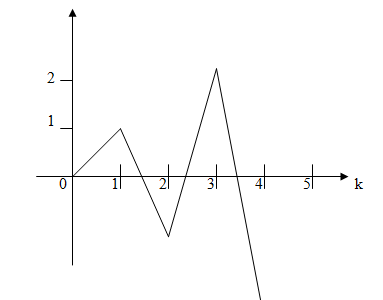
Лекция 4

Общие решения однородного разностного уравнения.

Решение однородного разностного уравнении имеет вид:

Введем оператор сдвига (решение сдвигается на единицу)

В символьном виде:

Для того, что бы лямбда в степ к, являлась решением ОРУ, необходимо что бы являлась корнем уравнения

Если корни кратные

Т.о. если знаем корни, знаем решение

Получение решения ОРУ:

1. составить характеристическое уравнение (оператор сдвига заменить на лямбда)

2. вычислить корни характеристического уравнения

3. записать общее решение с учетом простых и кратных корней

Пример:

Несложное разностное уравнение

Общее решение ОРУ

Виды решения при различных корнях

1 2 3 4 5

Корень действительный но отрицательный

1

1 2 3 4 5

- 1

Пара комплексно-сопряженных корней

>1 решения лежат на синусоиде

>1 решения лежат на синусоиде

Решение неоднородного разностного уравнения

Способы

1. Метод вариации производных постоянных

2. Метод стандартных функций и неопределенных коэффициентов для стандартных функций

Конкретные коэф частного реш получаются подстановкой частного решения в исходное разностного уравнения, затем приравнивание коэф при одинаковых функциях в левой и правой части уравнения.

3. Использование z-преобраз для решений ОРУ.

Р азностное уравнение

решаем

Обратное преобразование

Для использования этого метода необходимо:

1. От разностного уравнения перейти к его z-изображению и…..

X[k] ------x(z)

X[k+1] ------ z x(z)-z x[0]

Решение в области уравнений может быть получено

2. Решение в z-изображение

3. Вычислить обратное z-преобраз (может осуществляться разными способами – вычеты, ряд Лорана)

Если имеются ну, то они должны учитываться при изображении функций F[k+n]

В общем случае решение будет зависеть от вынуждающих функций и от нач условий

Пример:

Получить решение разностного уравнения

Перейдем к z-преобраз.

X[k] ------x(z)

X[k+1] ------ z x(z)-z x[0]

Физический смысл однородного и неоднородного разностного уравнения

Были начальные условия .потом воздействовала какая то сила, потом закончилась

­­­­

0 1 2 3 4 5 6 7 …

После прекращения вынуждающей силы, движение системы определяется решением однородного разностного уравнения, т.е. корнями характеристического уравнения. Устойчивость системы опред решением однородного разностного уравнения, а именно корнями характеристического уравнения.