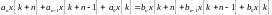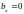Вычисление преобразования Лапласа импульсного сигнала по известному преобразованию Лапласа непрерывного сигнала.

_|_

Дискретные сигналы

Сигнал проходит через импульсный элемент.

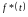- это импульсы

t

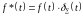
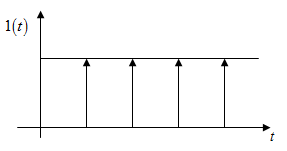
- это забор из единичных - импульсов.

t

Если его описать:

Возьмем преобразование Лапласа импульсного сигнала:

Функция

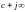
Р

Степень числителя 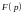на 2 порядка больше степени знаменателя, можно вычислить контурный интеграл.

Тогда преобразование Лапласа импульсного сигнала:

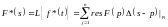
Рассмотрим два случая – если полюсы простые и если полюсы кратные.

1. Если - простой полюс.

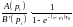
- вычет в простом полюсе

2. Если ; …… кратность

1. Вычисляется в скобках

2. Дифференцируется

3. Вычисляется значение полюса

Зная преобразование Лапласа непрерывного сигнала, можно определить преобразование Лапласа импульсного сигнала, что тоже, что и преобразование решетчатой функции. Т.е. фактически новая форма z-преобразования.

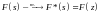
Если заменить 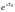на

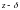
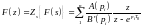- не только для простых полюсов

П

ример: Вычисление преобразования Лапласа импульсного сигнала.

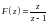- z-изображение решетчатой ступеньки

Решетчатые функции и их разности. Смещенная решетчатая функция.

Если есть непрерывный сигнал, то решетчатая функция - некоторая выборка.

Смещенная решетчатая функция

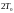
- фиксированный шаг квантования

Набирая смещенные решетчатые функции для разных значений можно полностью восстановить входной сигнал.

Конечная разность решетчатой функции.

1я разность:

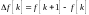
1 2 3 k

2я разность:

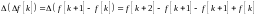
Разность любого порядка может быть выражена через значения решетчатой функции в смещенные моменты времени.

Конечная сумма – аналог интегрирования.

Конечная разность – аналог дифференцирования (неполный).

при стремлении , 1я разность стремится к значению производной умноженной на .

Понятия о разностных уравнениях.

Существует 2 формы разностных уравнений:

1. Непосредственно связанная с конечными разностями

2. 

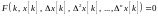
Начальный вектор (вектор начальных условий) определяется:

- н.у.

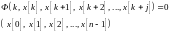
Линейные разностные уравнения с постоянными коэффициентами.

Порядок разностных уравнений и оператор сдвига

Введем символическую запись:

- ведение оператора дает сдвиг на шаг.

- сдвиг на m шагов квантования.

С учетом этого оператора перепишем уравнение:

Порядок уравнения определяется разностью между максимальным и минимальным показателем степени оператора сдвига .

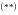Пример:

Разностное уравнение второго порядка.